Introduction
Approximate string matching, also called "string matching allowing errors", is the problem of finding a pattern p in a text T when a limited number k of differences is permitted between the pattern and its occurrences in the text.
Solutions
The oldest solution to the problem relies on dynamic programming. For example, see Levenstein distance implementation on Code Project (www.codeproject.com/KB/recipes/fuzzysearch.aspx) or in Wikipedia(http://en.wikipedia.org/wiki/Fuzzy_string_searching).
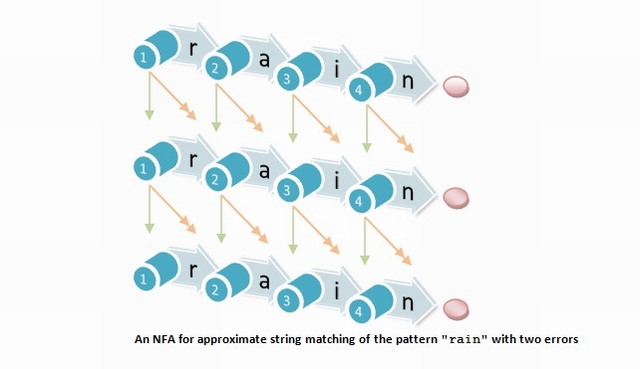
An alternative and very useful way to consider the approximate search problem is to model the search with a nondeterministic finite automaton (NFA). Consider the NFA for k = 2 errors. Every row denotes the number of errors seen. Every column represents matching a pattern prefix. Horizontal arrows represent matching a character (i.e., if the pattern and text characters match, we advance in the pattern and in the text). All the others increment the number of errors by moving to the next row: Vertical arrows insert a character in the pattern (we advance in the text but not in the pattern), short diagonal arrows substitute a character (we advance in the text and pattern), and long diagonal arrows delete a character of the pattern (they are e-transitions, since we advance in the pattern without advancing in the text). The initial self-loop allows an occurrence to start anywhere in the text. The automaton signals (the end of) an occurrence whenever a rightmost state is active.
BPR Algorithm
Bit-parallel algorithms are a simple and fast way to encode NFA states thanks to their higher locality of reference. Here is the pseudo-code for this algorithm that is described in the book "Flexible Pattern Matching in Strings" (see References for more information).
BPR (p = p1p2...pm, T = t1t2...tn, k)
1. Preprocessing
2. For c e S Do B[c] <- 0m
3. For j e 1 ... m Do B[pj] <- B[pj] | 0m-j10j-1
4. Searching
5. For i e 0 ... k Do Ri <- 0m-i1i
6. For pos e 1 ... n Do
7. oldR <- R0
8. newR <- ((oldR << 1) | 1) & B[tpos]
9. R0 <- newR
10. For i e 1 ... k Do
11. newR <- ((Ri << 1) & B[tpos]) | oldR | ((oldR | newR) << 1)
12. oldR <- Ri, Ri <- newR
13. End of for
14. If newR & 10m-1 <> 0 Then report an occurrence at pos
15. End of for
For example, let's search for pattern "rain" in "brain" text with 2 errors. We start with B=
r
| 0001
|
a
| 0010
|
i
| 0100
|
n
| 1000
|
*
| 0000
|
and { R0=0000 R1=0001 R2=0011 }. And here is step by step run:
b - 0000
R0- 0000
R1- 0000
R2- 0011
r - 0001
R0- 0001
R1- 0010
R2- 0100
a - 0010
R0- 0010
R1- 0111
R2- 1110
Occurrence at position 3
i - 0100
R0- 0100
R1- 1110
R2- 11111
Occurrence at position 4
n - 1000
R0- 1000
R1- 1100
R2- 1110
Occurrence at position 5
C# Implementation
public static void BPR(string pattern, string text, int errors)
{
int[] B = new int[ushort.MaxValue];
for (int i = 0; i < ushort.MaxValue; i++) B[i] = 0;
for (int i = 0; i < pattern.Length; i++)
{
B[(ushort)pattern[i]] |= 1 << i;
}
int[] states = new int[errors+1];
for(int i= 0; i <= errors; i++)
{
states[i] = (i == 0) ? 0 : (1 << (i - 1) | states[i-1]);
}
int oldR, newR;
int exitCriteria = 1 << pattern.Length -1;
for (int i = 0; i < text.Length; i++)
{
oldR = states[0];
newR = ((oldR << 1) | 1) & B[text[i]];
states[0] = newR;
for (int j = 1; j <= errors; j++)
{
newR = ((states[j] << 1) & B[text[i]]) | oldR | ((oldR | newR) << 1);
oldR = states[j];
states[j] = newR;
}
if ((newR & exitCriteria) != 0)
Console.WriteLine("Occurrence at position {0}", i+1);
}
}
References
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 










