Introduction
I started trying to develop a Sudoku solver in Excel using VBA. After a few interactions with Excel, I moved to Visual Basic using VS2005. After doing a version of the program
to deal with 9x9 (classic) Sudokus, I also adapted the code to solve Samurai Sudoku (5 overlapping 9x9 grids). I wanted to provide both a source and demo - as there aren't
too many fully featured solvers I could find in Visual Basic to learn from.
The logic based solvers and the UI probably took the most work - the actual brute force solver was actually pretty quick to code.
Terminology
This article doesn't go in depth into the rules of Sudoku or the detail of how to solve Sudoku puzzles. Just use a search engine if you want background on this.
However, the basic principle is that the numbers 1-9 are placed into the rows, columns, and subgrids so that every row, column, and subgrid only contain each digit once.
Some terms however are used below to explain the code.
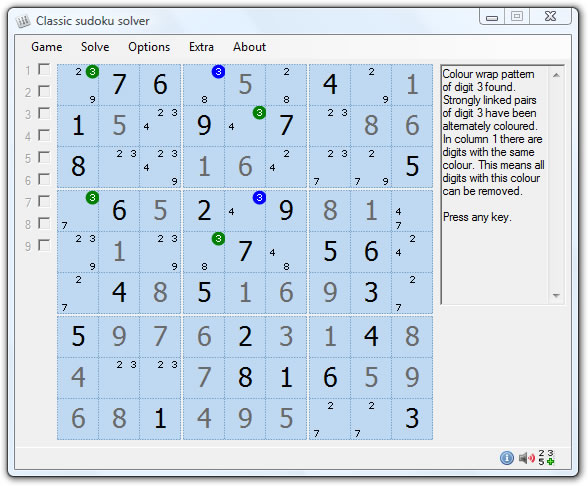
- Cell - individual cell where digits 1-9 can be placed.
- Clues/givens - in the first image above, the second and third cells hold clues of 7 and 6, respectively.
- Candidates/pencilmarks - in the image above, the first cell contains three candidates (2, 3, and 9). It is important when trying to solve a puzzle to keep track
of the various candidates.
- Row - a group of 9 cells going horizontally down the screen.
- Column - a group of 9 cells going vertically down the screen.
- Subgrid - a group of 9 cells arranged in a 3x3 grouping.
- Peers - in a 9x9 classic grid, each cell can 'see' up to 20 other cells (the other cells in the row, column, and subgrid). Due to the rule that
no digit can be repeated in a row, cell, or subgrid, if you place a digit as the solution to a cell, that digit can be removed as a candidate from each of its peers.
Peers for a Samurai Sudoku are a bit different, as some cells will have a greater number of peers due to the five overlapping grids.
Points of Interest
The solver will try to solve puzzles using logical steps, but will also resort to a brute force algorithm for tougher puzzles. Consequently, it can solve most
classic 9x9 Sudoku puzzles pretty much instantly, or most Samurai puzzles within a couple of seconds (depending on the computer). Admittedly, there are C++ solvers
that can solve hundreds or thousands of puzzles per second. However, I wanted something that would solve puzzles reasonably quickly, but also be able to step
through puzzles and show why particular solving steps were taken.
There is a custom control which uses GDI+ to paint clues and candidates (pencilmarks). Using a bunch of individual labels or the like was far too slow to refresh.
The UI can still be a little bit slow to refresh with Samurai puzzles, but is generally not too bad.
Unlike a lot of other solvers I've seen, which tend to use a two dimensional array of 81(9) to hold possible candidates for each cell, this solver uses a single array
of length 81 to hold all possible candidates. Each candidate is assigned a value using the formula 2 ^ (candidate-1) to come up with a unique bit value for each
candidate (although I've chosen to hard code this to minimise the need for this calculation). Therefore, candidate 1=bit value 1, candidate 2=bit value 2, candidate 3=bit value 4,
candidate 4=bit value 8, and candidate 5=bit value 16, and so forth.
So if cell 2 had candidates 1, 3, and 4 as possible values, you would set the value of the array to:
_vsCandidateAvailableBits(2) = 13 (bit values 1+4+8)
rather than having to do something like:
_vsCandidateAvailableBits(2,1) = True
_vsCandidateAvailableBits(2,3) = True
_vsCandidateAvailableBits(2,4) = True
The advantage of this approach is that a lot of logic based approaches to solving Sudoku work on subsets, so if you wanted to check if cell 81 only has candidates
1 and 9 available, it is trivial to do a simple check to see if _vsCandidateAvailableBits(81) = 257 (bit value 1 + bit value 256).
The actual solver itself is coded as a class and uses a depth first search. It will keep searching for multiple solutions, or can be set to exit after a set number of solutions are found.
Dim solver As New clsSudokuSolver
solver.intQuit = intSolverQuit
solver.blnClassic = True
solver.strGrid = strGame
solver.vsSolvers = My.Settings._DefaultSolvers
To run the solver, you need to call solver._vsUnique() which tests for a unique solution.
You can then do things like dim blnUnique as boolean = solver._vsUnique() to check see if a puzzle has a single valid solution or not.
Brute force solver
The brute force solver is held in its own class. It is basically an iterative loop that searches for a solution, by trying to find the best guess, and unwinding
guesses if they are incorrect.
The first task at hand is to load in the starting game (either a string holding 81 characters (for a 9x9 Sudoku) or five strings of 81 characters separated
by line breaks (for a Samurai Sudoku). Valid input are the characters 1-9 for starting clues and either a full stop or zero characters to represent unfilled/empty cells.
Private Function _load(ByVal strGrid As String, Optional ByVal _
StrCandidates As String = "") As Boolean
_vsSteps = 1
vsTried = 0
ReDim _vsUnsolvedCells(0)
Dim i As Integer
Dim intCellOffset As Integer
Dim strClues As String = ""
Dim g As Integer
Dim j As Integer
Dim intBit As Integer
Dim blnCandidates As Boolean = False
Dim arrCandidates() As String = Split(StrCandidates, arrDivider)
If arrCandidates.Length >= 81 Then blnCandidates = True
_u = -1
_vsCandidateCount(0) = -1
For i = 1 To _vsCandidateCount.Length - 1
_vsCandidateAvailableBits(i) = 511
_vsStoreCandidateBits(i) = 0
_vsCandidateCount(i) = -1
If blnClassic = False Then
If Not blnIgnoreSamurai(i) Then _vsCandidateCount(i) = 9
Else
_vsCandidateCount(i) = 9
End If
_vsLastGuess(i) = 0
_vsCandidatePtr(i) = 1
_vsSolution(i - 1) = 0
_vsPeers(i) = 0
Next
strGrid = Trim(strGrid)
Dim midStr As String = ""
Dim ptr As Integer
Dim arrayPeers(0) As String
Dim intValue As Integer
Dim nextGuess As Integer = 0
Dim nextCandidate As Integer = 0
_vsUnsolvedCells(0) = New List(Of Integer)
Dim intMaxGrid As Integer = 5
If blnClassic Then intMaxGrid = 1
For g = 1 To intMaxGrid
For i = 1 To 81
Select Case blnClassic
Case True
midStr = Mid(strGrid, i, 1)
intCellOffset = i
Case False
midStr = Mid(strGrid, i + (81 * (g - 1)), 1)
intCellOffset = intSamuraiOffset(i, g)
End Select
Select Case Asc(midStr)
Case 46, 48
If (blnClassic Or Not blnIgnoreSamurai(intCellOffset)) _
AndAlso _vsUnsolvedCells(0).IndexOf(intCellOffset) = -1 Then
_u += 1
_vsUnsolvedCells(0).Add(intCellOffset)
If blnCandidates = True Then
_vsCandidateAvailableBits(intCellOffset) = _
arrCandidates(intCellOffset - 1)
_vsCandidateCount(intCellOffset) = _
intCountBits(arrCandidates(intCellOffset - 1))
End If
End If
Case 49 To 57
intValue = CInt(midStr)
intBit = intGetBit(intValue)
If _vsSolution(intCellOffset - 1) = 0 Then
_vsSolution(intCellOffset - 1) = intValue
_vsCandidateCount(intCellOffset) = -1
If blnCandidates = False Then
Select Case blnClassic
Case True
arrayPeers = arrPeers(intCellOffset)
Case False
arrayPeers = ArrSamuraiPeers(intCellOffset)
End Select
For j = 0 To UBound(arrayPeers)
ptr = arrayPeers(j)
If _vsCandidateAvailableBits(ptr) And intBit Then
_vsCandidateAvailableBits(ptr) -= intBit
_vsCandidateCount(ptr) -= 1
End If
Next
End If
End If
Case Else
_load = False
Exit Function
End Select
strClues += midStr
Next
If Not blnClassic Then strClues += vbCrLf
Next
_load = True
strFormatClues = strClues
End Function
Once we have some valid input, we call a function that will loop to test for all solutions (although it is possible to set a value (intQuit) to exit when a desired
number of solutions have been found). For example, if you want to ensure a puzzle is valid (e.g., only has a single unique solution), then intQuit can be set to '2' (so it will exit
after finding two solutions). However, there can be instances (such as explained further below) where finding multiple solutions can be useful for solving Samurai puzzles.
The main solving function is set out below.
Private Function _vsbackTrack(ByVal strGrid As String, _
ByRef StrSolution As String, Optional ByVal _
StrCandidates As String = "") As Boolean
Dim intMax As Integer = 0
Dim intSolutionMax As Integer = 0
ReDim Solutions(0)
Dim i As Integer
Dim j As Integer
Dim intSolutions As Integer
Dim testPeers(0) As String
Dim tempPeers As String
Dim nextGuess As Integer = 0
Dim nextCandidate As Integer = 0
Select Case blnClassic
Case True
intMax = 81
intSolutionMax = 80
Case False
intMax = 441
intSolutionMax = 440
End Select
ReDim _vsSolution(intSolutionMax)
ReDim _vsPeers(intMax)
ReDim _vsCandidateCount(intMax)
ReDim _vsCandidateAvailableBits(intMax)
ReDim _vsCandidatePtr(intMax)
ReDim _vsLastGuess(intMax)
ReDim _vsStoreCandidateBits(intMax)
ReDim _vsRemovePeers(intMax)
If Not _load(strGrid:=strGrid, StrCandidates:=StrCandidates) Then
intCountSolutions = intSolutions
Exit Function
End If
_vsUnsolvedCells(0).Sort()
For i = 0 To _u
tempPeers = ""
Select Case blnClassic
Case True
testPeers = arrPeers(_vsUnsolvedCells(0).Item(i))
Case False
testPeers = ArrSamuraiPeers(_vsUnsolvedCells(0).Item(i))
End Select
For j = 0 To UBound(testPeers)
If _vsUnsolvedCells(0).IndexOf(CInt(testPeers(j))) > -1 Then
If tempPeers = "" Then
tempPeers = testPeers(j)
Else
tempPeers += "," & testPeers(j)
End If
End If
Next
_vsPeers(_vsUnsolvedCells(0).Item(i)) = tempPeers
Next
If _u = -1 Then
Exit Function
End If
While _vsSteps <= _u + 1 AndAlso _vsSteps > 0
If nextGuess = 0 Then nextGuess = intFindCell()
If nextGuess > 0 Then
nextCandidate = IntNextCandidate(nextGuess)
If nextCandidate > 0 Then
vsTried += 1
MakeGuess(nextGuess, nextCandidate)
nextGuess = 0
Else
If _vsSteps <= 1 Then
Select Case intSolutions
Case 0
_vsbackTrack = False
intCountSolutions = 0
Exit Function
Case 1
_vsbackTrack = True
intCountSolutions = 1
Exit Function
Case Else
_vsbackTrack = False
intCountSolutions = intSolutions
Exit Function
End Select
Else
UndoGuess(nextGuess)
End If
End If
Else
If _vsSteps = 0 Then
_vsbackTrack = False
intCountSolutions = intSolutions
Exit Function
Else
UndoGuess()
End If
End If
If _vsSteps > _u + 1 Then
intSolutions += 1
ReDim Preserve Solutions(intSolutions - 1)
Select Case blnClassic
Case True
StrSolution = strWriteSolution(intGrid:=1)
Case False
StrSolution = strWriteSolution()
End Select
Solutions(intSolutions - 1) = StrSolution
If intSolutions = intQuit Then
_vsbackTrack = False
intCountSolutions = intSolutions
Exit Function
End If
UndoGuess()
End If
End While
End Function
A key part of the brute force solver is doing a 'look ahead' to try to pick the next best unfilled cell to try placing an available candidate. The function below aims to do this
by looking for an empty cell with the minimum number of candidates available. If there is a cell with only a single candidate, this is selected, as this is an optimal guess.
Otherwise, the intention is to look for an unfilled cell with the smallest number of candidates (as this reduces the overall search space/solving time). As an additional refinement,
if there are multiple unfilled cells each with the same number of candidates, an additional loop is used to determine which of these cells has the highest number of peers (on the basis
that any guess made will have the highest chance of removing further candidates from the puzzle). There may be other approaches that can be trialed, as finding the best possible
next move is most likely to increase the solving speed.
Private Function intFindCell() As Integer
Dim i As Integer
Dim j As Integer
Dim ptr As Integer
Dim ptr2 As Integer
Dim arrPeers() As String
Dim intCell As Integer
Dim intCount As Integer
Dim intPeerCount As Integer
For i = 0 To 9
ptr = Array.IndexOf(_vsCandidateCount, i)
If ptr > -1 Then
intFindCell = ptr
If i = 0 Then
intFindCell = 0
End If
If i = 1 Then Exit Function
While ptr2 > -1
ptr2 = Array.IndexOf(_vsCandidateCount, i, ptr2)
If ptr2 > -1 Then
arrPeers = Split(_vsPeers(ptr2), arrDivider)
intPeerCount = 0
For j = 0 To UBound(arrPeers)
If arrPeers(j) <> "" AndAlso _
_vsUnsolvedCells(0).IndexOf(arrPeers(j)) > -1 Then
intPeerCount += 1
End If
Next
If intPeerCount >= intCount Then
intCount = intPeerCount
intCell = ptr2
End If
ptr2 += 1
End If
End While
intFindCell = intCell
Exit For
End If
Next
End Function
Once an unfilled cell has been selected, the next step is to find the next available candidate in that cell, as detailed below:
Private Function IntNextCandidate(ByVal intCell As Integer, _
Optional ByVal blnLookup As Boolean = False) As Integer
Dim c As Integer
Dim intBit As Integer
For c = _vsCandidatePtr(intCell) To 9
intBit = intGetBit(c)
If _vsCandidateAvailableBits(intCell) And intBit Then
IntNextCandidate = c
If blnLookup = False Then _vsCandidatePtr(intCell) = c + 1
Exit Function
End If
Next
End Function
The other main items required are functions to make guesses and wind back guesses, respectively. A key issue is keep track of where candidates have been removed from
the peers of a cell as the result of a guess. Without accurately recording this, it is not possible to properly undo guesses as required.
Private Function MakeGuess(ByVal intCell As Integer, _
ByVal intCandidate As Integer) As Boolean
Dim arrayPeers() As String
Dim j As Integer
Dim ptr As Integer
Dim intBit As Integer
_vsSolution(intCell - 1) = intCandidate
_vsCandidateCount(intCell) = -1
_vsLastGuess(_vsSteps) = intCell
_vsUnsolvedCells(0).Remove(intCell)
setCandidates(intCell, intCandidate)
_vsSteps += 1
arrayPeers = Split(_vsPeers(intCell), ",")
_vsRemovePeers(intCell) = New List(Of Integer)
intBit = intGetBit(intCandidate)
For j = 0 To UBound(arrayPeers)
ptr = arrayPeers(j)
If _vsSolution(ptr - 1) = 0 AndAlso _
(_vsCandidateAvailableBits(ptr) And intBit) Then
_vsCandidateAvailableBits(ptr) -= intBit
_vsCandidateCount(ptr) -= 1
_vsRemovePeers(intCell).Add(ptr)
If _vsCandidateCount(ptr) = 0 Then Exit Function
End If
Next
End Function
Private Function UndoGuess(Optional ByRef nextGuess As Integer = 0) As Boolean
Dim intCell As Integer = 0
Dim intCandidate As Integer = 0
Dim blnLoop As Boolean = True
_vsCandidatePtr(nextGuess) = 1
_vsSteps -= 1
If _vsSteps = 0 Then Exit Function
intCell = _vsLastGuess(_vsSteps)
intCandidate = _vsSolution(intCell - 1)
_vsUnsolvedCells(0).Add(intCell)
_vsUnsolvedCells(0).Sort()
Dim j As Integer
Dim i As Integer = 1
Dim c As Integer
Dim tC As Integer
Dim intBit As Integer = intGetBit(intCandidate)
Dim lbit As Integer = 0
If intCell > 0 Then
If Not (_vsStoreCandidateBits(intCell) And intBit) Then
_vsStoreCandidateBits(intCell) += intBit
End If
End If
lbit = _vsStoreCandidateBits(intCell)
_vsCandidateAvailableBits(intCell) = 0
For c = 1 To 9
intBit = intGetBit(c)
If lbit And intBit Then
_vsCandidateAvailableBits(intCell) += intBit
tC += 1
End If
Next
nextGuess = intCell
_vsSolution(intCell - 1) = 0
_vsCandidateCount(intCell) = tC
If intCell = 0 Then
Exit Function
End If
Dim pCell As Integer
For j = 0 To _vsRemovePeers(intCell).Count - 1
pCell = _vsRemovePeers(intCell).Item(j)
_vsCandidateAvailableBits(pCell) += intGetBit(intCandidate)
_vsCandidateCount(pCell) += 1
Next
End Function
Bruteforce - Samurai Puzzles
All Sudoku puzzles are considered NP-complete. In short, as the size of the grid increases, so does the potential time/computational effort to find a solution.
For Samurai puzzles, where there are five overlapping grids, it is unfortunately not just a matter of individually solving each of the five 9x9 grids in turn,
as it is usually the case that few or none of the individual grids taken in isolation have a unique solution - you usually need to solve all five overlapping grids as a single puzzle.
However, the code below is used to help reduce the solving time for harder Samurai puzzles. It basically involves testing to see if more than 1 but less than
100 solutions to an individual 9x9 grid can be found. Obviously, this won't always work, as there are often more than 100 solutions for an individual grid.
However, if there are less than 100 solutions, the collection of solutions is checked. If an empty cell has exactly the same digit appearing in each and every solution found,
we can then place that digit as this must be the correct answer for that cell.
If _u > -1 Then
If Not blnClassic Then
Dim g As Integer
For g = 1 To 5
Dim Solver As New clsSudokuSolver
Solver.blnClassic = True
Solver.strGrid = strWriteSolution(intGrid:=g)
Solver.vsSolvers = My.Settings._UniqueSolvers
Solver.intQuit = 100
Solver._vsUnique()
If Solver.intCountSolutions > 1 _
AndAlso Solver.intCountSolutions < Solver.intQuit Then
Dim s As Integer
Dim c As Integer
Dim m(81) As Integer
Dim chk(81) As Boolean
Dim chr As String
Dim intChr As Integer
For c = 1 To 81
chk(c) = True
Next
For s = 0 To UBound(Solver.Solutions)
If Array.IndexOf(chk, True) = -1 Then Exit For
For c = 1 To 81
chr = Mid(Solver.Solutions(s), c, 1)
intChr = CInt(chr)
If m(c) = 0 Then
m(c) = intChr
Else
If intChr <> m(c) Then
chk(c) = False
m(c) = -1
End If
End If
Next
Next
Dim strRevised As String = ""
Dim blnRevised As Boolean
Dim ptr As Integer
Dim arrayPeers() As String
Dim intBit As Integer
For c = 1 To 81
chr = Mid(Solver.strGrid, c, 1)
If chr = "." Then
If m(c) > 0 Then
strRevised += CStr(m(c))
blnRevised = True
ptr = intSamuraiOffset(c, g)
If _vsSolution(ptr - 1) = 0 Then
_vsSolution(ptr - 1) = m(c)
_vsCandidateCount(ptr) = -1
_vsUnsolvedCells(0).Remove(ptr)
arrayPeers = ArrSamuraiPeers(ptr)
intBit = intGetBit(m(c))
For j = 0 To UBound(arrayPeers)
If _vsSolution(arrayPeers(j) - 1) = 0 _
AndAlso (_vsCandidateAvailableBits(arrayPeers(j)) _
And intBit) Then
_vsCandidateAvailableBits(arrayPeers(j)) -= intBit
_vsCandidateCount(arrayPeers(j)) -= 1
End If
Next
_u -= 1
End If
Else
strRevised += chr
End If
Else
strRevised += chr
End If
Next
If blnRevised Then
blnRevised = False
End If
End If
Next
End If
End If
Generating Puzzles
Another thing I wanted to ensure was that I could generate Sudoku puzzles of different difficulties. I initially just tried starting with filled grids
and randomly removing digits...but this simply resulted in lots of easy puzzles, but very few difficult ones. The code below seems to help give a better range
of generated puzzles. The code below can be used to still result in a certain randomness in the deletion of clues from cells, but with the constraint that
a certain number of a particular digit will remain (e.g., it might delete 7 instances of the digit '8' and 6 instances of the digit '3', and the next time it might
delete 7 instances of the digit '2' and 6 instances of the digit '4', and so forth).
Function RemoveCellsNoSymmetry(ByVal strGrid As String) As String
Dim fp As Integer
Dim i As Integer
Dim j As Integer
Dim k As Integer
Dim p As Integer
Dim r As Integer
Dim r2 As Integer
Dim intRemoved As Integer
Dim strGeneratorSeed As String = "0122211000"
Dim randomArr() As String = _
Split(GenerateRandomStr(arrDivider), arrDivider)
Dim randomArr2() As String
Dim ptr As Integer
Dim arrGame(0) As Integer
Dim arrPos(0) As Integer
Dim midStr As String = ""
strGrid = Replace(strGrid, vbCrLf, "")
ReDim arrGame(81)
For p = 1 To 81
midStr = Mid(strGrid, p, 1)
ptr = p
If midStr <> "" AndAlso CInt(midStr) > 0 Then
arrGame(ptr) = CInt(midStr)
End If
Next
For i = 0 To 9
r = Mid(strGeneratorSeed, i + 1, 1)
For j = 1 To CInt(r)
Debug.Print(randomArr(k) & " will be found " & i & _
" times so delete " & 9 - i & " instances")
fp = -1
For p = 1 To 81
If arrGame(p) = randomArr(k) Then
fp += 1
ReDim Preserve arrPos(fp)
arrPos(fp) = p
End If
Next
intRemoved = 0
randomArr2 = Split(GenerateRandomStr(arrDivider), arrDivider)
For r2 = 0 To UBound(randomArr2)
If intRemoved >= (9 - i) Then Exit For
arrGame(arrPos(randomArr2(r2) - 1)) = 0
intRemoved += 1
Next
k += 1
Next
Next
RemoveCellsNoSymmetry = ""
For p = 1 To 81
ptr = p
If arrGame(ptr) <> "0" Then
RemoveCellsNoSymmetry += CStr(arrGame(ptr))
Else
RemoveCellsNoSymmetry += "."
End If
Next
End Function
Next Steps/Improvements
I wrote this mainly as a personal challenge. The key thing I'd like to do is improve the speed of the bruteforce solver, especially so it can solve Samurai puzzles
much more quickly, and improve the redraw speed so the GDI custom controls refresh faster. I might also do a version that will deal with other variants (such as jigsaw Sudoku puzzles).
Sample Application
The sample application is fully featured and lets you enter, solve, optmise, and generate classic (9x9) Sudoku puzzles and will let you enter and solve Samurai puzzles.
This member has not yet provided a Biography. Assume it's interesting and varied, and probably something to do with programming.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 










