Introduction
One of the most common tasks in statistics is computing the probability that a normal (Gaussian) random variable takes on a value between two bounds. This is used in computing interval estimates, constructing hypothesis tests, and making back-of-the-envelope estimates for many problems.
The SciPy numerical library for Python includes functions for computing such probabilities. However, SciPy does not work with IronPython at this time. This article will explain why some Python libraries work with IronPython and why some do not. Also, stand-alone code for computing normal probabilities is included that will work on any version of Python.
Background
The most common distribution in probability and statistics is the "normal" or Gaussian distribution. People often call this distribution "the bell curve." This distribution shows up everywhere: heights, IQ scores, measurement errors, etc.
A normal random variable has two parameters. The mean μ describes where the middle of the distribution is. The standard deviation σ describes how spread-out the distribution is. If X is a normal random variable with mean μ and standard deviation σ, the probability that X takes on a value between a and b is given by the integral below.
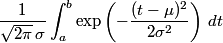
That integral cannot be computed in terms of simpler functions. Years ago people would look up values of the integral in books of tables. Of course now people use software instead of tables, and that's what this article is about.
At first it looks like we have a function of four variables: a, b, μ, and σ, but we can reduce the problem to computing a function of just one variable. First, we can assume μ = 0 and σ = 1. This is because if X is a normal random variable with mean μ and standard deviation σ, then Z = (X-μ)/σ is a normal random variable with mean 0 and standard deviation 1. So the probability P(a < X < b) equals the probability P((a-μ)/σ < Z < (b-μ)/σ. Also, we can assume b is -∞. This is because P(a < Z < b) = P(Z < b) - P(Z < a). So we've reduced the problem to needing to evaluate the following function.
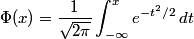
Numerical computing in (Iron)Python
Python does not include functions for computing the function Φ(z). However, the SciPy library includes an enormous collection of mathematical functions like Φ (Phi). ("SciPy" stands for "scientific Python.") The first place to go when looking for advanced math support in Python is SciPy. The code is well-tested and efficient (though not always well-documented).
The following example shows how to compute phi(0.7) from the Python command line using SciPy.
>>> from scipy.stats.distributions import norm
>>> norm.cdf(0.7)
0.75803634777692697
However, sometimes you might want to avoid creating an extra library dependence. For example, maybe you want to email somebody a quick Python script and don't want to assume they have SciPy installed.
Sometimes people can't use SciPy even if they want to. That's the case with IronPython.
IronPython is Microsoft's implementation of Python for .NET. IronPython let's you write Python syntax and access any .NET code. However, it doesn't always make it easy to call Python from .NET. In that sense, IronPython is a one-way gate: it makes easy for Python code to call .NET, but not necessarily for .NET code to call Python. The difficulty is with Python libraries, not with the Python language. Some Python libraries are implemented in C, and some are implemented in Python. A typical Python programmer doesn't need to be aware of the distinction, but an IronPython programmer does. IronPython can call code written in pure Python easily, but Python code implemented in C causes difficulties with .NET's managed code model. The Ironclad project addresses this problem. Also, folks from Microsoft have said that the situation should improve with future releases of .NET and the DLR (dynamic language runtime, the companion to .NET for dynamic languages such as IronPython and IronRuby).
Stand-alone Python code for Phi(x)
Here is a stand-alone Python implementation of the function Φ(x).
import math
def phi(x):
# constants
a1 = 0.254829592
a2 = -0.284496736
a3 = 1.421413741
a4 = -1.453152027
a5 = 1.061405429
p = 0.3275911
# Save the sign of x
sign = 1
if x < 0:
sign = -1
x = abs(x)/math.sqrt(2.0)
# A&S formula 7.1.26
t = 1.0/(1.0 + p*x)
y = 1.0 - (((((a5*t + a4)*t) + a3)*t + a2)*t + a1)*t*math.exp(-x*x)
return 0.5*(1.0 + sign*y)
The algorithm is based on formula 7.1.26 from Handbook of Mathematical Functions by Abramowitz and Stegun, affectionately known as "A&S." The algorithm given in A&S is for computing the error function erf(x). The error function is related to the the function Phi by a simple transformation. (The corresponding function in SciPy is scipy.special.erf.)
Because this code has no dependencies other than the standard math module, it should run anywhere Python runs. It has been tested on Python 2.5, Python 3.0, and IronPython. The code should be accurate to seven decimal places.
Now that we have an implementation of phi(x), we can write a simple wrapper around it to compute normal probabilities.
# Compute the probability that a normal(mu, sigma) random variable
# takes on a value between a and b.
def normal_probability(a, b, mu = 0, sigma = 1):
return phi((b-mu)/sigma) - phi((a-mu)/sigma)
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 





