Visual implementation of Graham's scan algorithm's data movement

• Download source - 185 KB
• Download demo - 66.1 KB

Introduction

The article shows you a visual implementation of Graham's scan algorithm's data movement to choose the smallest polygon.

Background

Graham's scan is a method of computing the convex hull of a finite set of points in the plane with time complexity O(n log n). It is named after Ronald Graham, who published the original algorithm in 1972.[1] The algorithm finds all vertices of the convex hull ordered along its boundary.

The first step in this algorithm is to find the point with the lowest y-coordinate.

Next, the set of points must be sorted in increasing order of the angle and the point P made with the x-axis.

The algorithm proceeds by considering each of the points in the sorted array in sequence. For each point, it is determined whether moving from the two previously considered points to this point is a "left turn" or a "right turn". If it is a "right turn", this means that the second-to-last point is not part of the convex hull and should be removed from consideration. This process is continued for as long as the set of the last three points is a "right turn". As soon as a "left turn" is encountered, the algorithm moves on to the next point in the sorted array.

Using the Code

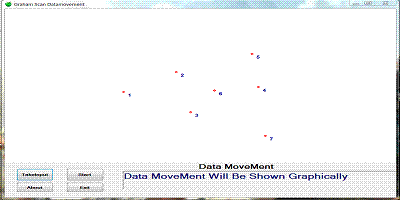
At first, we take input in a picturebox and show by drawing a point with the mouse.

//
// like this
//
private void button1_Click(object sender, EventArgs e)
{
    pictureBox1.BackColor = Color.White;
    signal = true;
}

private void pictureBox1_MouseClick(object sender, MouseEventArgs e)
{
    if (signal)
    {
        xcordinate[count] = e.X;
        ycordinate[count] = e.Y;
        
        
        Pen redPen = new Pen(Color.Red, 5);

        dc.DrawEllipse(redPen,e.X,e.Y,2,2);

        dc.DrawString(" "+(count+1), new Font("Arial", 10, FontStyle.Bold), 
           new SolidBrush(Color.DarkBlue), new Point(e.X+5,e.Y+5));

        pointName[count] = count + 1;
        count++;

    }
}
...

Then we can start our main processing by clicking the Start button.

private void button3_Click(object sender, EventArgs e)
{
    signal = false;
    button1.Enabled = false;

    //calculate smallesy Y
    findSnallestY();

    //Generate Angle array

    createAngleArray();

    //Sort angle array
    sortAngleArray();

    //find smallest polygon
    findSmallestPolygon();

    button3.Enabled = false;

    string final = " "+pointName[0];
    Point p;

    for (int i = 1; i < count; i++)
    {
        if (finalPointArray[i] == 1)
        {
            final = final + " , " + " " + " " + pointName[i] + " ";
        }
    }
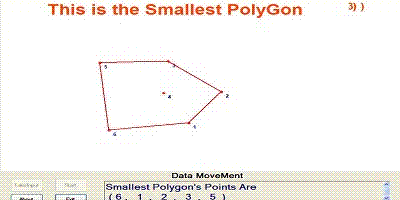
    richTextBox1.Text = "Smallest Polygon's Points Are \n" + " ("+final+ " )";
}

We follow these simple algorithm steps:

• First count the smallest Y
• Then create an angle array according to the small Y
• Then sort the angle array
• Then implement the algorithm

The main part is to find the smallest polygon. At first we take the first three points of the sorted point array based on the angle. Then we draw a line between the first two points.

int clockwise = 1;
int countclockwise = -1;
int l = 0,m = 1,i = 2;

finalPointArray = new int[count];

finalPointArray[l] = 1;
finalPointArray[m] = 1;
Pen redPen;
SolidBrush blueBrush = new SolidBrush(Color.White);

redPen = new Pen(Color.Red,2);

dc.DrawLine(redPen, new Point(xcordinate[0], ycordinate[0]), 
            new Point(xcordinate[1], ycordinate[1]));

Then we take the third point and calculate whether it is a right turn or left turn. If three points move at clockwise, then it is a right turn. Then we eliminate the middle point and also the line. Removing the line is simple, just draw the line again in white colour. After eliminating the point, we go one step back and calculate the turn with the other checked points. If three points make left turn, then we have to take the next point and calculate until all points are not traversed.

while(true)
{
    System.Threading.Thread.Sleep(2000);
    //if last point traversed
    if ((ccw(m, l, i) == clockwise) && (i == count-1 ))
    {
        finalPointArray[i] = 1;
        redPen = new Pen(Color.Red,2);

        dc.DrawLine(redPen, new Point(xcordinate[m], ycordinate[m]), 
                    new Point(xcordinate[i], ycordinate[i]));
        System.Threading.Thread.Sleep(2000);
        dc.DrawLine(redPen, new Point(xcordinate[i], ycordinate[i]), 
                    new Point(xcordinate[0], ycordinate[0]));
        string str = "";
        for (int j = 0; j < count ; j++)
        {
            if (finalPointArray[j] == 1)
            {
                str = str + "    " + Convert.ToString(j);
            }
        }

        redPen = new Pen(Color.White,2);
        dc.FillRectangle(blueBrush, 2, 2, 800, 70);
        redPen = new Pen(Color.Red,2);
        dc.DrawString("        This is the Smallest PolyGon", 
           new Font("Arial", 32, FontStyle.Bold), 
           new SolidBrush(Color.OrangeRed), new Point(2, 2));
           
        break;
    }

    //three points take left turn then draw two lines
    if (ccw(m, l, i) == clockwise)
    {
        dc.FillRectangle(blueBrush, 2, 2, 800, 70);
        redPen = new Pen(Color.Red, 2);
        dc.DrawString("LEFT TURN Between The points ( "+pointName[m]+" , 
          "+pointName[l]+" , "+pointName[i]+"  )", 
          new Font("Arial", 20, FontStyle.Bold), 
          new SolidBrush(Color.OrangeRed), new Point(250, 2));
        redPen = new Pen(Color.Red,2);

        dc.DrawLine(redPen, new Point(xcordinate[m], 
           ycordinate[m]), new Point(xcordinate[i], ycordinate[i]));
        
        finalPointArray[i] = 1;
        l = m;
        m = i;
        i++;
    }

    //if three points take right turn then remove
    //the line and middle point and move one step back
    else if (ccw(m, l, i) == countclockwise)
    {

        dc.FillRectangle(blueBrush, 2, 2, 800, 70);
        redPen = new Pen(Color.Red, 2);
        dc.DrawString("RIGHT TURN Between The Points ( " + pointName[m] + " , 
           " + pointName[l] + " , " + pointName[i]+"  )", 
           new Font("Arial", 20, FontStyle.Bold), 
           new SolidBrush(Color.OrangeRed), new Point(250, 2));

        redPen = new Pen(Color.Red, 2);
        dc.DrawLine(redPen, new Point(xcordinate[m], 
           ycordinate[m]), new Point(xcordinate[i], ycordinate[i]));
        System.Threading.Thread.Sleep(2000);
                    
        System.Threading.Thread.Sleep(2000);
        redPen = new Pen(Color.White, 2);
        dc.DrawLine(redPen, new Point(xcordinate[m], 
           ycordinate[m]), new Point(xcordinate[i], ycordinate[i]));
        dc.DrawString(" " + pointName[m], 
           new Font("Arial", 10, FontStyle.Bold), 
           new SolidBrush(Color.DarkBlue), 
           new Point(xcordinate[m]+5,ycordinate[m]+5));

        dc.DrawLine(redPen, new Point(xcordinate[l], 
           ycordinate[l]), new Point(xcordinate[m], ycordinate[m]));
        dc.DrawString(" " + pointName[l], 
           new Font("Arial", 10, FontStyle.Bold), 
           new SolidBrush(Color.DarkBlue), 
           new Point(xcordinate[l]+5, ycordinate[l]+5));
        redPen = new Pen(Color.Red, 2);


        dc.DrawEllipse(redPen, xcordinate[m], ycordinate[m], 2, 2);
        dc.DrawEllipse(redPen, xcordinate[l], ycordinate[l], 2, 2);
        dc.DrawEllipse(redPen, xcordinate[i], ycordinate[i], 2, 2);
        finalPointArray[m] = 0;
        m = l;
        l = letestBefore(l);
    }
}

Points of Interest

We can give all input at a time only. To determine the next polygon, we have to run the software again.

References

• Graham, R.L. (1972). An Efficient Algorithm for Determining the Convex Hull of a Finite Planar Set. Information Processing Letters 1, 132-133
• De Berg, Mark; Cheong, Otfried; Van Kreveld, Marc; Overmars (2008). Computational Geometry Algorithms and Applications. Berlin: Springer. pp. 2–14. doi:10.1007/978-3-540-77974-2. ISBN 978-3-540-77973-5.
• Berkman, Omer; Schieber, Baruch; Vishkin, Uzi (1993). "Optimal double logarithmic parallel algorithms based on finding all nearest smaller values". Journal of Algorithms 14 (3): 344–370. doi:10.1006/jagm.1993.1018.