One of the hats I wear at work is that of the performance analysis guy. I work at a multiplatform shop, so naturally, I have a vested interest in retaining technologies that can be reliably used on different platforms without too much fussing around, and Python was the logical choice. With minimal care taken, a Python script can be designed to run on any of the supported platforms from Andrioid to Windows. Further, dealing with different Python versions can also be dealt with dynamically at runtime as well.
Python, is SQLite3 ready right out of the box, and it’s desirable to use this combination to form a tool set for statistical processing common in performance analysis.
Unlike SQLite’s lustrous big brothers and sisters in the Enterprise Level Client-Server market, like Oracle, IBM DB2, Microsoft SQL Server, and MySQL, that offer a rich assortment of built in aggregates, SQLite offers just the basic aggregate functions like Average, Max, Min, Count, group_concat, Sum and Total. The more complex Statistical aggregate functions are sadly missing.
However, this is not an oversite on the part of the SQLite folks, but purposely designed into it. SQLite has been designed to have a small footprint, and in many applications, it is common place to be embedded in hardware, or resided in memory.
In my case, I need these statistical functions, especially Standard Deviation, as it’s the basis of a myriad computations.
Fortunately, SQLite allows the importing of custom aggregate functions, to the database at run time by means of the create_aggregate() method in what could be described as a kind of an à la carte fashion.
This is very advantageous as it allows for adding of custom adhoc functionality to the database without the need of the ugly paradigm of pulling, processing and pushing data back and forth, CPU intensive loops and iterations outside the data layer. Data functions are preformed intra-tier vs inter-tier The database can be thought of as a container object that processes data internally, that can be as smart as a whip, or as dumb as a post. The choice is yours based on your needs at runtime.
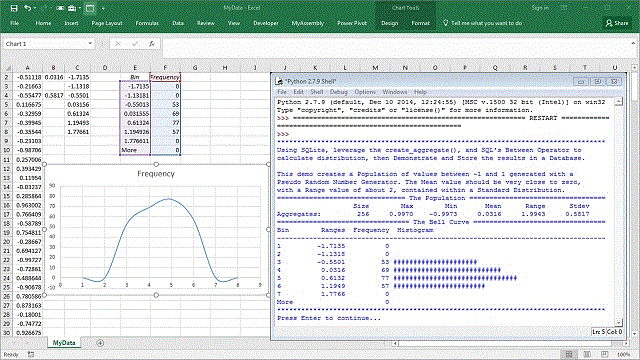
This script demonstrates the use of SQLite’s create_aggregate() as the base function to produce one of the most common Statistical Analysis tools, namely the distribution histogram, or what is more commonly referred to as a Bell Curve.
import sqlite3
import math
import random
import os
import sys
import traceback
import random
class StdevFunc:
def __init__(self):
self.M = 0.0
self.V = 0.0
self.S = 0.0
self.k = 1
def step(self, value):
try:
if value is None:
return None
tM = self.M
self.M += (value - tM) / self.k
self.V += (value - tM) * (value - self.M)
self.k += 1
except Exception as EXStep:
pass
return None
def finalize(self):
try:
if ((self.k - 1) < 3):
return None
self.V = (self.V / (self.k-2))
self.S = math.sqrt(self.V)
return self.S
except Exception as EXFinal:
pass
return None
def Histogram(Population):
try:
BinCount = 6
More = 0
con = sqlite3.connect(':memory:')
con.row_factory = sqlite3.Row
con.create_aggregate("Stdev", 1, StdevFunc)
cur = con.cursor()
cur.executescript('drop table
if exists MyData;')
cur.execute("create table IF NOT EXISTS MyData('Val' FLOAT)")
cur.executescript('drop table
if exists Bins;')
cur.execute("create table IF NOT EXISTS Bins('Bin'
UNSIGNED INTEGER, 'Val' FLOAT, 'Frequency' UNSIGNED BIG INT)")
for n in range(0,(Population)):
sql = "insert into MyData(Val) values ({0})".format(random.uniform(-1,1))
cur.execute(sql)
pass
cur.execute("select Avg(Val) from MyData")
Average = cur.fetchone()[0]
cur.execute("select Max(Val) from MyData")
Max = cur.fetchone()[0]
cur.execute("select Min(Val) from MyData")
Min = cur.fetchone()[0]
cur.execute("select Count(Val) from MyData")
Records = cur.fetchone()[0]
cur.execute("select Stdev(Val) from MyData")
Stdev = cur.fetchone()[0]
Range = float(abs(float(Max)-float(Min)))
if (Stdev == None):
print("================================ Data Error ===================================")
print(" Insufficient Population Size, Or Bad Data.")
print("**********************************************************************************")
elif (abs(Max-Min) == 0):
print("================================ Data Error ===================================")
print(" The entire Population Contains Identical values, Distribution Incalculable.")
print("**********************************************************************************")
else:
Bin = []
Frequency = []
being subtracted from the Mean
Bin.append(float((Average - ((3 * Stdev)))))
Frequency.append(0)
for b in range(0,(BinCount) + 1):
Bin.append((float(Bin[(b)]) + Stdev))
Frequency.append(0)
for b in range(0,(BinCount / 1) + 1):
right exclusive.
sqlBinFreq = "select count(*) as Frequency from MyData
where val between {0} and {1} and Val < {2}". \
format(float((Bin[b])), float(Bin[(b + 1)]), float(Bin[(b + 1)]))
Store the Frequency to a Bins Table.
for rowBinFreq in cur.execute(sqlBinFreq):
Frequency[(b + 1)] = rowBinFreq['Frequency']
sqlBinFreqInsert = "insert into Bins (Bin, Val, Frequency) values ({0}, {1}, {2})". \
format(b, float(Bin[b]), Frequency[(b)])
cur.execute(sqlBinFreqInsert)
More = (More + Frequency[b])
More = abs((Records - More))
sqlBinFreqInsert = "insert into Bins (Bin, Val, Frequency) values ({0}, {1}, {2})". \
format((BinCount + 1), float(0), More)
cur.execute(sqlBinFreqInsert)
print("================================ The Population ==================================")
print(" {0} {1} {2} {3} {4} {5}". \
format("Size".rjust(10, ' '), \
"Max".rjust(10, ' '), \
"Min".rjust(10, ' '), \
"Mean".rjust(10, ' '), \
"Range".rjust(10, ' '), \
"Stdev".rjust(10, ' ')))
print("Aggregates: {0:10d} {1:10.4f} {2:10.4f} {3:10.4f} {4:10.4f} {5:10.4f}". \
format(Population, Max, Min, Average, Range, Stdev))
print("================================= The Bell Curve =================================")
LabelString = "{0} {1} {2} {3}". \
format("Bin".ljust(8, ' '), \
"Ranges".rjust(8, ' '), \
"Frequency".rjust(8, ' '), \
"Histogram".rjust(6, ' '))
print(LabelString)
print("----------------------------------------------------------------------------------")
sqlChart = "select * from Bins order by Bin asc"
for rowChart in cur.execute(sqlChart):
if (rowChart['Bin'] == 7):
BinName = "More"
ChartString = "{0:<6} {1:<10} {2:10.0f}". \
format(BinName, \
"", \
More)
else:
BinName = (rowChart['Bin'] + 1)
fPercent = ((float(rowChart['Frequency']) / float(Records) * 100))
iPrecent = int(math.ceil(fPercent))
ChartString = "{0:<6} {1:10.4f} {2:10.0f} {3}". \
format(BinName, \
rowChart['Val'], \
rowChart['Frequency'], \
"".rjust(iPrecent, '#'))
print(ChartString)
print("**********************************************************************************")
con.commit()
cur.close()
con.close()
except Exception as EXBellCurve:
pass
TraceInfo = traceback.format_exc()
raise Exception(TraceInfo)
print("**********************************************************************************")
print("Using SQLite, leverage the create_aggregate(), and SQL's Between Operator to")
print("calculate distribution, then Demonstrate and Store the results in a Database.\n")
print("This demo creates a Population of values between -1 and 1 generated with a")
print("Pseudo Random Number Generator. The Mean value should be very close to zero,")
print("with a Range value of about 2, contained within a Standard Distribution.")
PythonVersion = sys.version_info[0]
Population = (16 ** 2)
Histogram(Population)
if (PythonVersion == 3):
kb = input("Press Enter to continue...")
else:
kb = raw_input("Press Enter to continue...")
A few words about the script.
The script will demonstrate adding a Standard Deviation function to a SQLite3 database. For demonstration purposes, the script will 1st run a Pseudo Random Number Generator to build a population of data to be analyzed.
This script has been tested on Windows, and Linux platforms, as well as Python 2.6, - 3.4.
A few words about the Bell Curve.
Since, distribution analysis is at the core what a Bell Curve speaks to, we will produce a population, of adequate size, with random seeded numbers ranging from -1 to 1. This will assure a Standard Distribution, and where results are easy to interpret.
Basically, if you produce a long series of numbers from -1 to 1, then the expectation would be for a population to produce a mean of close to 0, a range very close to 2. The result in essence simply displays just how random the Python Random Number Generator actually is.
There are no official Bin allocation rules for histograms. This demo utilizes Bin allocation rules based Excel’s Data Analysis Add-on, Histogram feature.
Download Script
https://support.microsoft.com/en-us/kb/213930
This member has not yet provided a Biography. Assume it's interesting and varied, and probably something to do with programming.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 










