Introduction
Checking if a line segment really crosses or is inside a polygon is always a hard geometric problem for programmers to solve. We can hardly find a general algorithm
for line segment-polygon intersection checking. My article is to suggest an idea for testing whether a line segment crosses a polygon or not, it can be applied for only
simple computer graphics polygons (including convex and concave ones).
Background
Conventions
The pseudo-code I am using in this article is a Java-like language. It is a mixture between structural programming and object oriented programming.
Suppose that point, line segments (from now on I will use 'segment'), and polygons are implemented with basic methods such as segment-segment intersection,
segment containing a point, polygon containing a point, length of a segment, midpoint…
Acknowledgements
A segment crosses a polygon if one of its parts crosses that polygon. A segment crosses a polygon if it cuts or is inside that polygon.
A segment cuts a polygon if it has at least one intersection that is not the end point of the segment. A segment is inside a polygon if every point
of the segment is inside the polygon (end points of the segment can lay on the boundary of the polygon). These edges of a polygon are not inside this polygon.


New Solution
Idea
Directly from the acknowledgements, we have these clauses:
- A segment crosses a polygon if it cuts or is inside that polygon.
- A segment is inside a polygon if every point of the segment is inside the polygon.
The conclusion is: if a part of the segment is inside the polygon, the segment crosses the polygon.
So, our work is to split the original segment into smaller parts in order to check if there is a part that is inside the polygon.
Which kind of segment can be inside a polygon?
If a segment is totally inside or outside a polygon, then it has no intersection with
the edges of the polygon (end points of the segment can lay on the boundary of the polygon).
We can determine only that kind of segment is inside/outside a polygon.

How to split a segment?
With each segment, we try to find its intersection with an edge of the checking polygon. If the intersection exists and is not an end point of this segment,
split the segment into two small parts, one is from Begin to the intersection, another from
the intersection to the End (Begin and End the end points of the segment).
Do these steps recursively until the segment has no intersection with the edges of the polygon.

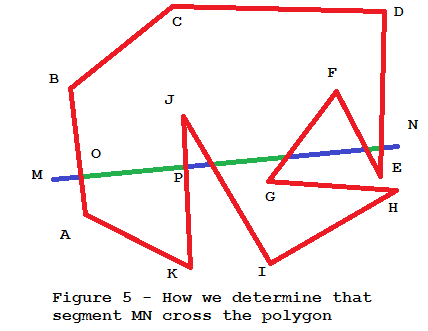
Figure 4 is a good example: Segment MN intersects edge AB and O is the intersection. We split MN into MO and ON.
Check if a part is inside a polygon
The segment s, that we are checking, is a small part of a big segment. The condition is "segment s and polygon p have no intersection" (it is OK if end points of segment s lay on the boundary of the polygon p).
If the part is an edge of the polygon, it is not inside. Otherwise, every point of the part is on the same side (end points can lay on the boundary of the polygon).
We can pick up an arbitrary point (I chose midpoint), the whole part will be on the same side to this point. Pseudo-code:
public boolean Cover(Polygon p, Segment s)
{
for (int i=0; i< p.Edges.count; i++)
if (s == p.Edges[i])
return false;
Point mid = s.MidPoint();
if (p.Contains(mid))
return true;
else
return false;
}
Check if a segment crosses a polygon
Step 1: Try to split the segment into two parts. If it is possible, go to step 2, otherwise go to step 4.
Step 2: Recursively check if the first part crosses the polygon. If it does not, go to step 3, otherwise the segment crosses the polygon. Stop the algorithm.
Step 3: Recursively check if the second part crosses the polygon. If it does not, the segment does not cross the polygon, otherwise the segment crosses the polygon. Stop the algorithm.
Step 4: Check if the segment is inside the polygon. If it is inside, the segment crosses the polygon, otherwise it does not. Stop the algorithm.
Pseudo-code:
public boolean Cross(Segment s, Polygon p) {
Point split_point = null;
for (int i=0; i< p.Edges.count; i++)
{
Segment edge = p.Edges[i];
split_point = s.InterSectionExceptThisEnds(edge);
if (split_point != null)
break;
}
if (split_point != null)
{
boolean first_part = Cross(new Segment(s.p1,split_point), p);
if (first_part == true)
return first_part;
boolean second_part = Cross(new Segment(split_point,s.p2), p);
return second_part;
}
else
{
boolean result = Cover (p, s);
return result;
}
}
Back to Figure 4 for an example. Let’s do it step by step.

- First, we split MN into MO and ON.
- Then we check MO. MO cannot be split and it is outside the polygon.
- So we have to check ON.
- ON can be split into OP and PN.
- OP cannot be split and it is inside the polygon.
- OP is a part of ON, so ON is crossing the polygon.
- ON is the second part of MN, then we determine that MN crosses the polygon.
Conclusion
This algorithm can check if a segment crosses a polygon, and the programmer can modify it to determine that
the segment is inside or cuts the polygon and gets the intersections if they exist.
Do not apply this to a complex polygon (a polygon that intersects itself or has holes in it). But programmers can separate
a self-intersecting polygon into some simple polygons
and determine holes as polygons, then apply and modify this algorithm for their own purposes. I used to spend a lot of time searching for
a geometric algorithm on the internet, which is time-consuming, so I am sharing my experience and hoping that it is helpful. I am waiting for positive comments to make the article better. Have fun.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 






 )
)
