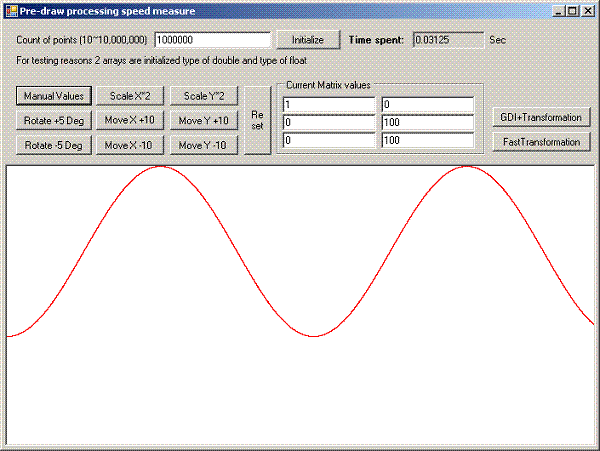
Introduction
Purpose of this article to prove that newest does not meat faster
or better, and that Assembler is still quite useful for time critical
code. Because user don't like to wait - drawing, and all operations
related to data pre-drawing processing should be done with super
sonic speed. But it is impossible to do anything with drawing itself,
and it does not matter what you are using for drawing GDI, GDI+,
Direct X or OpenGL. But it is possible to optimize pre-drawing data
processing. What I mean saying pre-drawing processing? Pre-drawing
processing includes next steps:
- Affine transformation
- Clipping
- Draw points simplification
So let's see what can be used for operation listed above from
standard .Net libraries.
- For affine transformation best
candidate is
System::Drawing::Drawing2d::Matrix. But
unfortunately it performs transformations too slow.
- For clipping operations I found
nothing.
System::Drawing::Graphics have the ClipBounds
property but if you try to draw some primitive with coordinates
specified too far from visible area, it will crash.
- For simplification there is also nothing provided in standard
libraries.
As result all pre-drawing operations it is the developers head pain, and in this article I will try to show how to minimize this
head pain.
Background
Let's see next task, as input we have a curve represented by huge
amount of points, let's say 1,000,000. And we need to perform this
curve drawing interactively. So all operations responsible for
preparing original curve for drawing should be done very quickly.
This pre-drawing operations includes all three operations mentioned
above in introduction paragraph. To solve this task, couple of
approaches can be assumed.
Create you own class Matrix to perform affine
transformations with high speed. Create functionality or class to
perform clipping. Create functionality or class to perform points
simplification. Of course this approach can be in line with OOP
ideology and universal, and will solve speed problem for each step.
But let's see disadvantages of this realization. Per each step memory
allocation for result storing is required, of course result of
current step will be used and input data for next step. So totally,
in worst case this realization will perform at least three memory
allocation operations, and in worst case run loop through all points
three times, so total time complexity will be O(3n).
I want to introduce may be not very universal and object oriented
approach but it does not have disadvantages of approach described
above. Main idea is to perform all pre-drawing operations in one
single loop, so per each loop iteration transformation, clipping and
simplification operations are performed. Also key point is to
performs memory reallocations as least as possible, and to access
memory as least as possible. Of course dynamic memory allocation is
good, but in other hand, it cause additional operation to look for
proper size memory block to allocate. So than less memory
(re)allocations in routine than better performance it can reach.
So let's see this approach in details. First class I want to introduce is managed <CODE>Transformer
class responsible for memory allocation to store result of
operations, and for interaction with unmanaged code. This class do
not perform by itself any operations, and do not need any information
about transformation matrix or about clipping area. This class can be
easily extended or modified to fit your needs, or to be included into
your project. Also because all data required for pre-drawing
operations are parameters of function call, it gives the flexibility
to end user of this class. Because you can use any matrix and any
clip bounds structures or classes you prefer.
Second thing to be introduced is a set of unmanaged functions
implemented in assembler language to perform affine transformations,
clipping, result points simplification and output. Key points of
implementation of this functions:
- Do not perform any dynamic memory allocations.
- Perform transformation, clipping
and simplification in one loop. So time complexity of implemented
algorithm is O(n).
- Reduced count of memory access
(far addressing in terms of assembler). This is quite important
factor for execution speed, because register access is times faster
than memory access. So per each iteration memory is accessed in
worst case only 4 times.
- Load current point to XMM
register. Thanks to SSE2 instructions it is possible just through
only one memory access.
- Write result point, Here thanks to MMX
instructions.
- Increment counter of result
points, because this value is located on the stack.
- Discontinuity marker set. (Only
if it is necessary).
- Another aspect of minimizing
memory access is that transformation matrix values and clip bounds
are loaded to xmm registers only ones before main loop. This is
quite important for execution time, because such kind of
optimization can not be done by compiler, and allows to reduce
memory access during loop iteration. If you write your code in C,
C++ or C# or any other high level programming language such kind of
optimization is impossible.
- Usage of MMX/SSE2/SSE3 instructions allows, as mentioned
above to cache data used per each iteration in mmx/xmm registers,
and also to improve speed of calculations and calculations accuracy.
Now is a time to take a closer look at main actors of algorithm.
In code samples below I will describe key points of implementation
and reasons why it is done this way. So code below is part of
TransfromClipReducePoints function and responsible for
initialization.
;load transformation matrix to xmm0-xmm2 registers in a way:
; register Low | High
;-------------------------
; xmm0 m00 | m10
; xmm1 m01 | m11
; xmm2 m20 | m21
movsd xmm0,_m00
movhpd xmm0,_m10
movsd xmm1, _m01
movhpd xmm1, _m11
movsd xmm2, _m20
movhpd xmm2, _m21
;loading clipping bounds to xmm6, xmm7 registers in a way
; register Low | High
;-------------------------
; xmm6 xMin | yMin
; xmm7 xMax | yMax
movsd xmm6, _xMin
movhpd xmm6, _yMin
movsd xmm7, _xMax
movhpd xmm7, _yMax
;discontinuity marker loading to mm7 register
mov eax, 80000000h
push eax
push eax
movq mm7, [esp]
add esp,8h
xor eax, eax
push eax ;stack allocation for output points count.
xor ebx, ebx ;initialization to store discontinuity flag.
Key points to be mentioned:
- Way of transformation matrix
loading.
Original matrix.
|
xmm0 Low
|
xmm0 High
|
xmm1 Low
|
xmm1 High
|
xmm2 Low
|
xmm2 High
|
|
m00
|
m10
|
m01
|
m11
|
m20
|
m21
|
How elements go to xmm registers.
Matrix loading is done in this way to reduce amount of operations
repeated per each point loading. Because data in input array are
located x0,y0,x1,y1,...xn,yn it is possible to load to xmm register
one point coordinates x,y per one memory access. And because matrix
is loaded to xmm registers in the way mentioned above,
it allows to load data as is, without additional recombination, for
calculation.
Discontinuity marker is a defined value of outputted point
coordinates to specify that curve goes out of clipping area. Value
80000000h corresponds to int::MinValue for
managed code. Marker value is stored at mm7 register to
be outputted per one memory access.
Next part of code performs affine transformation per each point.
;---------------------------------------------------------------------
;Function performs affine transformation of point located by ptr[esi]
;increments [esi] to point no next point
;calculated point is stored in xmm3 register, in a way Low - X, High-Y
;---------------------------------------------------------------------
TransformPoint PROC PRIVATE
movupd xmm3, [esi] ;xmm3 = x,y
movapd xmm4,xmm3 ;xmm4 = x,y
;Calculation
mulpd xmm3, xmm0 ;xmm3 = M00*X | M10*Y
mulpd xmm4, xmm1 ;xmm4 = M01*X | M11*Y
haddpd xmm3,xmm4 ;xmm3 = M00*X + M10*Y | M01X+M11Y
addpd xmm3, xmm2 ;xmm3 = M00*X + M10*Y+ M20 | M01*X + M11*Y + M20
add esi, 10h ;increment esi till next call of this function.
ret 0
TransformPoint ENDP
Key points to be mentioned:
Function is using SSE2/SSE3
instructions to calculate both coordinates.
Implementation of this function is
very essential to way how matrix elements are loaded.
In whole code, only this function
performs input data reading, that's why it increments esi
register (First memory access in algorithm). Result of this function
is stored in xmm3register and is used in future.
Function works properly only with
input data type of double and size of 8 bytes.
movupd instruction is used for data loading from
memory because it is not guaranteed that data are aligned to 16
bytes. For .Net C++ project I have found this build option, but for
C# projects, I did not.
Next functions FilterPoint and FilterPointDiscont
performs range points filtering. Difference is only that FilterPoint
function resets discontinuity flag and FilterPointDiscont
function sets this flag. Reason why it is done this way is that
through algorithm logic it is clear when discontinuity is necessary
and when not, so to avoid unnecessary checks and reduce execution
time almost same functionality was separated in two functions.

On the picture above blue and red squares represents result points
to be outputted. As you can see per one result point there are couple
of original points, so it is necessary to properly handle situations
when discontinuity marker is necessary and when not. Most interesting
is the topmost row, because discontinuity marker is not required even
curve goes out of drawing area in one case (top-left square) , but
required for another case (red square). So result will contains two
separate curves to be drawn. Let's see how it is handled:
;------------------------------------------------------------------------
;Function performs points simplification by range. If rounded to int point
;is same as previous, point is ignored. Point is outputted to ptr [edi]
;and increments edi register till next use.
;Function increments the counter of outputted points.
;Input:
;Point to examine located in xmm4 register
;Function uses MMX registers mm1, and mm0 to perform rounding and to store
;previously added point values.
;Function set discontinuity flag.
;------------------------------------------------------------------------
FilterPointDiscont PROC PRIVATE
shufpd xmm4,xmm4,1h ;xmm4= Xt,Yt
CVTPD2PI mm1,xmm4
cmp dword ptr[esp+4h], 0h ;check for first point
je __Add
;if not first point perform filtering
movq mm2,mm0
pcmpeqd mm2,mm1 ;if equal all bits of mm2 = 1b
movq mm3,mm2
PSRLQ mm3,20h
pand mm2,mm3
;if both coordinates are equal value will be FFFFFFFF,
;if one of them are not equal value will be 0
movd eax,mm2
cmp eax,0h
jne __Skip
__Add:
call OutputPoint
__Skip:
mov ebx, 01b
ret 0
FilterPointDiscont ENDP
;--------------------------------------------------------------------
;Function outputs result points.
;Input : mm1 contains point to be outputted.
ebx contains discontinuity flag 1 set discontinuity marker 0 do not set
edi register points to output buffer
[esp+8] counter of outputted points
;--------------------------------------------------------------------
OutputPoint PROC PRIVATE
test ebx,01b
jz AddPoint
movq [edi],mm7
add edi,8h
inc dword ptr[esp+8h]
AddPoint:
movq [edi],mm1
add edi,8h
movq mm0,mm1
inc dword ptr[esp+8h]
ret 0
OutputPoint ENDP
Points to be mentioned:
Function FilterPoint
resets discontinuity flag, and listed above FilterPointDiscont
sets discontinuity flag after points filtering are done, value of
this flag will affect next point output.
Function OutputPoint checks ebx
register used as discontinuity flag, and if flag is 1, outputs
discontinuity marker before current point output.
And finally there is code of top function implementing algorithm.
;---------------------------------------------------------------------
;Main Function to perform transfromations
;Features: Performs in one loop Affine transformation, curve clipping,
;and drawing points simplification
;Iteraction with used functions is performed throght registers.
;Parameters:
; _values -pointer to arrray of double values to be transformed, assume that values are located in maner
; x0,y0,x1,y1,...,xn-1,yn-1,xn,yn
; _count - unsigned integer values of points in _values array (!) count of Points= count of pairs X,Y
; but not the count of elements in _values array.
;_res - pointer to array of integers used as output buffer.
;_m00~_m21 - double numbers, representing elements of transformation matrix.
; Number - index of element(row,column)
;_xMin,xMax,yMin,yMax - double numbers representing clipping area.
;returns - count of points(!) after transformation.
;Notes:
;Because of curve clipping there possible cases then curve goes out of clipping area
;and than comes back and so on. To handle this cases,
;points of discontinuity are marked as 80000000h -32bit integer min value.
;----------------------------------------------------------------------
TransfromClipReducePoints PROC PUBLIC _values :DWORD,
_count :DWORD,
_res :DWORD,
_m00 :QWORD,
_m01 :QWORD,
_m10 :QWORD,
_m11 :QWORD,
_m20 :QWORD,
_m21 :QWORD,
_xMin :QWORD,
_yMin :QWORD,
_xMax :QWORD,
_yMax :QWORD
push ebx
push esi
push edi
;load parameters to corrensponding registers
mov esi, dword ptr[_values] ;input data
mov ecx, dword ptr[_count] ;input points count
mov edi, dword ptr[_res] ;destination pointer
;load transformation matrix to xmm0-xmm2 registers in a way:
; register Low | High
;-------------------------
; xmm0 m00 | m10
; xmm1 m01 | m11
; xmm2 m20 | m21
movsd xmm0,_m00
movhpd xmm0,_m10
movsd xmm1, _m01
movhpd xmm1, _m11
movsd xmm2, _m20
movhpd xmm2, _m21
;loading clipping bounds to xmm6, xmm7 registers in a way
; register Low | High
;-------------------------
; xmm6 xMin | yMin
; xmm7 xMax | yMax
movsd xmm6, _xMin
movhpd xmm6, _yMin
movsd xmm7, _xMax
movhpd xmm7, _yMax
;discontinuity marker loading to mm7 register
mov eax, 80000000h
push eax
push eax
movq mm7, [esp]
add esp,8h
xor eax, eax
push eax ;stack allocation for ouput points count.
xor ebx, ebx ;initialization to store discontinuity flag.
call TransformPoint
;calculating clipping bit code for calculated point and return value in [al] register.
call CalculateBitCode
;in this function during calculations xmm3 contains current point, and xmm5 previos point.
;Store calculated values as previous point
movapd xmm5, xmm3
;registers dl,dh are used to store clip bit codes
; dh - for point located in xmm5 (previos point)
; dl - for point located in xmm3 (current point)
mov dh,al
dec ecx ;because firs point is already processed
StartMainLoop:
call TransformPoint
call CalculateBitCode
mov dl,al ;dl - set dl to current point clip code
;Clipping. Check for two trivial cases
;1st trivial case: both points are outside and almoust on same side
;(same bit is on for both points)
test dl,dh ;test operation performs bitwise AND operation,
;so if same bit in both operators is set result will be not 0(zero)
jnz Continue
;put previous point to xmm4, as is Y,X
movapd xmm4,xmm5 ;because AddPoint use as input xmm4
;2nd trivial case, both points are inside the clipping area
mov al,dh
or al,dl
jnz ClipPrevPoint
;mov al,0h
call FilterPoint
jmp Continue
ClipPrevPoint:
cmp dh,0h
jnz ClipPrev
;mov al,0h
call FilterPoint
jmp ClipCurrentPoint
ClipPrev:
mov al,dh
call CalcClip ;uses eax, xmm3,xmm5 result stored in xmm4
;mov al,0h
call FilterPoint
ClipCurrentPoint:
movapd xmm4,xmm3
cmp dl,0h
jz Continue
mov al,dl
call CalcClip
;mov al,1h
call FilterPointDiscont
Continue:
movapd xmm5,xmm3 ;Store current point to previous
mov dh,dl ;Store current point clip code to previous
loop StartMainLoop
pop eax ;pop return value
emms ;clear MMX state.
pop edi
pop esi
pop ebx
ret 5ch
TransfromClipReducePoints ENDP
As you can see implementation is quite linear, and as you can test code provided performs required operations with really
super sonic speed. But of course, everything can not be so sweet. The
code provided have some restrictions:
- For correct work it is necessary
to implement class representing point in 2D. As provided
PointD
class. Important is that it is assumed that class contains only 2
member variables type of double. And order of variables is X,Y.
- Because even in sample code
PointD
class is a managed class, it is necessary to provide functionality
to get effective address of instance.
- For your needs you can inherit provided class
PointD
to extend its functionality, or create your own class, but do not
add member variables,because it will cause instance size change,as
result data corruption.
Using the Code
Even main code is done in assembler language, functionality is
easy accessible from managed code. And can be also used not only by
Windows Forms applications but also by ASP. Net applications to. Code
below demonstrates the implementation of
Tranformer::TransformDblToInt function. Of course you
can create your own but you need to follow next requirements for
correct work:
- Unmanaged code receive as input
array type of double, and it is assumed that values in array
represents 2d points coordinates like: x0,y0,x1,y1 and so on.
- It is necessary to provide enough
size output buffer.
- Result of unmanaged code is array
of
int and values are stored like, x0,y0,x1,y1 an so
on.
- Because of clipping and possible discontinuity, result
contains markers of discontinuity, values xi and yi are set to
int::MinValue (80000000h).
For more details please see source code.
List<array<Point>^>^ Transformer::TransformDblToInt(
array<PointD>^ dPoints,
double m00,
double m10,
double m20,
double m01,
double m11,
double m21,
double dXMin,
double dYMin,
double dXMax,
double dYMax)
{
if (piConvertBuffer->Length < dPoints->Length*4)
{
piConvertBuffer = gcnew array<int>(dPoints->Length*4);
}
pin_ptr<int> piRes = πConvertBuffer[0];
pin_ptr<double> piInput = dPoints[0].GetEffectiveAddress();
int iTotal= ::TransfromClipReducePoints(piInput,dPoints->Length, piRes,
m00,m01,m10,m11,m20,m21,dXMin,dYMin,dXMax,dYMax);
List<array<Point>^>^ oRes =gcnew List<array<Point>^>();
List<Point> oTemp = gcnew List<Point>();
for (int i=0;i< iTotal; i++)
{
if((int::MinValue == piConvertBuffer[i+i])&&(int::MinValue == piConvertBuffer[i+i+1]))
{
if ( 0 != oTemp.Count )
{
oRes->Add(oTemp.ToArray());
oTemp.Clear();
}
continue;
}
oTemp.Add(Point(piConvertBuffer[i+i],piConvertBuffer[i+i+1]));
}
if ( 0 != oTemp.Count )
{
oRes->Add(oTemp.ToArray());
oTemp.Clear();
}
oTemp.Clear();
if (0 == oRes->Count)
{
oRes = nullptr;
return nullptr;
}
return oRes;
}
Points of Interest
Main point of this article is to demonstrate that standard
libraries are still not perfect and that developers should always
think about optimization. Also i tried to show that if you want to
use full power of your CPU, even now only Assembly can help you.
Briefly next aspects are covered in code provided:
- Usage
SSE2/SSE3 and
MMX instructions.
- Interaction between managed and
unmanaged code
- Assembler files compilation using VS. Net (not inline
assembler, but pure *.asm files)
Notes
In demo program only time spend for pre-drawing processing is
counted. No drawing, no clipping and no points reduction performed
after transformation done by
System::Drawing::Drawing2d::Matrix::TransformPoints
method because it is not the matter of this article. Drawing
performed only for result of ::TransfromClipReducePoints
function.
Demo program generates y=cos(x) curve with random noise by y axis.
It is better to perform Douglas Pecker simplification algorithm on
result returned by ::TransfromClipReducePoints function,
but this is up to you. This algorithm was not used in my code because
this algorithm is not linear, and may get quite deep recursion if
curve points have a big noise.
Demo program does not perform CPUID check for SSE3 instructions
support, so please make sure that your CPU supports SSE3 instructions.
Simply your CPU must be P4 or above. For AMD CPUs - CPUs of same age as P4 do not
supports SSE3 instructions.
Resources used
History
Ver 1.0 from 28-Jul-2009
This member has not yet provided a Biography. Assume it's interesting and varied, and probably something to do with programming.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 









