Introduction
In this article, I want to explain and deduce the line drawing algorithm by Bresenham. Afterwards, I will show an optimized version which can be used to draw lines in Gecko based browsers like Mozilla or Firefox and Microsoft's Internet Explorer. As you know, HTML itself is not able to describe lines. Therefore, there is no built-in features in the above-mentioned browsers for drawing lines. By implementing the Bresenham algorithm with JavaScript while applying some tricks, we will be able to draw lines in a good manner in respect to the browser's runtime and memory footprints.
The Bresenham algorithm
The Bresenham algorithm aims at drawing an approximation of the mathematically correct line, which can be described in the form of a linear mathematical function. The demand for this algorithm came to hand when the first raster display or digital plotters were developed. These devices were unable to draw a continuous line in a strict mathematical sense. Rather, they were designed to plot a single pixel with a certain height and width on a screen coordinate. The approximation is based on finding the best and closest path on this raster display from the starting point to the end point.
The ideal line
The mathematical formula for describing a line is the following linear equation: y = m*x + b. In other words, a mathematical line is defined by a slope (variable m) and a pitch from the x-axis (variable b). By choosing two different points, we can, therefore, exactly define a line. To determine the two missing pieces of information (the slope and the pitch), we have to solve the following two equations:
I) y1 = m*x1 + b
II) y2 = m*x2 + b
=> I)
b = y1 - m*x1
=> II)
y2 = m*x2 + y1 - m*x1
y2 = m*(x2 - x1) + y1
m = (y2 - y1) / (x2 - x1) | x1 != x2
dy = y2 - y1
dx = x2 - x1
m = dy / dx
=> I)
b = y1 - (dy / dx) * x1
The following image illustrates the variables slope and pitch, and how they can be determined by two different points:

To draw a line from the starting point to the end point, we only have to loop from x1 to x2 and calculate the corresponding y-value. Our first approach for an algorithm to do this kind of drawing would look like the following:
function drawline1(x1, y1, x2, y2)
{
if (x1 == x2 && y1 == y2) {
setPixel(x1, y1);
return;
}
var dx = x2 - x1; var sx = (dx < 0) ? -1 : 1;
var dy = y2 - y1; var sy = (dy < 0) ? -1 : 1;
var m = dy / dx;
var b = y1 - m * x1;
while (x1 != x2)
{
var y = parseInt(Math.round(m*x1 + b));
setPixel(x1, y);
x1 += sx;
}
}
In the attached source files of this article, you will find a file called article_illustrations.html. Please open this file and refer to illustration A to test this algorithm directly. You have to choose two different points in the grid, and have to press the drawline button afterwards.
Imperfections of this algorithm
Drawing lines which slope reveals some of the imperfections of this algorithm. One major problem is that, in such a circumstance, the line becomes discontinuous in respect to the y-direction. An easy solution to this problem is to distinguish between those cases. When dy is greater than dx, the inner-loop of the algorithm must run stepwise in y-direction, otherwise vise versa in x-direction. This means that, we just change the x- and y-axis, or rotate the whole coordinate system by 90 degrees, making the new dy less than dx.
Making the algorithm work
When we apply this distinction, the algorithm will draw correct lines in respect to our wanted approximation.
function drawline2(x1, y1, x2, y2)
{
if (x1 == x2 && y1 == y2) {
setPixel(x1, y1);
return;
}
var dx = x2 - x1; var sx = (dx < 0) ? -1 : 1;
var dy = y2 - y1; var sy = (dy < 0) ? -1 : 1;
if (Math.abs(dy) < Math.abs(dx))
{
var m = dy / dx;
var b = y1 - m * x1;
while (x1 != x2)
{
setPixel(x1, parseInt(Math.round(m*x1 + b)));
x1 += sx;
}
}
else
{
var m = dx / dy;
var b = x1 - m * y1;
while (y1 != y2)
{
setPixel(parseInt(Math.round(m*y1 + b)), y1);
y1 += sy;
}
}
}
Please refer to illustration B within article_illustrations.html.
Optimizing the inner loops
The implemented algorithm, so far, draws lines quite well, but lacks on good performance. There are two reasons why the performance is pure. If you take a look at the operations which are performed in the inner loops of the algorithm, then you will recognize that the mathematical function, m*x + b is evaluated each time. Therefore, our first optimization efforts will be, to get rid of this evaluation, especially the multiplication. We do this by incrementally calculating the right y- or x-value. For the sake of simplicity, I will assume that dy is less than dx. Under this circumstance, we have to calculate the right y-value and the starting point will be y1. Because the slope of the line is less than or equal to one, we can only reduce or increase the y-position in each step of the inner loop maximally by one. But this is only done when the fraction becomes greater than one. Applying this trick to the algorithm allows us to leave the mathematical function beside. But due to the fact that the slope of the line has to be a floating value, these operations are still slow.
function drawline3(x1, y1, x2, y2)
{
if (x1 == x2 && y1 == y2) {
setPixel(x1, y1);
return;
}
var dx = x2 - x1; var sx = 1;
var dy = y2 - y1; var sy = 1;
if (dx < 0) {
sx = -1;
dx = -dx;
}
if (dy < 0) {
sy = -1;
dy = -dy;
}
if (dy < dx)
{
var m = dy / dx;
var fraction = 0.5 + m;
while (x1 != x2)
{
if (fraction > 1)
{
y1 += sy;
fraction -= 1;
}
fraction += m;
setPixel(x1, y1);
x1 += sx;
}
}
else
{
var m = dx / dy;
var fraction = 0.5 + m;
while (y1 != y2)
{
if (fraction > 1)
{
x1 += sx;
fraction -= 1;
}
fraction += m;
setPixel(x1, y1);
y1 += sy;
}
}
}
But we can prevent this, by multiplying the slope with 2*dx or 2*dy, accordingly. This prevents the slope from becoming less than one, which allows us to use integer values.
var fraction = dx + 2*dy;
while (x1 != x2)
{
if (fraction > 2*dx)
{
y1 += sy;
fraction -= 2*dx;
}
fraction += 2*dy;
this.setPixel(x1, y1);
x1 += sx;
}
If you look at the above code, there are some more optimizations left. First, there are a lot of places where 2*dx or 2*dy is used. Pre-calculating these values is a real performance burst. Finally, microcontrollers are faster when it comes to testing variables against zero. Therefore, the if statement will be modified to test against zero, and not 2*dx, which means, that we have to subtract 2*dx from the fraction. Frankly, I do not know if this optimization has any effect in a script language like JavaScript, but the original Bresenham algorithm proposes this, so I have mentioned this here.
The final Bresenham algorithm
function drawline4(x1, y1, x2, y2)
{
var dx = x2 - x1; var sx = 1;
var dy = y2 - y1; var sy = 1;
if (dx < 0) {
sx = -1;
dx = -dx;
}
if (dy < 0) {
sy = -1;
dy = -dy;
}
dx = dx << 1;
dy = dy << 1;
this.setPixel(x1, y1);
if (dy < dx)
{
var fraction = dy - (dx>>1);
while (x1 != x2)
{
if (fraction >= 0)
{
y1 += sy;
fraction -= dx;
}
fraction += dy;
x1 += sx;
setPixel(x1, y1);
}
}
else
{
var fraction = dx - (dy>>1);
while (y1 != y2)
{
if (fraction >= 0)
{
x1 += sx;
fraction -= dy;
}
fraction += dx;
y1 += sy;
setPixel(x1, y1);
}
}
}
See illustration C in article_illustrations.html.
Using the Bresenham algorithm to draw lines in browsers
Now, we have a quite optimized JavaScript version of the line drawing algorithm by Bresenham. In the inner loops of this algorithm, there are calls to an obscure setPixel function. Currently, this function sets a style attribute of the grid's corresponding cell element. Because this is not sufficient, we have to consider how we will print pixels in browsers. A straightforward solution is, to create a floating div element at the corresponding position whose height and width is exactly one pixel. As HTML is able to position elements absolutely, this is a possible way to draw pixels in the browser's drawing area. But you can imagine, that creating div elements for every pixel of a line is a very slow and exaggerated activity. Never mind, what kind of data structures the browser has to manage to create and show an element like this. Therefore, our implementation and adaptation of this line drawing algorithm will exactly create one div element for each step of the rasterized approximation. The illustration below shows what the adapted algorithm will do:
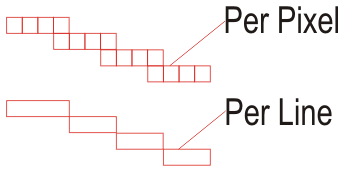
Instead of drawing each pixel of a line separately, it will union them appropriately in a line based manner, creating one div element for each of these combined lines. If you look at the illustration, this means, that instead of creating 16 elements, the algorithm will create only four different div tags, leading to nearly four times better runtime characteristics.
The code below adapts this idea to our line drawing algorithm. When the fraction is greater than zero, we have to change the corresponding x- or y-direction. At this point, the new algorithm draws a line, unifying all pixels in a row or column. Using this technique, we have amazing speed and memory benefits, especially when it come to long lines, the benefits are more than what I told you in the above illustration.
function drawline5(x1, y1, x2, y2)
{
if (x1 > x2) {
var tmpx = x1; var tmpy = y1;
x1 = x2; y1 = y2;
x2 = tmpx; y2 = tmpy;
}
var dx = x2 - x1;
var dy = y2 - y1; var sy = 1;
if (dy < 0) {
sy = -1;
dy = -dy;
}
dx = dx << 1; dy = dy << 1;
if (dy <= dx)
{
var fraction = dy - (dx>>1);
var mx = x1;
while (x1 != x2)
{
x1++;
if (fraction >= 0)
{
setPixel2(mx, y1,x1-mx,1);
y1 += sy;
mx = x1;
fraction -= dx;
}
fraction += dy;
}
setPixel2(mx,y1,x1-mx,1);
}
else
{
var fraction = dx - (dy>>1);
var my = y1;
if (sy > 0)
{
while (y1 != y2)
{
y1++;
if (fraction >= 0)
{
setPixel2(x1++, my,1,y1-my);
my = y1;
fraction -= dy;
}
fraction += dx;
}
setPixel2(x1,my,1,y1-my);
}
else
{
while (y1 != y2)
{
y1--;
if (fraction >= 0)
{
setPixel2(x1++, y1,1,my-y1);
my = y1;
fraction -= dy;
}
fraction += dx;
}
setPixel2(x1,y1,1,my-y1);
}
}
}
How to use the drawline function
There are two ways of using this code in your web pages which is provided and encapsulated by a JavaScript class called Graphics. The first way is, to directly draw into the document when the page is being loaded and processed. You can achieve this, by placing the following code somewhere within the body element. This code writes JavaScript statements for creating each div element in the document. When the page is loaded, your lines are visible immediately. In this case, the coordinate system of the graphics context which is responsible for drawing the lines starts from the upper left corner of the browser's visible drawing area.
var g = new Graphics();
g.drawLine(100,50,200,70);
g.paint();
The other way to use this code is by drawing the lines after the page has been loaded. In this mode, the lines are drawn and connected with a container. Normally, this container can be another div element. To create a graphics context and connect it with a container, you have to set the id of the container while you create the context. The coordinate system, in this case, starts from the upper left corner of the container. The following code is needed to achieve the functionality:
var linecanvas_graphics = new Graphics('linecanvas');
function drawCanvas()
{
try {
var x1 = parseInt(document.getElementById('in_x1').value);
var y1 = parseInt(document.getElementById('in_y1').value);
var x2 = parseInt(document.getElementById('in_x2').value);
var y2 = parseInt(document.getElementById('in_y2').value);
var start = (new Date()).getTime();
linecanvas_graphics.drawLine(x1, y1, x2, y2);
linecanvas_graphics.paint();
var stop = (new Date()).getTime();
alert("This operation took " + (stop-start) + "ms");
} catch(e) {
alert("an error has occured, when the input values were parsed" + e);
}
}
Conclusions and future work
I had the idea for this code when I saw Julijan Sribar's article about a 3D charting control, which can be found here. Some years ago, I had to code such a control in a server-side version, where only the graphics was drawn and send to the client's browser. As you can imagine, this approach does not provide much functionality on the client. Therefore, I thought of drawing this charting graphic on the client, but the lack of drawing capabilities of modern browsers frustrated me. I now have started working on a JavaScript based drawing library, which is capable of drawing most of the same elements the Windows API provides. This line drawing code is an extract of the code. I hope to finish this library someday and post it here. (Hey, where else, right? ;) For now, this line drawing code works quite well on Mozilla based browsers and the Internet Explorer. Actually, I have some problems with the IE, because it creates the div elements much slower than Mozilla, and I don't have a clue, why this happens. Another thing is that, IE does not draw the lines as clean and well as Mozilla. I hope to fix that in future. Please, try this code out and give me some feedback.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 








 ;y1
;y1
