Introduction
Math problems have a charm of their own. Besides, they help to develop a programmer's skill. Here, we describe a student's exam task: "Develop an application that models the behaviour of a Hypocycloid".
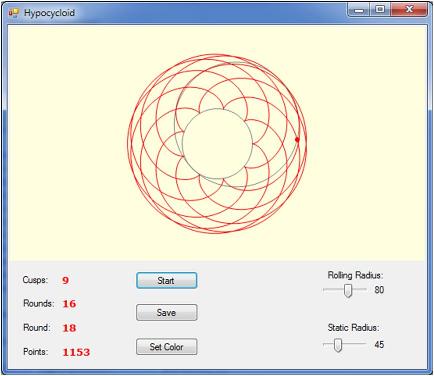
Background
A cycloid is the curve defined by the path of a point on the edge of a circular wheel as the wheel rolls along a straight line. It was named by Galileo in 1599 (http://en.wikipedia.org/wiki/Cycloid).
A hypocycloid is a curve generated by the trace of a fixed point on a small circle that rolls within a larger circle. It is comparable to the cycloid, but instead of the circle rolling along a line, it rolls within a circle.
Use Google to find a wonderful book of Eli Maor, Trigonometric Delights (Princeton, New Jersey). The following passage is taken from this book.
I believe that a program developer must love formulas derivation. Hence, let us find the parametric equations of the hypocycloid.

A point on a circle of radius r rolls on the inside of a fixed circle of radius R. Let C be the center of the rolling circle, and P a point on the moving circle. When the rolling circle turns through an angle in a clockwise direction, C traces an arc of angular width t in a counterclockwise direction. Assuming that the motion starts when P is in contact with the fixed circle (figure on the left), we choose a coordinate system in which the origin is at O and the x-axis points to P. The coordinates of P relative to C are:
(r cos b; -r sin b)
The minus sign in the second coordinate is there because b is measured clockwise. Coordinates of C relative to O are:
((R - r) cos t, (R - r) sin t)
Note, angle b may be expressed as:
b = t + β; β = b - t
Thus, the coordinates of P relative to O are:
((R - r) cos t + r cos β, (R - r) sin t - r sin β) (1)
But the angles t and b are not independent: as the motion progresses, the arcs of the fixed and moving circles that come in contact must be of equal length L.
L = R t L = r b
Using this relation to express b in terms of t, we get
b = R t / r
Equations (1) become:
x = (R - r) cos t + r cos ((R / r - 1) t) (2)
y = (R - r) sin t - r sin ((R / r - 1) t)
Equations (2) are the parametric equations of the hypocycloid, the angle t being the parameter (if the rolling circle rotates with constant angular velocity, t will be proportional to the elapsed time since the motion began). The general shape of the curve depends on the ratio R/r. If this ratio is a fraction m/n in lowest terms, the curve will have m cusps (corners), and it will be completely traced after moving the wheel n times around the inner rim. If R/r is irrational, the curve will never close, although going around the rim many times will nearly close it.
Using the code
The demo application provided with this article uses a Hypocycloid control derived from UserControl to model a behaviour of a hypocycloid described above.
The functionality of the hypocycloid is implemented in the Hypocycloid class. It has a GraphicsPath path data field that helps to render the hypocycloid path over time. A floating point variable, angle, corresponds to the angle t described earlier.
- Variable
ratio = R / r delta = R - r
All the math is done within the timer Tick event handler.
void timer_Tick(object sender, EventArgs e)
{
angle += step;
double
cosa = Math.Cos(angle),
sina = Math.Sin(angle),
ct = ratio * angle;
movingCenter.X = (float)(centerX + delta * cosa);
movingCenter.Y = (float)(centerY + delta * sina);
PointF old = point;
point = new PointF(
movingCenter.X + r * (float)Math.Cos(ct),
movingCenter.Y - r * (float)Math.Sin(ct));
int n = (int)(angle / pi2);
if (n > round)
{
round = n;
ParentNotify(msg + ";" + round);
}
if (round < nRounds)
path.AddLine(old, point);
else if (!stopPath)
{
ParentNotify(msg + ";" + round + ";" + path.PointCount);
stopPath = true;
}
parent.Invalidate();
}
ParentNotify is the event of the generic delegate type Action<string>.
public event Action<string> ParentNotify;
We use it to notify a parent control of a current angle (round).
Besides a constructor, the class has the following public methods: Reset, Draw, Start, Stop, and SaveToFile. Remember also that the Y axis in a Windows window goes down.
Peter the Great St. Petersburg Polytechnic University professor,
Microsoft Authorized Educational Center trainer,
Microsoft Certified Professional (C# Desktop Apps and MFC)
Lectures on OOP, C# and C++, Windows programming with C# and C++.
Have long practice and experience in finding the right way to formulate and numerically solve differential equations.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 










 BTW: I would not explicitly called using of OFD instead SFD a mistake ... it just point of view... It would be worse mistake to use SFD instead OFD, by my opinion
BTW: I would not explicitly called using of OFD instead SFD a mistake ... it just point of view... It would be worse mistake to use SFD instead OFD, by my opinion 