Neural Network for Recognition of Handwritten Digits
4.97/5 (235 votes)
Dec 5, 2006
68 min read
2859260
57577
A convolutional neural network achieves 99.26% accuracy on a modified NIST database of hand-written digits.
- Download the Neural Network demo project - 203 Kb (includes a release-build executable that you can run without the need to compile)
- Download a sample neuron weight file - 2,785 Kb (achieves the 99.26% accuracy mentioned above)
- Download the MNIST database - 11,594 Kb total for all four files (external link to four files which are all required for this project)
Contents
- Introduction
- Some Neural Network Theory
- Structure of the Convolutional Neural Network
- MNIST Database of Handwritten Digits
- Overall Architecture of the Test/Demo Program
- Training the Neural Network
- Tricks That Make Training Faster
- Experiences in Training the Neural Network
- Results
- Bibliography
- License and Version Information
Introduction
This article chronicles the development of an artificial neural network designed to recognize handwritten digits. Although some theory of neural networks is given here, it would be better if you already understood some neural network concepts, like neurons, layers, weights, and backpropagation.
The neural network described here is not a general-purpose neural network, and it's not some kind of a neural network workbench. Rather, we will focus on one very specific neural network (a five-layer convolutional neural network) built for one very specific purpose (to recognize handwritten digits).
The idea of using neural networks for the purpose of recognizing handwritten digits is not a new one. The inspiration for the architecture described here comes from articles written by two separate authors. The first is Dr. Yann LeCun, who was an independent discoverer of the basic backpropagation algorithm. Dr. LeCun hosts an excellent site on his research into neural networks. In particular, you should view his "Learning and Visual Perception" section, which uses animated GIFs to show results of his research. The MNIST database (which provides the database of handwritten digits) was developed by him. I used two of his publications as primary source materials for much of my work, and I highly recommend reading his other publications too (they're posted at his site). Unlike many other publications on neural networks, Dr. LeCun's publications are not inordinately theoretical and math-intensive; rather, they are extremely readable, and provide practical insights and explanations. His articles and publications can be found here. Here are the two publications that I relied on:
- Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner, "Gradient-Based Learning Applied to Document Recognition," Proceedings of the IEEE, vol. 86, no. 11, pp. 2278-2324, Nov. 1998. [46 pages]
- Y. LeCun, L. Bottou, G. Orr, and K. Muller, "Efficient BackProp," in Neural Networks: Tricks of the trade, (G. Orr and Muller K., eds.), 1998. [44 pages]
The second author is Dr. Patrice Simard, a former collaborator with Dr. LeCun when they both worked at AT&T Laboratories. Dr. Simard is now a researcher at Microsoft's "Document Processing and Understanding" group. His articles and publications can be found here, and the publication that I relied on is:
- Patrice Y. Simard, Dave Steinkraus, John Platt, "Best Practices for Convolutional Neural Networks Applied to Visual Document Analysis,"
 International Conference on Document Analysis and Recognition (ICDAR), IEEE Computer Society, Los Alamitos, pp. 958-962, 2003.
International Conference on Document Analysis and Recognition (ICDAR), IEEE Computer Society, Los Alamitos, pp. 958-962, 2003.
One of my goals here was to reproduce the accuracy achieved by Dr. LeCun, who was able to train his neural network to achieve 99.18% accuracy (i.e., an error rate of only 0.82%). This error rate served as a type of "benchmark", guiding my work.
As a final introductory note, I'm not overly proud of the source code, which is most definitely an engineering work-in-progress. I started out with good intentions, to make source code that was flexible and easy to understand and to change. As things progressed, the code started to turn ugly. I began to write code simply to get the job done, sometimes at the expense of clean code and comprehensibility. To add to the mix, I was also experimenting with different ideas, some of which worked and some of which did not. As I removed the failed ideas, I did not always back out all the changes and there are therefore some dangling stubs and dead ends. I contemplated the possibility of not releasing the code. But that was one of my criticisms of the articles I read: none of them included code. So, with trepidation and the recognition that the code is easy to criticize and could really use a re-write, here it is.
Some Neural Network Theory
This is not a neural network tutorial, but to understand the code and the names of the variables used in it, it helps to see some neural networks basics.
The following discussion is not completely general. It considers only feed-forward neural networks, that is, neural networks composed of multiple layers, in which each layer of neurons feeds only the very next layer of neurons, and receives input only from the immediately preceding layer of neurons. In other words, the neurons don't skip layers.
Consider a neural network that is composed of multiple layers, with multiple neurons in each layer. Focus on one neuron in layer n, namely the i-th neuron. This neuron gets its inputs from the outputs of neurons in the previous layer, plus a bias whose valued is one ("1"). I use the variable "x" to refer to outputs of neurons. The i-th neuron applies a weight to each of its inputs, and then adds the weighted inputs together so as to obtain something called the "activation value". I use the variable "y" to refer to activation values. The i-th neuron then calculates its output value "x" by applying an "activation function" to the activation value. I use the letter "F()" to refer to the activation function. The activation function is sometimes referred to as a "Sigmoid" function, a "Squashing" function and other names, since its primary purpose is to limit the output of the neuron to some reasonable range like a range of -1 to +1, and thereby inject some degree of non-linearity into the network. Here's a diagram of a small part of the neural network; remember to focus on the i-th neuron in level n:

This is what each variable means:
|
|
is the output of the i-th neuron in layer n |
|
|
is the output of the j-th neuron in layer n-1 |
|
|
is the output of the k-th neuron in layer n-1 |
|
|
is the weight that the i-th neuron in layer n applies to the output of the j-th neuron from layer n-1 (i.e., the previous layer). In other words, it's the weight from the output of the j-th neuron in the previous layer to the i-th neuron in the current (n-th) layer. |
|
|
is the weight that the i-th neuron in layer n applies to the output of the k-th neuron in layer n-1 |
|
|
is the general feed-forward equation, where F() is the activation function. We will discuss the activation function in more detail in a moment. |
How does this translate into code and C++ classes? The way I saw it, the above diagram suggested that a neural network is composed of objects of four different classes: layers, neurons in the layers, connections from neurons in one layer to those in another layer, and weights that are applied to connections. Those four classes are reflected in the code, together with a fifth class -- the neural network itself -- which acts as a container for all other objects and which serves as the main interface with the outside world. Here's a simplified view of the classes. Note that the code makes heavy use of std::vector, particularly std::vector< double >:
// simplified view: some members have been omitted, // and some signatures have been altered // helpful typedef's typedef std::vector< NNLayer* > VectorLayers; typedef std::vector< NNWeight* > VectorWeights; typedef std::vector< NNNeuron* > VectorNeurons; typedef std::vector< NNConnection > VectorConnections; // Neural Network class class NeuralNetwork { public: NeuralNetwork(); virtual ~NeuralNetwork(); void Calculate( double* inputVector, UINT iCount, double* outputVector = NULL, UINT oCount = 0 ); void Backpropagate( double *actualOutput, double *desiredOutput, UINT count ); VectorLayers m_Layers; }; // Layer class class NNLayer { public: NNLayer( LPCTSTR str, NNLayer* pPrev = NULL ); virtual ~NNLayer(); void Calculate(); void Backpropagate( std::vector< double >& dErr_wrt_dXn /* in */, std::vector< double >& dErr_wrt_dXnm1 /* out */, double etaLearningRate ); NNLayer* m_pPrevLayer; VectorNeurons m_Neurons; VectorWeights m_Weights; }; // Neuron class class NNNeuron { public: NNNeuron( LPCTSTR str ); virtual ~NNNeuron(); void AddConnection( UINT iNeuron, UINT iWeight ); void AddConnection( NNConnection const & conn ); double output; VectorConnections m_Connections; }; // Connection class class NNConnection { public: NNConnection(UINT neuron = ULONG_MAX, UINT weight = ULONG_MAX); virtual ~NNConnection(); UINT NeuronIndex; UINT WeightIndex; }; // Weight class class NNWeight { public: NNWeight( LPCTSTR str, double val = 0.0 ); virtual ~NNWeight(); double value; };
As you can see from the above, class NeuralNetwork stores a vector of pointers to layers in the neural network, which are represented by class NNLayer. There is no special function to add a layer (there probably should be one); simply use the std::vector::push_back() function. The NeuralNetwork class also provides the two primary interfaces with the outside world, namely, a function to forward propagate the neural network (the Calculate() function) and a function to Backpropagate() the neural network so as to train it.
Each NNLayer stores a pointer to the previous layer, so that it knows where to look for its input values. In addition, it stores a vector of pointers to the neurons in the layer, represented by class NNNeuron, and a vector of pointers to weights, represented by class NNWeight. Similar to the NeuralNetwork class, the pointers to the neurons and to the weights are added using the std::vector::push_back() function. Finally, the NNLayer class includes functions to Calculate() the output values of neurons in the layer, and to Backpropagate() them; in fact, the corresponding function in the NeuralNetwork class simply iterate through all layers in the network and call these functions.
Each NNNeuron stores a vector of connections that tell the neurons where to get its inputs. Connections are added using the NNNeuron::AddConnection() function, which takes an index to a neuron and an index to a weight, constructs a NNConnection object, and push_back()'s the new connection onto the vector of connections. Each neuron also stores its own output value, even though it's the NNLayer class that is responsible for calculating the actual value of the output and storing it there. The NNConnection and NNWeight classes respectively store obviously-labeled information.
One legitimate question about the class structure is, why are there separate classes for the weights and the connections? According to the diagram above, each connection has a weight, so why not put them in the same class? The answer lies in the fact that weights are often shared between connections. In fact, the convolutional neural network of this program specifically shares weights amongst its connections. So, for example, even though there might be several hundred neurons in a layer, there might only be a few dozen weights due to sharing. By making the NNWeight class separate from the NNConnection class, this sharing is more readily accomplished.
Forward Propagation
Forward propagation is the process whereby each of all of the neurons calculates its output value, based on inputs provided by the output values of the neurons that feed it.
In the code, the process is initiated by calling NeuralNetwork::Calculate(). NeuralNetwork::Calculate() directly sets the values of neurons in the input layer, and then iterates through the remaining layers, calling each layer's NNLayer::Calculate() function. This results in a forward propagation that's completely sequential, starting from neurons in the input layer and progressing through to the neurons in the output layer. A sequential calculation is not the only way to forward propagate, but it's the most straightforward. Here's simplified code, which takes a pointer to a C-style array of doubles representing the input to the neural network, and stores the output of the neural network to another C-style array of doubles:
// simplified code void NeuralNetwork::Calculate(double* inputVector, UINT iCount, double* outputVector /* =NULL */, UINT oCount /* =0 */) { VectorLayers::iterator lit = m_Layers.begin(); VectorNeurons::iterator nit; // first layer is input layer: directly // set outputs of all of its neurons // to the given input vector if ( lit < m_Layers.end() ) { nit = (*lit)->m_Neurons.begin(); int count = 0; ASSERT( iCount == (*lit)->m_Neurons.size() ); // there should be exactly one neuron per input while( ( nit < (*lit)->m_Neurons.end() ) && ( count < iCount ) ) { (*nit)->output = inputVector[ count ]; nit++; count++; } } // iterate through remaining layers, // calling their Calculate() functions for( lit++; lit<m_Layers.end(); lit++ ) { (*lit)->Calculate(); } // load up output vector with results if ( outputVector != NULL ) { lit = m_Layers.end(); lit--; nit = (*lit)->m_Neurons.begin(); for ( int ii=0; ii<oCount; ++ii ) { outputVector[ ii ] = (*nit)->output; nit++; } } }
Inside the layer's Calculate() function, the layer iterates through all neurons in the layer, and for each neuron the output is calculated according to the feed-forward formula given above, namely

This formula is applied by iterating through all connections for the neuron, and for each connection, obtaining the corresponding weight and the corresponding output value from a neuron in the previous layer:
// simplified code void NNLayer::Calculate() { ASSERT( m_pPrevLayer != NULL ); VectorNeurons::iterator nit; VectorConnections::iterator cit; double dSum; for( nit=m_Neurons.begin(); nit<m_Neurons.end(); nit++ ) { NNNeuron& n = *(*nit); // to ease the terminology cit = n.m_Connections.begin(); ASSERT( (*cit).WeightIndex < m_Weights.size() ); // weight of the first connection is the bias; // its neuron-index is ignored dSum = m_Weights[ (*cit).WeightIndex ]->value; for ( cit++ ; cit<n.m_Connections.end(); cit++ ) { ASSERT( (*cit).WeightIndex < m_Weights.size() ); ASSERT( (*cit).NeuronIndex < m_pPrevLayer->m_Neurons.size() ); dSum += ( m_Weights[ (*cit).WeightIndex ]->value ) * ( m_pPrevLayer->m_Neurons[ (*cit).NeuronIndex ]->output ); } n.output = SIGMOID( dSum ); } }
In this code, SIGMOID is #defined to the activation function, which is described in the next section.
The Activation Function (or, "Sigmoid" or "Squashing" Function)
Selection of a good activation function is an important part of the design of a neural network. Generally speaking, the activation function should be symmetric, and the neural network should be trained to a value that is lower than the limits of the function.
One function that should never be used as the activation function is the classical sigmoid function (or "logistic" function), defined as ![]() . It should never be used since it is not symmetric: its value approaches +1 for increasing x, but for decreasing x its value approaches zero (i.e., it does not approach -1 which it should for symmetry). The reason the logistic function is even mentioned here is that there are many articles on the web that recommend its use in neural networks, for example, Sigmoid function in the Wikipedia. In my view, this is a poor recommendation and should be avoided.
. It should never be used since it is not symmetric: its value approaches +1 for increasing x, but for decreasing x its value approaches zero (i.e., it does not approach -1 which it should for symmetry). The reason the logistic function is even mentioned here is that there are many articles on the web that recommend its use in neural networks, for example, Sigmoid function in the Wikipedia. In my view, this is a poor recommendation and should be avoided.
One good selection for the activation function is the hyperbolic tangent, or ![]() . This function is a good choice because it's completely symmetric, as shown in the following graph. If used, then do not train the neural network to ±1.0. Instead, choose an intermediate value, like ±0.8.
. This function is a good choice because it's completely symmetric, as shown in the following graph. If used, then do not train the neural network to ±1.0. Instead, choose an intermediate value, like ±0.8.

Another reason why hyperbolic tangent is a good choice is that it's easy to obtain its derivative. Yes, sorry, but a bit of calculus is needed in neural networks. Not only is it easy to obtain its derivative, but also the value of derivative can be expressed in terms of the output value (i.e., as opposed to the input value). More specifically, given that:
 , where (using the notation established above) y is the input to the function (corresponding to the activation value of a neuron) and x is the output of the neuron.
, where (using the notation established above) y is the input to the function (corresponding to the activation value of a neuron) and x is the output of the neuron.
Then 
Which simplifies to ![]()
Or, since ![]() , the result is
, the result is ![]() . This result means that we can calculate the value of the derivative of F() given only the output of the function, without any knowledge of the input. In this article, we will refer to the derivative of the activation function as G(x).
. This result means that we can calculate the value of the derivative of F() given only the output of the function, without any knowledge of the input. In this article, we will refer to the derivative of the activation function as G(x).
The activation function used in the code is a scaled version of the hyperbolic tangent. It was chosen based on a recommendation in one of Dr. LeCun's articles. Scaling causes the function to vary between ±1.7159, and permits us to train the network to values of ±1.0.
Backpropagation
Backpropagation is an iterative process that starts with the last layer and moves backwards through the layers until the first layer is reached. Assume that for each layer, we know the error in the output of the layer. If we know the error of the output, then it is not hard to calculate changes for the weights, so as to reduce that error. The problem is that we can only observe the error in the output of the very last layer.
Backpropagation gives us a way to determine the error in the output of a prior layer given the output of a current layer. The process is therefore iterative: start at the last layer and calculate the change in the weights for the last layer. Then calculate the error in the output of the prior layer. Repeat.
The backpropagation equations are given below. My purpose in showing you the equations is so that you can find them in the code, and understand them. For example, the first equation shows how to calculate the partial derivative of the error EP with respect to the activation value yi at the n-th layer. In the code, you will see a variable named dErr_wrt_dYn[ ii ].
Start the process off by computing the partial derivative of the error due to a single input image pattern with respect to the outputs of the neurons on the last layer. The error due to a single pattern is calculated as follows:
|
|
(equation 1) |
where:
|
|
is the error due to a single pattern P at the last layer n; |
|
|
is the target output at the last layer (i.e., the desired output at the last layer); and |
|
|
is the actual value of the output at the last layer. |
Given equation (1), then taking the partial derivative yields:
|
|
(equation 2) |
Equation (2) gives us a starting value for the backpropagation process. We use the numeric values for the quantities on the right side of equation (2) in order to calculate numeric values for the derivative. Using the numeric values of the derivative, we calculate the numeric values for the changes in the weights, by applying the following two equations (3) and then (4):
|
|
(equation 3) |
| where |
|
is the derivative of the activation function. |
 |
(equation 4) |
Then, using equation (2) again and also equation (3), we calculate the error for the previous layer, using the following equation (5):
|
|
(equation 5) |
The values we obtain from equation (5) are used as starting values for the calculations on the immediately preceding layer. This is the single most important point in understanding backpropagation. In other words, we take the numeric values obtained from equation (5), and use them in a repetition of equations (3), (4) and (5) for the immediately preceding layer.
Meanwhile, the values from equation (4) tell us how much to change the weights in the current layer n, which was the whole purpose of this gigantic exercise. In particular, we update the value of each weight according to the formula:
|
|
(equation 6) |
where eta is the "learning rate", typically a small number like 0.0005 that is gradually decreased during training.
In the code, these equations are implemented by calling NeuralNetwork::Backpropagate(). The input to the NeuralNetwork::Backpropagate() function is the actual output of the neural network and the desired output. Using these two inputs, the NeuralNetwork::Backpropagate() function calculates the value of equation (2). It then iterates through all layers in the network, starting from the last layer and proceeding backwards toward the first layer. For each layer, the layer's NNLayer::Backpropagate() function is called. The input to NNLayer::Backpropagate() is the derivative, and the output is equation (5). These derivatives are all stored in a vector of a vector of doubles named differentials. The output from one layer is then fed as the input to the next preceding layer:
// simplified code void NeuralNetwork::Backpropagate(double *actualOutput, double *desiredOutput, UINT count) { // Backpropagates through the neural net // Proceed from the last layer to the first, iteratively // We calculate the last layer separately, and first, // since it provides the needed derviative // (i.e., dErr_wrt_dXnm1) for the previous layers // nomenclature: // // Err is output error of the entire neural net // Xn is the output vector on the n-th layer // Xnm1 is the output vector of the previous layer // Wn is the vector of weights of the n-th layer // Yn is the activation value of the n-th layer, // i.e., the weighted sum of inputs BEFORE // the squashing function is applied // F is the squashing function: Xn = F(Yn) // F' is the derivative of the squashing function // Conveniently, for F = tanh, // then F'(Yn) = 1 - Xn^2, i.e., the derivative can be // calculated from the output, without knowledge of the input VectorLayers::iterator lit = m_Layers.end() - 1; std::vector< double > dErr_wrt_dXlast( (*lit)->m_Neurons.size() ); std::vector< std::vector< double > > differentials; int iSize = m_Layers.size(); differentials.resize( iSize ); int ii; // start the process by calculating dErr_wrt_dXn for the last layer. // for the standard MSE Err function // (i.e., 0.5*sumof( (actual-target)^2 ), this differential is simply // the difference between the target and the actual for ( ii=0; ii<(*lit)->m_Neurons.size(); ++ii ) { dErr_wrt_dXlast[ ii ] = actualOutput[ ii ] - desiredOutput[ ii ]; } // store Xlast and reserve memory for // the remaining vectors stored in differentials differentials[ iSize-1 ] = dErr_wrt_dXlast; // last one for ( ii=0; ii<iSize-1; ++ii ) { differentials[ ii ].resize( m_Layers[ii]->m_Neurons.size(), 0.0 ); } // now iterate through all layers including // the last but excluding the first, and ask each of // them to backpropagate error and adjust // their weights, and to return the differential // dErr_wrt_dXnm1 for use as the input value // of dErr_wrt_dXn for the next iterated layer ii = iSize - 1; for ( lit; lit>m_Layers.begin(); lit--) { (*lit)->Backpropagate( differentials[ ii ], differentials[ ii - 1 ], m_etaLearningRate ); --ii; } differentials.clear(); }
Inside the NNLayer::Backpropagate() function, the layer implements equations (3) through (5) in order to determine the derivative for use by the next preceding layer. It then implements equation (6) in order to update the weights in its layer. In the following code, the derivative of the activation function G(x) is #defined as DSIGMOID:
// simplified code void NNLayer::Backpropagate( std::vector< double >& dErr_wrt_dXn /* in */, std::vector< double >& dErr_wrt_dXnm1 /* out */, double etaLearningRate ) { double output; // calculate equation (3): dErr_wrt_dYn = F'(Yn) * dErr_wrt_Xn for ( ii=0; ii<m_Neurons.size(); ++ii ) { output = m_Neurons[ ii ]->output; dErr_wrt_dYn[ ii ] = DSIGMOID( output ) * dErr_wrt_dXn[ ii ]; } // calculate equation (4): dErr_wrt_Wn = Xnm1 * dErr_wrt_Yn // For each neuron in this layer, go through // the list of connections from the prior layer, and // update the differential for the corresponding weight ii = 0; for ( nit=m_Neurons.begin(); nit<m_Neurons.end(); nit++ ) { NNNeuron& n = *(*nit); // for simplifying the terminology for ( cit=n.m_Connections.begin(); cit<n.m_Connections.end(); cit++ ) { kk = (*cit).NeuronIndex; if ( kk == ULONG_MAX ) { output = 1.0; // this is the bias weight } else { output = m_pPrevLayer->m_Neurons[ kk ]->output; } dErr_wrt_dWn[ (*cit).WeightIndex ] += dErr_wrt_dYn[ ii ] * output; } ii++; } // calculate equation (5): dErr_wrt_Xnm1 = Wn * dErr_wrt_dYn, // which is needed as the input value of // dErr_wrt_Xn for backpropagation of the next (i.e., previous) layer // For each neuron in this layer ii = 0; for ( nit=m_Neurons.begin(); nit<m_Neurons.end(); nit++ ) { NNNeuron& n = *(*nit); // for simplifying the terminology for ( cit=n.m_Connections.begin(); cit<n.m_Connections.end(); cit++ ) { kk=(*cit).NeuronIndex; if ( kk != ULONG_MAX ) { // we exclude ULONG_MAX, which signifies // the phantom bias neuron with // constant output of "1", // since we cannot train the bias neuron nIndex = kk; dErr_wrt_dXnm1[ nIndex ] += dErr_wrt_dYn[ ii ] * m_Weights[ (*cit).WeightIndex ]->value; } } ii++; // ii tracks the neuron iterator } // calculate equation (6): update the weights // in this layer using dErr_wrt_dW (from // equation (4) and the learning rate eta for ( jj=0; jj<m_Weights.size(); ++jj ) { oldValue = m_Weights[ jj ]->value; newValue = oldValue.dd - etaLearningRate * dErr_wrt_dWn[ jj ]; m_Weights[ jj ]->value = newValue; } }
Second Order Methods
All second order techniques have one goal in mind: to increase the speed with which backpropagation converges to optimal weights. All second order techniques (at least in principle) accomplish this in the same fundamental way: by adjusting each weight differently, e.g., by applying a learning rate eta that differs for each individual weight.
In his "Efficient BackProp, article, Dr. LeCun proposes a second order technique that he calls the "stochastic diagonal Levenberg-Marquardt method". He compares the performance of this method with a "carefully tuned stochastic gradient algorithm", which is an algorithm that does not rely on second order techniques, but which does apply different learning rates to each individual weight. According to his comparisons, he concludes that "the additional cost [of stochastic diagonal Levenberg-Marquardt] over regular backpropagation is negligible and convergence is - as a rule of thumb - about three times faster than a carefully tuned stochastic gradient algorithm." (See page 35 of the article.)
It was clear to me that I needed a second order algorithm. Convergence without it was tediously slow. Dr. Simard, in his article titled "Best Practices for Convolutional Neural Networks Applied to Visual Document Analysis," indicated that he wanted to keep his algorithm as simple as possible and therefore did not use second order techniques. He also admitted that he required hundreds of epochs for convergence (my guess is that he required a few thousand).
With the MNIST database, each epoch requires 60,000 backpropagations, and on my computer each epoch took around 40 minutes. I did not have the patience (or confidence in the correctness of the code) to wait for thousands of epochs. It was also clear that, unlike Dr. LeCun, I did not have the skill to design "a carefully tuned stochastic gradient algorithm". So, in keeping with the advice that stochastic diagonal Levenberg-Marquardt would be around three times faster than that anyway, my neural network implements this second order technique.
I will not go into the math or the code for the stochastic diagonal Levenberg-Marquardt algorithm. It's actually not too dissimilar from standard backpropagation. Using this technique, I was able to achieve good convergence in around 20-25 epochs. In my mind this was terrific for two reasons. First, it increased my confidence that the network was performing correctly, since Dr. LeCun also reported convergence in around 20 epochs. Second, at 40 minutes per epoch, the network converged in around 14-16 hours, which is a palatable amount of time for an overnight run.
If you have the inclination to inspect the code on this point, the functions you want to focus on are named CMNistDoc::CalculateHessian() (which is in the document class - yes, the program is an MFC doc/view program), and NeuralNetwork::BackpropagateSecondDervatives(). In addition, you should note that the NNWeight class includes a double member that was not mentioned in the simplified view above. This member is named "diagHessian", and it stores the curvature (in weight space) that is calculated by Dr. LeCun's algorithm. Basically, when CMNistDoc::CalculateHessian() is called, 500 MNIST patterns are selected at random. For each pattern, the NeuralNetwork::BackpropagateSecondDervatives() function calculates the Hessian for each weight caused by the pattern, and this number is accumulated in diagHessian. After the 500 patterns are run, the value in diagHessian is divided by 500, which results in a unique value of diagHessian for each and every weight. During actual backpropagation, the diagHessian value is used to amplify the current learning rate eta, such that in highly curved areas in weight space, the learning rate is slowed, whereas in flat areas in weight space, the learning rate is amplified.
Structure of the Convolutional Neural Network
As indicated above, the program does not implement a generalized neural network, and is not a neural network workbench. Rather, it is a very specific neural network, namely, a five-layer convolutional neural network. The input layer takes grayscale data of a 29x29 image of a handwritten digit, and the output layer is composed of ten neurons of which exactly one neuron has a value of +1 corresponding to the answer (hopefully) while all other nine neurons have an output of -1.
Convolutional neural networks are also known as "shared weight" neural networks. The idea is that a small kernel window is moved over neurons from a prior layer. In this network, I use a kernel sized to 5x5 elements. Each element in the 5x5 kernel window has a weight independent of that of another element, so there are 25 weights (plus one additional weight for the bias term). This kernel is shared across all elements in the prior layer, hence the name "shared weight". A more detailed explanation follows.
Illustration and General Description
Here is an illustration of the neural network:
|
| ||||
| Input Layer 29x29 |
Layer #1 6 Feature Maps Each 13x13 |
Layer #2 50 Feature Maps Each 5x5 |
Layer #3 Fully Connected 100 Neurons |
Layer #4 Fully Connected 10 Neurons |
The input layer (Layer #0) is the grayscale image of the handwritten character. The MNIST image database has images whose size is 28x28 pixels each, but because of the considerations described by Dr. Simard in his article "Best Practices for Convolutional Neural Networks Applied to Visual Document Analysis," the image size is padded to 29x29 pixels. There are therefore 29x29 = 841 neurons in the input layer.
Layer #1 is a convolutional layer with six (6) feature maps. Each feature map is sized to 13x13 pixels/neurons. Each neuron in each feature map is a 5x5 convolutional kernel of the input layer, but every other pixel of the input layer is skipped (as described in Dr. Simard's article). As a consequence, there are 13 positions where the 5x5 kernel will fit in each row of the input layer (which is 29 neurons wide), and 13 positions where the 5x5 kernel will fit in each column of the input layer (which is 29 neurons high). There are therefore 13x13x6 = 1014 neurons in Layer #1, and (5x5+1)x6 = 156 weights. (The "+1" is for the bias.)
On the other hand, since each of the 1014 neurons has 26 connections, there are 1014x26 = 26364 connections from this Layer #1 to the prior layer. At this point, one of the benefits of a convolutional "shared weight" neural network should become more clear: because the weights are shared, even though there are 26364 connections, only 156 weights are needed to control those connections. As a consequence, only 156 weights need training. In comparison, a traditional "fully connected" neural network would have needed a unique weight for each connection, and would therefore have required training for 26364 different weights. None of that excess training is needed here.
Layer #2 is also a convolutional layer, but with 50 feature maps. Each feature map is 5x5, and each unit in the feature maps is a 5x5 convolutional kernel of corresponding areas of all 6 of the feature maps of the previous layers, each of which is a 13x13 feature map. There are therefore 5x5x50 = 1250 neurons in Layer #2, (5x5+1)x6x50 = 7800 weights, and 1250x26 = 32500 connections.
Before proceeding to Layer #3, it's worthwhile to mention a few points on the architecture of the neural network in general, and on Layer #2 in particular. As mentioned above, each feature map in Layer #2 is connected to all 6 of the feature maps of the previous layer. This was a design decision, but it's not the only decision possible. As far as I can tell, the design is the same as Dr. Simard's design. But it's distinctly different from Dr. LeCun's design. Dr. LeCun deliberately chose not to connect each feature map in Layer #2 to all of the feature maps in the previous layer. Instead, he connected each feature map in Layer #2 to only a few selected ones of the feature maps in the previous layer. Each feature map was, in addition, connected to a different combination of feature maps from the previous layer. As Dr. LeCun explained it, his non-complete connection scheme would force the feature maps to extract different and (hopefully) complementary information, by virtue of the fact that they are provided with different inputs. One way of thinking about this is to imagine that you are forcing information through fewer connections, which should result in the connections becoming more meaningful. I think Dr. LeCun's approach is correct. However, to avoid additional complications to programming that was already complicated enough, I chose the simpler approach of Dr. Simard.
Other than this, the architectures of all three networks (i.e., the one described here and those described by Drs. LeCun and Simard) are largely similar.
Turning to Layer #3, Layer #3 is a fully-connected layer with 100 units. Since it is fully-connected, each of the 100 neurons in the layer is connected to all 1250 neurons in the previous layer. There are therefore 100 neurons in Layer #3, 100*(1250+1) = 125100 weights, and 100x1251 = 125100 connections.
Layer #4 is the final, output layer. This layer is a fully-connected layer with 10 units. Since it is fully-connected, each of the 10 neurons in the layer is connected to all 100 neurons in the previous layer. There are therefore 10 neurons in Layer #4, 10x(100+1) = 1010 weights, and 10x101 = 1010 connections.
Like Layer #2, this output Layer #4 also warrants an architectural note. Here, Layer #4 is implemented as a standard, fully connected layer, which is the same as the implementation of Dr. Simard's network. Again, however, it's different from Dr. LeCun's implementation. Dr. LeCun implemented his output layer as a "radial basis function", which basically measures the Euclidean distance between the actual inputs and a desired input (i.e., a target input). This allowed Dr. LeCun to experiment in tuning his neural network so that the output of Layer #3 (the previous layer) matched idealized forms of handwritten digits. This was clever, and it also yields some very impressive graphics. For example, you can basically look at the outputs of his Layer #3 to determine whether the network is doing a good job at recognition. For my Layer #3 (and Dr. Simard's), the outputs of Layer #3 are meaningful only to the network; looking at them will tell you nothing. Nevertheless, the implementation of a standard, fully connected layer is far simpler than the implementation of radial basis functions, both for forward propagation and for training during backpropagation. I therefore chose the simpler approach.
Altogether, adding the above numbers, there are a total of 3215 neurons in the neural network, 134066 weights, and 184974 connections.
The object is to train all 134066 weights so that, for an arbitrary input of a handwritten digit at the input layer, there is exactly one neuron at the output layer whose value is +1 whereas all other nine (9) neurons at the output layer have a value of -1. Again, the benchmark was an error rate of 0.82% or better, corresponding to the results obtained by Dr. LeCun.
Code For Building the Neural Network
The code for building the neural network is found in the CMNistDoc::OnNewDocument() function of the document class. Using the above illustration, together with its description, it should be possible to follow the code which is reproduced in simplified form below:
// simplified code BOOL CMNistDoc::OnNewDocument() { if (!COleDocument::OnNewDocument()) return FALSE; // grab the mutex for the neural network CAutoMutex tlo( m_utxNeuralNet ); // initialize and build the neural net NeuralNetwork& NN = m_NN; // for easier nomenclature NN.Initialize(); NNLayer* pLayer; int ii, jj, kk; double initWeight; // layer zero, the input layer. // Create neurons: exactly the same number of neurons as the input // vector of 29x29=841 pixels, and no weights/connections pLayer = new NNLayer( _T("Layer00") ); NN.m_Layers.push_back( pLayer ); for ( ii=0; ii<841; ++ii ) { pLayer->m_Neurons.push_back( new NNNeuron() ); } // layer one: // This layer is a convolutional layer that // has 6 feature maps. Each feature // map is 13x13, and each unit in the // feature maps is a 5x5 convolutional kernel // of the input layer. // So, there are 13x13x6 = 1014 neurons, (5x5+1)x6 = 156 weights pLayer = new NNLayer( _T("Layer01"), pLayer ); NN.m_Layers.push_back( pLayer ); for ( ii=0; ii<1014; ++ii ) { pLayer->m_Neurons.push_back( new NNNeuron() ); } for ( ii=0; ii<156; ++ii ) { initWeight = 0.05 * UNIFORM_PLUS_MINUS_ONE; // uniform random distribution pLayer->m_Weights.push_back( new NNWeight( initWeight ) ); } // interconnections with previous layer: this is difficult // The previous layer is a top-down bitmap // image that has been padded to size 29x29 // Each neuron in this layer is connected // to a 5x5 kernel in its feature map, which // is also a top-down bitmap of size 13x13. // We move the kernel by TWO pixels, i.e., we // skip every other pixel in the input image int kernelTemplate[25] = { 0, 1, 2, 3, 4, 29, 30, 31, 32, 33, 58, 59, 60, 61, 62, 87, 88, 89, 90, 91, 116,117,118,119,120 }; int iNumWeight; int fm; // "fm" stands for "feature map" for ( fm=0; fm<6; ++fm) { for ( ii=0; ii<13; ++ii ) { for ( jj=0; jj<13; ++jj ) { // 26 is the number of weights per feature map iNumWeight = fm * 26; NNNeuron& n = *( pLayer->m_Neurons[ jj + ii*13 + fm*169 ] ); n.AddConnection( ULONG_MAX, iNumWeight++ ); // bias weight for ( kk=0; kk<25; ++kk ) { // note: max val of index == 840, // corresponding to 841 neurons in prev layer n.AddConnection( 2*jj + 58*ii + kernelTemplate[kk], iNumWeight++ ); } } } } // layer two: // This layer is a convolutional layer // that has 50 feature maps. Each feature // map is 5x5, and each unit in the feature // maps is a 5x5 convolutional kernel // of corresponding areas of all 6 of the // previous layers, each of which is a 13x13 feature map // So, there are 5x5x50 = 1250 neurons, (5x5+1)x6x50 = 7800 weights pLayer = new NNLayer( _T("Layer02"), pLayer ); NN.m_Layers.push_back( pLayer ); for ( ii=0; ii<1250; ++ii ) { pLayer->m_Neurons.push_back( new NNNeuron( (LPCTSTR)label ) ); } for ( ii=0; ii<7800; ++ii ) { initWeight = 0.05 * UNIFORM_PLUS_MINUS_ONE; pLayer->m_Weights.push_back( new NNWeight( initWeight ) ); } // Interconnections with previous layer: this is difficult // Each feature map in the previous layer // is a top-down bitmap image whose size // is 13x13, and there are 6 such feature maps. // Each neuron in one 5x5 feature map of this // layer is connected to a 5x5 kernel // positioned correspondingly in all 6 parent // feature maps, and there are individual // weights for the six different 5x5 kernels. As // before, we move the kernel by TWO pixels, i.e., we // skip every other pixel in the input image. // The result is 50 different 5x5 top-down bitmap // feature maps int kernelTemplate2[25] = { 0, 1, 2, 3, 4, 13, 14, 15, 16, 17, 26, 27, 28, 29, 30, 39, 40, 41, 42, 43, 52, 53, 54, 55, 56 }; for ( fm=0; fm<50; ++fm) { for ( ii=0; ii<5; ++ii ) { for ( jj=0; jj<5; ++jj ) { // 26 is the number of weights per feature map iNumWeight = fm * 26; NNNeuron& n = *( pLayer->m_Neurons[ jj + ii*5 + fm*25 ] ); n.AddConnection( ULONG_MAX, iNumWeight++ ); // bias weight for ( kk=0; kk<25; ++kk ) { // note: max val of index == 1013, // corresponding to 1014 neurons in prev layer n.AddConnection( 2*jj + 26*ii + kernelTemplate2[kk], iNumWeight++ ); n.AddConnection( 169 + 2*jj + 26*ii + kernelTemplate2[kk], iNumWeight++ ); n.AddConnection( 338 + 2*jj + 26*ii + kernelTemplate2[kk], iNumWeight++ ); n.AddConnection( 507 + 2*jj + 26*ii + kernelTemplate2[kk], iNumWeight++ ); n.AddConnection( 676 + 2*jj + 26*ii + kernelTemplate2[kk], iNumWeight++ ); n.AddConnection( 845 + 2*jj + 26*ii + kernelTemplate2[kk], iNumWeight++ ); } } } } // layer three: // This layer is a fully-connected layer // with 100 units. Since it is fully-connected, // each of the 100 neurons in the // layer is connected to all 1250 neurons in // the previous layer. // So, there are 100 neurons and 100*(1250+1)=125100 weights pLayer = new NNLayer( _T("Layer03"), pLayer ); NN.m_Layers.push_back( pLayer ); for ( ii=0; ii<100; ++ii ) { pLayer->m_Neurons.push_back( new NNNeuron( (LPCTSTR)label ) ); } for ( ii=0; ii<125100; ++ii ) { initWeight = 0.05 * UNIFORM_PLUS_MINUS_ONE; } // Interconnections with previous layer: fully-connected iNumWeight = 0; // weights are not shared in this layer for ( fm=0; fm<100; ++fm ) { NNNeuron& n = *( pLayer->m_Neurons[ fm ] ); n.AddConnection( ULONG_MAX, iNumWeight++ ); // bias weight for ( ii=0; ii<1250; ++ii ) { n.AddConnection( ii, iNumWeight++ ); } } // layer four, the final (output) layer: // This layer is a fully-connected layer // with 10 units. Since it is fully-connected, // each of the 10 neurons in the layer // is connected to all 100 neurons in // the previous layer. // So, there are 10 neurons and 10*(100+1)=1010 weights pLayer = new NNLayer( _T("Layer04"), pLayer ); NN.m_Layers.push_back( pLayer ); for ( ii=0; ii<10; ++ii ) { pLayer->m_Neurons.push_back( new NNNeuron( (LPCTSTR)label ) ); } for ( ii=0; ii<1010; ++ii ) { initWeight = 0.05 * UNIFORM_PLUS_MINUS_ONE; } // Interconnections with previous layer: fully-connected iNumWeight = 0; // weights are not shared in this layer for ( fm=0; fm<10; ++fm ) { NNNeuron& n = *( pLayer->m_Neurons[ fm ] ); n.AddConnection( ULONG_MAX, iNumWeight++ ); // bias weight for ( ii=0; ii<100; ++ii ) { n.AddConnection( ii, iNumWeight++ ); } } SetModifiedFlag( TRUE ); return TRUE; }
This code builds the illustrated neural network in stages, one stage for each layer. In each stage, an NNLayer is new'd and then added to the NeuralNetwork's vector of layers. The needed number of NNNeurons and NNWeights are new'd and then added respectively to the layer's vector of neurons and vector of weights. Finally, for each neuron in the layer, NNConnections are added (using the NNNeuron::AddConnection() function), passing in appropriate indices for weights and neurons.
MNIST Database of Handwritten Digits
The MNIST database is modified (hence the "M") from a database of handwritten patterns offered by the National Institute of Standards and Technology ("NIST"). As explained by Dr. LeCun at the MNIST section of his web site, the database has been broken down into two distinct sets, a fist set of 60,000 images of handwritten digits that is used as a training set for the neural network, and a second set of 10,000 images that is used as a testing set. The training set is composed of digits written by around 250 different writers, of which approximately half are high school students and the other half are U.S. census workers. The number of writers in the testing set is unclear, but special precautions were made to ensure that all writers in the testing set were not also in the training set. This makes for a strong test, since the neural network is tested on images from writers that it has never before seen. It is thus a good test of the ability of the neural network to generalize, i.e., to extract intrinsically important features from the patterns in the training set that are also applicable to patterns that it has not seen before.
To use the neural network, you must download the MNIST database. Besides the two files that compose the patterns from the training and testing sets, there are also two companion files that give the "answers", i.e., the digit that is represented by a corresponding handwritten pattern. These two files are called "label" files. As indicated at the beginning of this article, the four files can be downloaded from here (11,594 Kb total).
Incidentally, it's been mentioned that Dr. LeCun's achieval of an error rate of 0.82% has been used as a benchmark. If you read Dr. Simard's article, you will see that he claims an even better error rate of 0.40%. Why not use Dr. Simard's 0.40% as the benchmark?
The reason is that Dr. Simard did not respect the boundary between the training set and the testing set. In particular, he did not respect the fact that the writers in the training set were distinct from the writers in the testing set. In fact, Dr. Simard did not use the testing set at all. Instead, he trained with the first 50,000 patterns in the training set, and then tested with the remaining 10,000 patterns. This raises the possibility that, during testing, Dr. Simard's network was fed patterns from writers whose handwriting had already been seen before, which would give the network an unfair advantage. Dr. LeCun, on the other hand, took pains to ensure that his network was tested with patterns from writers it had never seen before. Thus, as compared with Dr. Simard's testing, Dr. LeCun's testing was more representative of real-world results since he did not give his network any unfair advantages. That's why I used Dr. LeCun's error rate of 0.82% as the benchmark.
Finally, you should note that the MNIST database is still widely used for study and testing, despite the fact that it was created back in 1998. As one recent example, published in February 2006, see:
- Fabien Lauer, Ching Y. Suen and Gerard Bloch, "A Trainable Feature Extractor for Handwritten Digit Recognition", Elsevier Science, February 2006
In the Lauer et al. article, the authors used a convolutional neural network for everything except the actual classification/recognition step. Instead, they used the convolutional neural network for black-box extraction of feature vectors, which they then fed to a different type of classification engine, namely a support vector machine ("SVM") engine. With this architecture, they were able to obtain the excellent error rate of just 0.54%. Good stuff.
Overall Architecture of the Test/Demo Program
The test program is an MFC SDI doc/view application, using worker threads for the various neural network tasks.
The document owns the neural network as a protected member variable. Weights for the neural network are saved to and loaded from an .nnt file in the CMNistDoc::Serialize() function. Storage/retrieval of the weights occurs in response to the menu items "File->Open" and "File->Save" or "Save As". For this purpose, the neural network also has a Serialize() function, which was not shown in the simplified code above, and it is the neural network that does the heavy lifting of storing its weights to a disk file, and extracting them later.
The document further holds two static functions that are used for the worker threads to run backpropagation and testing on the neural network. These functions are unimaginatively named CMNistDoc::BackpropagationThread() and CMNistDoc::TestingThread(). The functions are not called directly; instead, other classes that wish to begin a backpropagation or testing cycle ask the document to do so for them, by calling the document's StartBackpropagation() and StartTesting() functions. These functions accept parameters for the backpropagation or the testing, and then kick off the threads to do the work. Results are reported back to the class that requested the work using the API's ::PostMessage() function with a user-defined message and user-defined codings of the wParam and lParam parameters.
Two helper classes are also defined in the document, named CAutoCS and CAutoMutex. These are responsible for automatic locking and release of critical sections and mutexes that are used for thread synchronization. Note that the neural network itself does not have a critical section. I felt that thread synchronization should be the responsibility of the owner of the neural network, and not the responsibility of the neural network, which is why the document holds these synchronization objects. The CAutoCS and CAutoMutex classes lock and release the synchronization objects through use of well-known RAII techniques ("resource acquisition is initialization").
The document further owns the MNIST database files, which are opened and closed in the CMNistDoc::OnButtonOpenMnistFiles() and CMNistDoc::OnButtonCloseMnistFiles() functions. These functions are button handlers for correspondingly-labeled buttons on the view. When opening the MNIST files, all four files must be opened, i.e., the pattern files for the training and testing sets, and the label files for the training and testing set. There are therefore four "Open File" dialogs, and prompts on the dialogs tell you which file should be opened next.
The view is based on CFormView, and holds a single tab control with three tabs, a first for a graphical view of the neural network and the outputs of each of its neurons, a second for backpropagation and training, and a third for testing. The view is resizable, using an excellent class named DlgResizeHelper, described at Dialog Resize Helper by Stephan Keil.
Each tab on the tab control hosts a different CDialog-derived class. The first tab hosts a CDlgCharacterImage dialog which provides the graphical view of the neural network and the outputs of each neuron. The second tab hosts a CDlgNeuralNet dialog which provides control over training of the neural network, and which also gives feedback and progress during the training process (which can be lengthy). The third tab hosts a CDlgTesting dialog which provides control over testing and outputs test results. Each of these tabs/dialogs is described in more detail in the following sections.
Using The Demo Program
To use the program, you must open five files: four files comprising the MNIST database, and one file comprising the weights for the neural network.
To open the MNIST database files, click the "Open MNist" button at the bottom of the screen. You will be prompted four successive times to open the four files comprising the MNIST database, namely, the training patterns, the label (i.e., the answers) for the training patterns, the testing patterns, and the labels for the testing patterns.
To open the weights for the neural network, from the main menu, choose File->Open, or choose the file-open icon from the toolbar. You will be prompted to open a .nnt file that contains the weights and the structure of the neural network.
Graphical View of the Neural Network
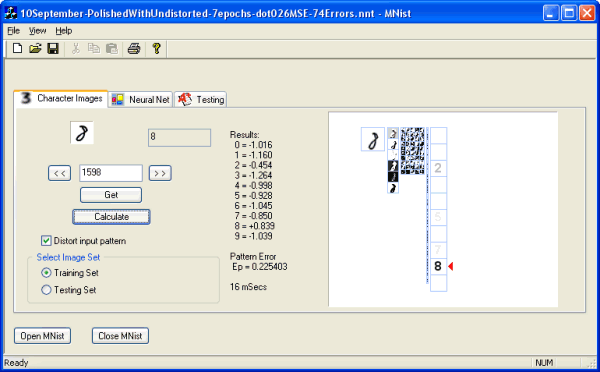
The graphical view of the neural network is the same as the screenshot at the top of this article, and it's repeated again here:

The window at the mid-right shows the output of all 3215 neurons. For each neuron, the output is represented as a single grayscale pixel whose gray level corresponds to the neuron's output: white equals a fully off neuron (value of -1) and black equals a fully on neuron (value of +1). The neurons are grouped into their layers. The input layer is the 29x29 pattern being recognized. Next are the six 13x13 feature maps of the second layer, followed in turn by the 50 5x5 feature maps of the third layer, the 100 neurons of the fourth layer (arranged in a column), and finally the 10 output neurons in the output layer.
Since individual pixels are hard to see clearly, a magnified view is provided. Simply move your mouse over the window, and a magnified window is displayed that lets you see each pixel's value clearly.
The display for the output layer is a bit different than for the other layers. Instead of a single pixel, the 10 output neurons are shown as a grayscale representation of the digit coded by that neuron. If the neuron is fully off (value of -1), the digit is shown as pure white, which of course means that it can't be seen against the white background. If the neuron is fully on (value of +1) then the digit is shown in pure black. In-between values are shown by varying degrees of grayness. In the screenshot above, the output of the neural network shows that it firmly believes that the pattern being recognized is an "8" (which is correct). But the dimly displayed "2" also shows that the neural network sees at least some similarity in the pattern to the digit "2". A red marker points to the most likely result.
The mid-left of the dialog shows the appearance of the pattern at a selectable index. Here the pattern's index is 1598 in the training set. Controls are arranged to allow fast sequencing through the patterns, and to allow selection of either the training set or the testing set. There is also a check box for distortion of the pattern. Distortion helps in training of the neural network, since it forces the network to extract the intrinsic shapes of the patterns, rather than allowing the network to (incorrectly) focus on peculiarities of individual patterns. This is discussed in greater detail below, but in essence, it helps the neural network to generalize. If you look carefully at the screenshot above, you will notice that the input pattern for the digit "8" (on the left) has been slightly distorted when it is given as the input layer to the neural network (on the right).
The "Calculate" button causes the neural network to forward propagate the pattern in the input layer and attempt a recognition of it. The actual numeric values of the output neurons are shown in the center, together with the time taken for the calculation. Although almost all other operations on the neural network are performed in a thread, for recognitions of single patterns, the time taken is so short (typically around 15 milliseconds) that the calculation is performed in the main UI thread.
Training View and Control Over the Neural Network
Unless training is actually ongoing, the training view hides many of its controls. Training is started by clicking on the "Start Backpropagation" button, and during training, the training view looks like the following screenshot:

During training, the 60,000 patterns in the training set are continuously processed (in a random sequence) by the backpropagation algorithm. Each pass through the 60,000 patterns is called an "epoch". The display shows statistics about this process. Starting at the top, the display gives an estimate of the current mean squared error ("MSE") of the neural network. MSE is the value of ![]() in equation (1) above, averaged across all 60,000 patterns. The value at the top is only a running estimate, calculated over the last 200 patterns.
in equation (1) above, averaged across all 60,000 patterns. The value at the top is only a running estimate, calculated over the last 200 patterns.
A history of the current estimate of MSE is seen graphically just to the right. This is a graph of the current estimates of MSE, over the last four epochs.
Just below are a few more statistics, namely the number of fully-completed epochs, and the cardinal number of the current pattern being backpropagated. A progress bar is also shown.
Below that is an edit control showing information about each epoch. The information is updated as each epoch is completed.
The edit control also indicates when the Hessian (needed for second order backpropagation) is being calculated. During this time, which requires an analysis of 500 random patters, the neural network is not able to do much else, so a string of dots slowly scrolls across the control. Frankly, it's not logical to put this display inside the edit control, and this might change in future developments.
Backpropagation can be stopped at any time by clicking the "Stop Backpropagation" button.
Testing View of the Neural Network
The testing view of the neural network is shown in the following screenshot:

In the testing mode, the 10,000 patterns in the testing set are run through the neural network, and if the output of the neural network does not match the expected output, an error is recorded in the view's main edit control. A progress bar through the testing set is displayed, and at the completion of testing, a summary of the total number of errors is displayed.
A testing sequence is commenced by clicking the "Start Testing" button, at which point you are shown a dialog from which you can select the testing parameters:

It's usually best simply to select the default values. The meaning of the available parameters will become clearer once we look at the training parameters in the next section. Note that it is possible to "test" the training set, which can be useful for checking on convergence of the weights.
Training the Neural Network
In order of importance, training is probably the next most important topic after design of the overall architecture of the neural network. We will discuss it over the next few sections.
The idea of training is to force the neural network to generalize. The word "generalization" deserves a few moments of your thought. An enormous amount of time is spent in analyzing the training set, but out in the real world, the performance of the neural network on the training set is of absolutely no interest. Almost any neural network can be trained so well it might not encounter any errors at all on the training set. But who cares about that? We already know the answers for the training set. The real question is, how well will the neural network perform out in the real world on patterns that it has never before seen?
The ability of a neural network to do well on patterns that it has never seen before is called "generalization". The effort spent in training is to force the neural network to see intrinsic characteristics in the training set, which we hope will also be present in the real world. When we calculate the MSE of the training set, we do so with the understanding that this is only an estimate of the number that we are really interested in, namely, the MSE of real-world data.
A few techniques are used during training in an effort to improve the neural network's generalization. As one example, the training set is passed through the neural network in a randomized order in each epoch. Conceptually, these techniques cause the weights to "bounce around" a bit, thereby preventing the neural network from settling on weights that emphasize false attributes of the patterns, i.e., attributes that are peculiar to patterns in the training set but which are not intrinsic characteristics of patterns encountered out in the real world.
One of the more important techniques for improving generalization is distortion: the training patterns are distorted slightly before being used in backpropagation. The theory is that these distortions force the neural network to look more closely at the important aspects of the training patters, since these patterns will be different each time the neural network sees them. Another way of looking at this is that distortions enlarge the size of the training set, by artificially creating new training patterns from existing ones.
In this program, the CMNistDoc::GenerateDistortionMap() function generates a distortion map that is applied to the training patterns (using the CMNistDoc::ApplyDistortionMap() function) during training. The distortion is calculated randomly for each pattern just before backpropagation. Three different types of distortions are applied:
- Scale Factor: The scale of the pattern is changed so as to enlarge or shrink it. The scale factor for the horizontal direction is different from the scale factor for the vertical direction, such that it is possible to see shrinkage in the vertical scale and enlargement in the horizontal scale.
- Rotation: The entire pattern is rotated clockwise or counterclockwise.
- Elastic: This is a word borrowed Dr. Simard's "Best Practices" paper. Visually, elastic distortions look like a gentle pushing and pulling of pixels in the pattern, almost like viewing the pattern through wavy water.
The result of distortions is illustrated in the following diagram, which shows the original of a pattern for the digit "3" together with 25 examples of distortions applied to the pattern:

You can see the effect of the three types of distortions, but to a human viewer, it is clear that each distortion still "looks like" the digit "3". To the neural network, however, the pixel patterns are remarkably different. Because of these differences, the neural network is forced to see beyond the actual pixel patterns, and hopefully to understand and apply the intrinsic qualities that make a "3" look like a "3".
You select whether or not to apply distortions when you click the "Start Backpropagation" button in the training view, at which point you are shown the following dialog which lets you select other training parameters as well:

Besides distortions, this dialog lets you set other parameters for backpropagation. Most notably, you must specify an initial learning rate "eta" and a final learning rate. Generally speaking, the learning rate should be larger for untrained neural networks, since a large learning rate will allow large changes in the weights during backpropagation. The learning rate is slowly decreased during training, as the neural network learns, so as to allow the weights to converge to some final value. But it never really makes sense to allow the learning rate to decrease too much, or the network will stop learning. That's the purpose of the entry for the final value.
For the initial value of the learning rate, never use a value larger than around 0.001 (which is the default). Larger values cause the weights to change too quickly, and actually cause the weights to diverge rather than converge.
Most of the literature on training of neural networks gives a schedule of learning rates as a function of epoch number. Dr. LeCun, for example, recommends a schedule of 0.0005 for two epochs, followed by 0.0002 for the next three, 0.0001 for the next three, 0.00005 for the next four, and 0.00001 thereafter. I found it easier to program a reduction factor that is applied after N recognitions. Frankly, I think it might have been better to listen to the experts, and this might change in the future to a schedule of learning rates. At present, however, at the end of N recognitions (such as 120,000 recognitions which corresponds to two epochs and is the default value), the program simply multiplies the current learning rate by a factor that's less than one, which results in a continuously decreasing learning rate.
The dialog was also written at a naive time of development, when I thought it might be possible to reduce the learning rate within a single epoch, rather than only after an epoch is completed. So, the reduction factor is given in terms of a reduction after N recognitions, rather than after N epochs which would have been more appropriate.
The default values for the dialog are values that I found to work well for untrained networks. The initial learning rate is 0.001, which is rather large and results in good coarse training quickly, particularly given the second order nature of the backpropagation algorithm. The learning rate is reduced by 79.4% of its value after every two epochs. So, for example, the training rate for the third epoch is 0.000794. The final learning rate is 0.00005, which is reached after around 26 epochs. At this point the neural network is well-trained.
The other options in the dialog are discussed below in the "Tricks" section.
Tricks That Make Training Faster
As indicated in the beginning of the article, this project is an engineering work-in-progress, where many different adjustments are made in an effort to improve accuracy. Against that background, training can be a maddeningly slow process, where it takes several CPU hours to determine whether or not a change was beneficial. As a consequence, there were a few things done to make training progress more quickly.
Three things in particular were done: second order backpropagation, multithreading, and backpropagation skipping. The first has been done before, but I have not seen the second and third techniques in any of the resources that I found (maybe they're new??). Each is discussed below.
Second Order Backpropagation Using Pseudo-Hessian
Second order backpropagation is not really a "trick"; it's a well-understood mathematical technique. And it was discussed above in the section on "Second Order Methods". It's mentioned here again since it clearly had the greatest impact on speeding convergence of the neural network, in that it dramatically reduced the number of epochs needed for convergence of the weights.
The next two techniques are slightly different in emphasis, since they reduce the amount of time spent in any one epoch by speeding progress through the epoch. Put another way, although second order backpropagation reduces the overall time needed for training, the next two techniques reduce the time needed to go through all of the 60,000 patterns that compose a single epoch.
Simultaneous Backpropagation and Forward Propagation
In this technique, multiple threads are used to speed the time needed for one epoch.
Note that in general, multiple threads will almost always have a negative impact on performance. In other words, if it takes time T to perform all work in a single thread, then it will take time T+x to perform the same work with multiple threads. The reason is that the overhead of context switching between threads, and the added burden of synchronization between threads, adds time that would not be necessary if only a single thread were used.
The only circumstance where multiple threads will improve performance is where there are also multiple processors. If there are multiple processors, then it makes sense to divide the work amongst the processors, since if there were only a single thread, then all the other processors would wastefully be idle.
So, this technique helps only if your machine has multiple processors, i.e., if you have a hyper-threaded or dual core processor (Intel terminology) or dual processors (AMD terminology). If you do not have multiple processors, then you will not see any improvement when using multiple threads. Moreover, there is absolutely no benefit to running more threads than you have processors. So, if you have a hyperthreaded machine, use two threads exactly; use of three or more threads does not give any advantage.
But there's a significant problem in trying to implement a multi-threaded backpropagation algorithm. The problem is that the backpropagation algorithm depends on the numerical outputs of the individual neurons from the forward propagation step. So consider a simple multi-threaded scenario: a first thread forward propagates a first input pattern, resulting in neuron outputs for each layer of the neural network including the output layer. The backpropagation stage is then started, and equation (2) above is used to calculate how errors in the pattern depend on outputs of the output layer.
Meanwhile, because of multithreading, another thread selects a second pattern and forward propagates it through the neural network, in preparation for the backpropagation stage. There's a context switch back to the first thread, which now tries to complete backpropagation for the first pattern.
And here's where the problem becomes evident. The first thread needs to apply equations (3) and (4). But these equations depend on the numerical outputs of the neurons, and all of those values have now changed, because of the action of the second thread's forward propagation of the second pattern.
My solution to this dilemma is to memorize the outputs of all the neurons. In other words, when forward propagating an input pattern, the outputs of all 3215 neurons are stored in separate memory locations, and these memorized outputs are used during the backpropagation stage. Since the outputs are stored, another thread's forward propagation of a different pattern will not affect the backpropagation calculations.
The sequence runs something like this. First, a thread tries to lock a mutex that protects the neural network, and will wait until it can obtain the lock. Once the lock is obtained, the thread forward propagates a pattern and memorizes the output values of all neurons in the network. The mutex is then released, which allows another thread to do the same thing.
Astute readers will note that this solution might solve the problem of equations (2) through (4), since those equations depend on the numerical values of the neuron outputs, but that this solution does not address additional problems caused by equations (5) and (6). These two equations depend on the values of the weights, and the values of the weights might be changed out from under one thread by another thread's backpropagation. For example, continuing the above explanation, the first thread starts to backpropagate, and changes the values of the weights in (say) the last two layers. At this point, there is a context switch to the second thread, which also tries to calculate equation (5) and also tries to change the values of weights according to equation (6). But since both equations depend on weights that have now been changed by the first thread, the calculations performed by the second thread are not valid.
The solution here is to ignore the problem, and explain why it's numerically valid to do so. It's valid to ignore the problem because the errors caused by using incorrect values for the weights are generally negligible. To see that the errors are negligible, let's use a numeric example. Consider a worst-case situation that might occur during very early training when the errors in the output layer are large. How large can the errors be? Well, the target value for the output of a neuron might be +1, whereas the actual output might be -1 which is as wrong as it can get. So, per equation (2), the error is 2. Let's backpropagate that error of 2. In equation (3) we see that the error is multiplied by G(x), which is the derivative of the activation function. The maximum value that G(x) can assume is around +1, so the error of 2 is still 2. Likewise, in equation (4), the value of 2 is multiplied by the outputs of neurons in the previous layer. But those outputs generally cannot exceed a value of +1 (since the outputs are limited by the activation function). So again, the error of 2 is still 2.
We need to skip equation (5) for a moment, since it's equation (6) that actually changes the values of the weights. In equation (6) we see that the change in the weight is our value of 2 multiplied by the learning rate eta (possibly multiplied by a second order Hessian). We know eta is small, since we deliberately set it to a small value like 0.001 or less. So, any weight might be changed by as much as our value of 2 multiplied by eta, or 2 x 0.001 = 0.002.
Now we can tackle equation (5). Let's assume that the second thread has just modified a weight as described above, which is now 0.002 different from the value that the first thread should be using. The answer here is a big "so what". It's true that the value of the weight has been changed, but the change is only 0.2%. So even though the first thread is now using a value for the weight that is wrong, the amount by which the weight is wrong is completely negligible, and it's justifiable to ignore it.
It can also be seen that the above explanation is a worst-case explanation. As the training of the neural network improves, the errors in each layer are increasingly smaller, such that it becomes even more numerically justifiable to ignore this effect of multithreading.
There's one final note on implementation in the code. Since the program is multithreaded, it cannot alter weights without careful synchronization with other threads. The nature of equation (6) is also such that one thread must be respectful of changes to the value of weight made by other threads. In other words, if the first thread simply wrote over the value of the weight with the value it wants, then changes made by other threads would be lost. In addition, since the weights are stored as 64-bit doubles, there would be a chance that the actual weight might be corrupt if a first thread were interrupted before it had a chance to update both of the 32-bit halves of the weight.
In this case, synchronization is achieved without a kernel-mode locking mechanism. Rather, synchronization is achieved with a compare-and-swap ("CAS") approach, which is a lock-free approach. This approach makes use of atomic operations that are guaranteed to complete in one CPU cycle. The function used is InterlockedCompareExchange64() which performs an atomic compare-and-exchange operation on specified 64-bit values. The function compares a destination value with a comparand value and exchanges it with an exchange value only if the two are equal. If the two are not equal, then that means that another thread has modified the value of the weight, and the code tries again to make another exchange. Theoretically (and unlike locking mechanisms for synchronization), lock-free methods are not guaranteed to complete in finite time, but that's theory only and in practice lock-free mechanisms are widely used.
The code for updating the weight is therefore the following, which can be found in the NNLayer::Backpropagate() function. Note that the code given above in the "Backpropagation" section was simplified code that omitted this level of detail in the interests of brevity:
// simplified code showing an excerpt // from the NNLayer::Backpropagate() function // finally, update the weights of this layer // neuron using dErr_wrt_dW and the learning rate eta // Use an atomic compare-and-exchange operation, // which means that another thread might be in // the process of backpropagation // and the weights might have shifted slightly struct DOUBLE_UNION { union { double dd; unsigned __int64 ullong; }; }; DOUBLE_UNION oldValue, newValue; double epsilon, divisor; for ( jj=0; jj<m_Weights.size(); ++jj ) { divisor = /* a value that depends on the second order Hessian */ epsilon = etaLearningRate / divisor; // amplify the learning rate based on the Hessian oldValue.dd = m_Weights[ jj ]->value; newValue.dd = oldValue.dd - epsilon * dErr_wrt_dWn[ jj ]; while ( oldValue.ullong != _InterlockedCompareExchange64( (unsigned __int64*)(&m_Weights[ jj ]->value), newValue.ullong, oldValue.ullong ) ) { // another thread must have modified the weight. // Obtain its new value, adjust it, and try again oldValue.dd = m_Weights[ jj ]->value; newValue.dd = oldValue.dd - epsilon * dErr_wrt_dWn[ jj ]; } }
I was very pleased with this speed-up trick, which showed dramatic improvements in speed of backpropagation without any apparent adverse effects on convergence. In one test, the machine had an Intel Pentium 4 hyperthreaded processor, running at 2.8gHz. In singly threaded usage, the machine was able to backpropagate at around 13 patterns per second. In two-threaded use, backpropagation speed was increased to around 18.6 patterns per second. That's an improvement of around 43% in backpropagation speed, which translates into a reduction of 30% in backpropagation time.
In another test, the machine had an AMD Athlon 64 x2 Dual Core 4400+ processor, running at 2.21 gHz. For one-threaded backpropagation the speed was around 12 patterns per second, whereas for two-threaded backpropagation the speed was around 23 patterns per second. That's a speed improvement of 92% and a corresponding reduction of 47% in backpropagation time.
As one final implementation note, my development platform is VC++ 6.0, which does not have the InterlockedCompareExchange64() function, not even as a compiler intrinsic. With help from the comp.programming.threads newsgroup (see this thread), I wrote my own assembler version, which I am reproducing here:
inline unsigned __int64 _InterlockedCompareExchange64(volatile unsigned __int64 *dest, unsigned __int64 exchange, unsigned __int64 comparand) { //value returned in eax::edx __asm { lea esi,comparand; lea edi,exchange; mov eax,[esi]; mov edx,4[esi]; mov ebx,[edi]; mov ecx,4[edi]; mov esi,dest; //lock CMPXCHG8B [esi] is equivalent to the following except //that it's atomic: //ZeroFlag = (edx:eax == *esi); //if (ZeroFlag) *esi = ecx:ebx; //else edx:eax = *esi; lock CMPXCHG8B [esi]; } }
Skip Backpropagation for Small Errors
For a decently-trained network, there are some patterns for which the error is very small. The idea of this speed-up trick, therefore, is that for such patterns where there is only a small error, it is frankly meaningless to backpropagate the error. The error is so small that the weights won't change. Simply put, for errors that are small, there are bigger fish to fry, and there's no point in spending time to backpropagate small errors.
In practice, the demo program calculates the error for each pattern. If the error is smaller than some small fraction of the current MSE, then backpropagation is skipped entirely, and the program proceeds immediately to the next pattern.
The small fraction is set empirically to one-tenth of the current MSE. For a pattern whose error is smaller than one-tenth the overall MSE in the prior epoch, then backpropagation is skipped entirely, and training proceeds to the next pattern.
The actual value of the fractional threshold is settable in the program's .ini file. The dialog for setting training parameters asks you to input the current MSE, so that it has some idea of the cut-off point between performing and not performing backpropagation. It advises you to input a small number for the MSE if you are unsure of the actual MSE, since for small MSE's, essentially all errors are backpropagated.
In testing, as the neural network gets increasingly well-trained, I have found that approximately one-third of the patterns result in an error so small that there's no point in backpropagation. Since each epoch is 60,000 patterns, there's no backpropagation of error for around 20,000 patterns. The remaining 40,000 patterns result in an error large enough to justify backpropagation.
On an Intel Pentium 4 hyperthreaded processor running at 2.8gHz, when these two speed-up tricks are combined (i.e., the multithreading speed-up, combined with skipping of backpropagations for patterns that result in a small error), each epoch completes in around 40 minutes. It's still maddeningly slow, but it's not bad.
Experiences In Training the Neural Network
The default values for parameters found on the "Training" dialog are the result of my experiences in training the neural network for best performance on the testing set. This section gives an abbreviated history of those experiences.
Note: I only recently realized that I should have been tracking the overall MSE for both the training set and the testing set. Before writing this article, I only tracked the MSE of the training set, without also tracking the MSE of the testing set. It was only when I sat down to write the article that I realized my mistake. So, when you see a discussion of MSE, it's the MSE of the training set and not the MSE of the testing set.
My first experimentations were designed to determine whether there was a need for distortions while training, or if they just got in the way. Over many epochs without distortions, I was never able to get the error rate in the testing set below around 140 mis-recognitions out of the 10,000 testing patterns, or a 1.40% error rate. To me this meant that distortions were needed, since without them, the neural network was not able to effectively generalize its learned behavior when confronted with a pattern (from the testing set) that it had never before seen.
I am still not able to explain why Dr. LeCun was able to achieve an error rate of 0.89% without distortions. Perhaps one day I will repeat these experiments, now that I have more experience in training the network.
Anyway, having determined that distortions were needed to improve training and generalization, my experimentations turned toward the selection of "good" values for distortions of the training patterns. Too much distortion seemed to prevent the neural network from reaching a stable point in its weights. In other words, if the distortions were large, then at the end of each epoch, the MSE for the training set remained very high, and did not reach a stable and small value. On the other hand, too little distortion prevented the neural network from generalizing its result to the testing set. In other words, if the distortion was small, then the results from the testing set were not satisfactory.
In the end, I selected values as follows. Note that the values of all tune-able parameters are found in the .ini file for the program:
- Maximum scale factor change (percent, like 20.0 for 20%) = 15.0
- Maximum rotational change (degrees, like 20.0 for 20 degrees) = 15.0
- Sigma for elastic distortions (higher numbers are more smooth and less distorted; Simard uses 4.0) = 8.0
- Scaling for elastic distortions (higher numbers amplify distortions; Simard uses 0.34) = 0.5
Once these values were selected, I began to concentrate on the training progression, and on the influence of the learning rate eta. I set up a 24-hour run, starting from purely randomized weights, over which 30 epochs were completed. The training rate was varied from an initial value of 0.001 down to a minimum of 0.00001 over 20 epochs, and thereafter (i.e., for the final 10 epochs) was maintained at this minimum value. After training was completed, I ran the testing set to see how well the neural network performed.
The results were a very-respectable 1.14% error rate in the set of testing patterns. That is, in the 10,000 pattern testing set, of which the neural net had never before seen any of the patterns, and had never before even seen the handwriting of any of the writers, the neural network correctly recognized 9,886 patterns and incorrectly misrecognized only 114 patterns. For the set of training patterns, there were around 1880 mis-recognitions in the distorted patterns.
Naturally, although I was pleased that the neural network worked at all, I was not satisfied with this performance. Seven years earlier, Dr. LeCun had achieved an error rate of 0.82%. Certainly, given the passage of seven years, better results could be obtained.
So, I graphed backpropagation progress as a function of epoch. At each epoch, I graphed the learning rate eta, the MSE (of the training set), and the change in MSE relative to the previous epoch. Since the change in MSE bounced around a bit, I also graphed a smoothed version of delta MSE. Here are the results. Note that the right-hand axis is for MSE, whereas the left-hand axis is for everything else.

The graph shows very clearly that the neural network reaches a constant MSE quickly, after around 12-15 epochs, and then does not improve any further. The asymptotic value of MSE was 0.135, corresponding to around 1880 mis-recognized patterns in the distorted training set. There was no significant improvement in the neural network's performance after 12-15 epochs, at least not for the learning rates that were used for the latter epochs.
My first reaction, given the asymptotic nature of the curve, was one of concern: maybe the neural network was incapable of learning any better than this. So, I restarted the training with the initial learning rate of 0.001. But this time, instead of starting from purely random weights, I used the weights that resulted from the first 30 epochs. After another 15 hours of training, here is the graph of results:

This graph was reassuring, since it showed that the neural network still had the capability to learn. It was simply a matter of teaching it correctly. At this point, the neural network had settled in on an MSE of around 0.113, corresponding to around 1550 mis-recognized patterns in the distorted training set. For the testing set, there were 103 mis-recognized patterns out of 10,000, which is an error rate of 1.03%. At least there was some improvement, which meant that the neural network could learn more, but not much improvement.
Looking at the graph, I decided that the learning rate should be set to a value that would allow the neural network to improve at a slow but deliberate pace. Arbitrarily, I tried a constant learning rate of 0.00015, which (as seen in the above graph) should have allowed the neural network to improve around 0.01 MSE every three or so epochs. More specifically, looking at the "Smoothed Delta MSE" graph above, at a learning rate of around 0.00015, the delta MSE per epoch was around 0.0033, which should have translated to an improvement of around 0.01 MSE after every three epochs.
The results were miserable. As shown in the following graph, even after an additional 15 epochs at the carefully chosen constant learning rate of 0.00015, there was no noticeable improvement in the network. For the set of training patterns, there were still around 1550 mis-recognized patterns; for the set of testing patterns, there was a slight improvement to 100 errors, for an error rate of exactly 1.00%:

I was not certain of why the neural network failed to improve. Clearly the learning rate was too small, given the small size of the errors being produced by the network, which after all, had decent performance. So, I decided to increase the learning rate to a much larger value. I abandoned the idea of trying to estimate the change in MSE as a function of learning rate, and arbitrarily chose a starting value of eta = 0.0005. It was also clear that the minimum learning rate of 0.00001, used previously, was too small; instead, I chose a minimum learning rate of 0.0002.
On the other hand, I thought that I might be rushing the neural network, in the sense that I had been decreasing the learning rate after each and every epoch. After all, the training patterns were distorted; as a consequence, the neural network never really saw the same training pattern twice, despite the fact that the same patterns were used for all epochs. I decided to let the neural network stick with the same training rate for four epochs in a row, before decreasing it. This produced good results:

As seen in the above graph, the neural network continued to learn for at least 15-20 epochs. The final MSE was somewhere around 0.102, corresponding to around 1410 mis-recognized characters in the distorted training set. On the testing set, there were only 94 errors (an error rate of 0.94%), so I had finally crossed the 1.00% threshold, and could see the possibility of meeting or exceeding the benchmark performance of Dr. LeCun's implementation.
But it had taken many, many epochs to get here. And each training cycle (except the first) had started with an already-trained network. I decided it was time to check whether the results could be reproduced, starting again from scratch, i.e., a blank neural network with purely random weights.
I again chose an initial learning rate of 0.001, but in keeping with the experiences to date, chose a minimum learning rate of 0.00005 (which is five times larger than the minimum learning rate in the first experiment). I also used a stepped decrease in the learning rate, as above, where the learning rate was kept at the same value for 4 epochs before it was reduced. I frankly did not like the math when these parameters were multiplied together: It would take 52 epochs to reach the minimum learning rate, and at 40 minutes per epoch, that would require at least 35 hours of processing time. (Because of the timing of overnight runs, I actually let it run for 63 epochs, or 42 hours.) I bit the bullet, hit the "Backpropagate" button, and waited. The results showed something interesting:

First off, it should be apparent that the network trained itself well. The final MSE for the training set settled in at around 0.102, corresponding to around 1440 mis-recognitions in the distorted patterns of the training set. More importantly, mis-recognitions for the testing set were quite good: there were only 86 mis-recognitions out of the 10,000 patterns in the testing set, for an error rate of 0.86%. Dr. LeCun's benchmark was in sight.
The interesting thing about the graph is the "bump" in the MSE that seems to appear after each time that the learning rate is decreased. Look carefully: there's a kind of periodicity to the "Delta MSE" curve, with a spike (which represents a good reduction in MSE) occurring right after the learning rate is decreased. I theorized that the neural network needs to see the same learning rate for more than one epoch, but does not need to see it for as many as four epochs. After more experimentation, I concluded that the learning rate needs to be constant for only two epochs. This is good news for training, since it means that the neural network can be trained, reproducibly from scratch, to sub-one-percent errors in less than around 15-18 hours.
All together, based on the above experimentation, these are the defaults that you see in the "Backpropagation" dialog:
- Initial learning rate (eta) = 0.001
- Minimum learning rate (eta) = 0.00005
- Rate of decay for learning rate (eta) = 0.794183335
- Decay rate is applied after this number of backprops = 120000
The 0.86% error rate obtained above is very good, but it's still not as good as the 0.74% error rate in the title of this article. How did I get the error reduced further?
After some reflection on the results obtained so far, it appeared to me that there was still an apparent paradox in the error rates. On the training set, which the neural network actually sees, over and over again with only slight distortions, the network was not able to perform better than 1440 mis-recognitions out of 60,000 patterns, which works out to an error rate of 2.40%. That's nearly three times larger than the error rate of 0.86% for the testing set, which the neural network had never even seen. I theorized that while the distortions were clearly needed to force the neural network to generalize (remember: without distortions I was not able to achieve anything better than a 1.40% error rate on the testing set), after a while, they actually hampered the ability of the neural network to recognize and settle in on "good" weights. In a sense, the network might benefit from a final "polishing" with non-distorted patterns.
That's exactly what I did. First I trained (as above) with the distorted training set until I had obtained an error rate of 0.86% on the testing set. Then, I set the learning rate to a constant value of 0.0001, which is small but is still twice as large as the minimum value of 0.00005. At this learning rate, I ran non-distorted training patterns for five "polishing" epochs. The selection of five epochs was somewhat arbitrary/intuitive: at five epochs, the neural network showed 272 errors out of the 60,000 patterns in the training set, for an error rate of 0.45%. This value for error rate seemed appropriate, since it was smaller than the error rate on the testing set, yet not so small that all of the good generalizations introduced by distortions might be undone.
The "polishing" worked well, and resulted in the 0.74% error rate advertised above.
Results
All 74 errors made by the neural network are shown in the following collage. For each pattern, the sequence number is given, together with an indication of the error made by the network. For example, "4176 2=>7" means that for pattern number 4176, the network misrecognized a 2, and thought it was a 7:

For some of these patterns, it's easy to see why the neural network was wrong: the patterns are genuinely confusing. For example, pattern number 5937, which is purported to be a 5, looks to me like a 3, which is what the neural network thought too. Other patterns appear to have artifacts from pre-processing by the MNIST authors, and it's the presence of these artifacts that confused the network. For example, pattern number 5457, which is clearly a 1, also has artifacts on the right-hand side, possibly caused when the pattern was separated from an adjacent pattern. Other patterns, primarily in the 8's, have too much missing from the bottom of the patterns.
But for the vast majority, the neural network simply got it wrong. The patterns aren't especially confusing. Each of the 7's looks like a 7, and there's no good reason why the neural network failed to recognize them as 7's.
Perhaps more training, with a larger training set, would help. I'm inclined to believe, however, that the network is at a point of diminishing returns with respect to training. In other words, more training might help some, but probably not much.
Instead, I believe that a different architecture is needed. For example, I think that the input layer should be designed with due recognition for the fact that the human visual system is very sensitive to spatial frequency. As a result, I believe that better performance could be obtained by somehow converting the input pattern to a frequency domain, which could be used to supplement the purely spatial input now being given as input.
Bibliography
Here, in one place, is a list of all the articles and links mentioned in the article, as well as a few extra articles that might be helpful. Clicking the link will open a new window.
- List of publications by Dr. Yann LeCun
- Section of Dr. LeCun's web site on "Learning and Visual Perception"
- Microsoft's "Document Processing and Understanding" group
- List of publications by Dr. Patrice Simard
- Database of handwritten patterns offered by the National Institute of Standards and Technology ("NIST")
- Modified NIST ("MNIST") database (11,594 Kb total)
- Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner, "Gradient-Based Learning Applied to Document Recognition," Proceedings of the IEEE, vol. 86, no. 11, pp. 2278-2324, Nov. 1998. [46 pages]
- Y. LeCun, L. Bottou, G. Orr, and K. Muller, "Efficient BackProp," in Neural Networks: Tricks of the trade, (G. Orr and Muller K., eds.), 1998. [44 pages]
- Patrice Y. Simard, Dave Steinkraus, John Platt, "Best Practices for Convolutional Neural Networks Applied to Visual Document Analysis," International Conference on Document Analysis and Recognition (ICDAR), IEEE Computer Society, Los Alamitos, pp. 958-962, 2003.
- Fabien Lauer, Ching Y. Suen and Gerard Bloch, "A Trainable Feature Extractor for Handwritten Digit Recognition", Elsevier Science, February 2006
DlgResizeHelperclass, by Stephan Keil, described at Dialog Resize HelperInterlockedCompareExchange64()function on the comp.programming.threads newsgroup
License and Version Information
The source code is licensed under the MIT X11-style open source license. Basically, under this license, you can use/modify the code for almost anything you want. For a comparison with the BSD-style license and the much more restrictive GNU GPL-style license, read this Wikipedia article: "BSD and GPL licensing".
Version information:
- 26 November 2006: Original release of the code and this article.





