Introduction
In
our effort to design a new algorithm for factoring semi-primes, we turn our
attention to the Goldbach conjecture. The conjecture states that any even
number greater or equal to 4 can be represented as the sum of two primes. We
may refine the conjecture by stating that any even number greater or equal to 8
can be represented as the sum of two primes distinct. We can then define the
maximum Goldbach partition (maxGB) as the product of the largest two distinct
primes that sum to the even number e=p+q. We note that e can factor n=p*q by
way of Quadratic equation. There is also the minimum Goldbach partition (minGB)
which is the product of the least two distinct primes that sum to the even
number e=p+q.
Background
Initial
attempts at developing an algorithm utilizing both partitions resulted in
failure. By graphing the output of minGB and maxGB, we see that the data for
minGB is almost random, while maxGB is almost a smooth curve. Our attention
then immediately turned to using a binary search on the maxGB partitions in
order to approximate e=p+q for a given n=p*q. Below is the graph of the data:
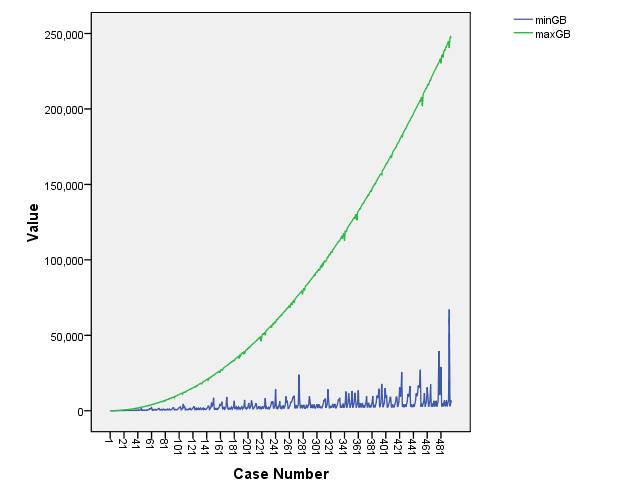
With this, our
approximation of e for a given n became:
bool Q(unsigned long long n, unsigned long long e, unsigned long long *p,
unsigned long long *q)
{
unsigned long long p_q = (unsigned long long)sqrt((e * e) - (4 * n));
*p = (e - p_q) / 2;
*q = (e + p_q) / 2;
if((*p * *q) == n) {
return true;
}
return false;
}
unsigned long long f(unsigned long long n, unsigned long long min, unsigned long long max)
{
unsigned long long e = 0, p = 0, q = 0, p_e = 0, tmp = 0;
if((min%2)) { min++; }
if((max%2)) { max++; }
while(min < max) {
e = (min + max) / 2;
if((e % 2) == 1) e++;
if(p_e == e) {
return e;
}
tmp = maxGB(e);
if(tmp > n) {
max = e - 1;
}
if(tmp < n) {
min = e + 1;
}
if(tmp == n) {
Q(n,e,&p,&q);
return e;
}
if(Q(n,e,&p,&q)) {
return e;
}
p_e = e;
}
return e;
}
Where f is our
approximation logic and Q is our Quadratic equation logic for factoring n. A
caller of f would do the following:
unsigned long long e = f(n,2,n+1);
The logic would
then try to find an approximation for what e=p+q may be. We note that the
algorithm is a binary search algorithm and therefore runs in O(logN) time.
maxGB is defined as:
unsigned long long maxGB(unsigned long long i)
{
unsigned long long t = i / 2, s = t;
while(t) {
t--;
s++;
if(is_prime(t) && is_prime(s) && ((s + t) == i)) {
return t * s;
}
}
return 0;
}
Using the Code
The
code is designed to run as a standalone command line tool. Calling function f
on a given semi-prime n produces an approximation of e=p+q which can be used as
a starting point to find the real value and therefore factor n.
Testing
of the algorithm using a set of pseudo-random generated semi-primes produces
results that look promising. In particular, comparing the algorithm to the
output of Pollard-Rho on those semi-primes shows that Pollard-Rho required much
more iterations in order to factor. In some cases, Pollard-Rho failed to factor
the semi-primes, while in all cases, our algorithm worked successfully and
rather quickly.
There
are limitations here when handling large semi-primes and the algorithm was only
tested on 64bit semi-primes. Large semi-primes require that methods such as
‘is_prime’ use a probabilistic approach rather than trial division.
Multi-threading may be used to help in finding the actual number e for larger
semi-primes. An example run of the algorithm:
$ ./maxGB 55594832159
factored: e=471744 p=229487 q=242257 trials=86
Shows that it took
86 trials to factor the number while factoring using Pollard-Rho took:
$ ./prho.exe 55594832159
factored: n=55594832159 p=242257 q=229487 trials=5783
5783 and that these
results were consistently seen while factoring 32bit and 64bit semi-primes. In
comparing the two algorithms, we factored 1024 32bit+ semi-primes. For
Pollard-Rho, we were successful for 788 cases and failed for 236 cases. We were
successful in factoring all cases using our algorithm. Additionally, the
average number of trials for Pollard-Rho was 26766 while for our algorithm it
was 916, a factor of about 29 faster. Further research is needed to test the
algorithm on larger semi-primes.
Points of
Interest
It
would be interesting to develop the algorithm for large scale semi-primes and
test to see how well it factors larger numbers. At the time of this writing, no
test has been done for large scale numbers. The algorithm would need to have a
probabilistic algorithm for determining if a number is prime and usage of the
built-in integer classes would have to be replaced with an arbitrary precise
type. In testing with 32 bit and 64 bit semi-primes, the code appeared to
perform better than Pollard-Rho. The latter algorithm was used as a bench mark.
