PATRICIA trie implementation

• Download source files - 5.78 Kb
• Download demo project - 462 Kb

Introduction

One thing that .NET is lacking is data structures. Besides arrays, collections and dictionaries, not much effort has been put in this area. That's a pity because most often than not, a judicious choice of a data structure can make a drastic difference in both time and space complexity. Tree-based data structures are amongst the most interesting and it's one of them I chose to explore in this article.

The following description is based on this excellent article by R. Reyes.

Tries are a kind of tree where each node holds a common part of one or more keys. As an example, for a trie holding strings, the words "eater" and "eating" would be stored as follows:

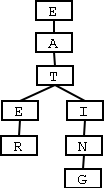
One of the many existing variants of the trie is the PATRICIA trie (Practical Algorithm To Retrieve Information Coded In Alphanumeric), which adds path compression by grouping common sequences of nodes together:

This structure provides a very efficient way of storing values while maintaining the lookup time for a key in O(N) in the worst case, where N is the length of the longest key. This structure has it's main use in IP routing software, but can provide an interesting alternative to other structures such as hashtables when memory space is of concern.

Demo: mapping of IPs to ISO3166 country codes

The demo project contains an actual useful use of tries:

First, it will build a trie with the mapping of IP masks to country codes (about 50000 IP masks).

It will then lookup the country associated to 25000 IP and give the time taken to do so, along with the relative speed measured in IP/sec.

If you want, you can easily take the 3 classes that do the actual work (IPCountryLookupTable, Trie and TrieNode) and build a simple application that will retrieve the country code of an IP or a batch of IP.

The implementation

Before designing and coding the classes, I set myself these goals:

• Simplicity of use
• High speed and memory optimization
• Powerful set of features
• Ease of extension and addition of new implementations

This implementation is a numeric PATRICIA trie. That is, a trie that can only hold 32 bit integers (signed or not). However, I designed the code with the goal of making at least two additional implementations:

• Variable length strings
• Big numbers (any base up to 36)

To ensure consistency amongst all types of tries, I made two interfaces, ITrie and ITrieNode, defining the basic capacities of a trie and its nodes.

The reason behind this choice as a first implementation is simply because I got myself into writing this article upon looking at the following projects, which both required this kind of trie:

• Optimized IP to ISO3166 Country Code Mapping in C# by R. Reyes
• Extreme Optimization #1: Mapping IP addresses to country codes by Jeffrey Sax

The current implementation supports:

• IList (incl. IEnumerator)
• ICloneable
• Serialization
• Merging one trie into another one
• Creating a new trie by merging two other tries
• Testing for equality (does both tries have the same content?)
• Finding both approximate and exact matches

The classes are highly optimized and memory efficient, even though I think there is always room for improvement in those matters :)

Using the code

The code is well documented, so I will simply provide a quick example showing the capacities of the Trie class and the simplicity of its use.

// Creates a new trie

Trie trie1 = new Trie();

// Adds the key 123 to the trie and indicates

// that we want it stored as a 32-bits wide key

trie1.Add(123, 32);

// Adds again 123, but this time, the key is 16 bits wide.

trie1.Add(123, 16);

// That means we now have two *different* values in the trie :

// (123, 32) : 0000 0000 0000 0000 0000 0000 0111 1011

// (123, 16) : 0000 0000 0111 1011


// Now let's print those keys to the console

foreach (Int32 key in trie1)
    Console.WriteLine(key);

// If you want to associate some data with the key

// just inserted, you can do it when adding the key

TrieNode node = trie1.Add(1234, 32);
node.Data = 
  "Data is of type object, so anything can be put there.";

// Or later if you wish

trie1[1234] = "This is streching the meaning of " + 
             "indexer a bit, but it is quite convenient.";

// This is how you retrieve keys and put them into an array

Int32[] keys;
trie1.GetKeys(out keys);

// And if you want also the key lengths

Int32[] keyLengths;
trie1.GetKeys(out keys, out keyLengths);

// If you want to use an existing array,

// starting at a specified index

// (the array must be large enough to hold all keys)

trie1.GetKeys(ref keys, 0);

// Even simpler, with IList.CopyTo()

trie1.CopyTo(keys, 0);

// Or again, with key lengths this time

trie1.GetKeys(ref keys, ref keyLengths, 0);

// You can also fill an IList with the keys

// and optionally clearing it before processing

ArrayList keyList = new ArrayList();
trie1.GetKeys(keyList, true);

// If you now want to remove the "123" key, which is 16 bits wide

trie1.Remove(123, 16);

// Let's create another trie with some keys in it

Trie trie2 = new Trie();

for (Int32 i = -10; i < 10; i++)
    trie2.Add(i, 32);

// Let's create yet another trie which will be

// the result of the merging of trie1 and trie2

Trie trie3 = Trie.Merge(trie1, trie2);

// If you want to directly merge trie2 into trie1, do it this way

trie1.Merge(trie2);

// You may also want to simply clone a trie (deep cloning)

Trie clone = trie1.Clone();

// If you want to test if a trie contains a key,

// simply use one the IList.Contains() overrided methods

bool result = trie1.Contains(9);
result = trie1.Contains(9, 32);

// If you want to find the best match for a key

// that is, the deepest possible node on the path matching the key

node = trie1.FindBestMatch(1239, 32); 
// node now hold the node corresponding to

// the key 1234 as it is the best match


// If you want to find the *exact* match for a key

node = trie1.FindExactMatch(1239, 32); 
// node is now null because 1239 was not found


// Finally, if you want to clear a trie, simply write

trie1.Clear();

Related articles

• Optimized IP to ISO3166 Country Code Mapping in C# by R. Reyes
• Extreme Optimization #1: Mapping IP addresses to country codes by Jeffrey Sax