
Introduction
A Treap is an efficient general purpose data structure. It has the
characteristics of both a binary search tree (see figure 1) and a heap ordered
priority queue (see figure 2).
Since the efficiency of tree traversal is dependent on the tree's height, a
balanced tree (in which the left and right subtrees of any node are of the same
height) is more more efficient than an unbalanced one (see figure 3).
A Treap is an ordered, binary search tree that balances its nodes using a key
and a random number priority attribute (figure 4). The nodes are first ordered
so that every node's left subtree key has values less than the node's key, and
every right subtree has values greater than the node's key. The nodes are then
reordered by priority according to the minimum heap order (priority queue)
property which implies that the priority value at the node is less than (or
equal) to the priority value of both the left and right child subtrees (if they
are not empty).
The result is a data structure that performs reasonably well. Because it's a
balanced tree, a node is never more than about log n steps away.
Background
The Treap was devised by C. R. Aragon and R. Seidel and described in
Randomized Search Trees (Algorithmica, 16(4/5):464-497, 1996). I
discovered the Treap while looking for a more efficient data structure than the
hash table provided by Java, several years ago. During my search, I found Stefan
Nilsson's Treaps in Java article in Dr. Dobb's Journal (pp. 40-44, Vol.
267, July 1997) and adapted his Treap for my particular use. Stefan has an
online article entitled Treaps in Java.
Using the code
The project available for download includes a Test project that gives
examples calling Treap. Extract the zip file into a directory of your choice.
The zipped file will create its own directory called TreapCS.
The Treap project consists of four classes:
Treap: The main class that implements the Treap API and
functionality.
TreapEnumerator: Returns the keys or data objects of the
Treap in sorted order.
TreapException: Distinguishes Treap exceptions
from .NET exceptions.
TreapNode: Encapsulates a node in the Treap;
performs the rotations to balance the Treap.
After including the TreapCS.DLL as a Reference to the calling project,
using the Treap is similar to using the .NET
HashtTable class.
To create a Treap, call the default constructor:
Treap treap = new Treap();
Like the HashTable, the Treap's Add
method requires a key and data object passed as arguments.
Public Sub Add(ByRef key As IComparable, ByRef data As Object)
The key reference can be a standalone object or embedded within the data
object. The Test project includes samples of both.
In order for the Treap to make the necessary key comparisons,
the key object must implement the .NET IComparable interface:
public class MyKey : IComparable
{
private int intMyKey;
public int Key
{
get
{
return intMyKey;
}
set
{
intMyKey = value;
}
}
public MyKey(int key)
{
intMyKey = key;
}
public int CompareTo(object key)
{
if(Key > ((MyKey)key).Key)
return 1;
else
if(Key < ((MyKey)key).Key)
return -1;
else
return 0;
}
}
Calling the GetData() method passing a key object as an argument
retrieves a data object from the tree.
public object GetData(IComparable key)
Nodes are removed by calling the Remove() method.
public void Remove(IComparable key)
Additionally, the RedBlack class contains several other methods that offer
convenient functionality.
GetMinKey(): Returns the minimum key value.
GetMaxKey(): Returns the maximum key value.
GetMinValue(): Returns the object having the minimum key value.
GetMaxValue(): Returns the object having the maximum key value.
GetEnumerator(): Returns a RedBlackEnumerator used to iterate
through the Treap.
Keys(): Returns a RedBlackEnumerator used to iterate through the keys.
Values(): Returns a RedBlackEnumerator used to iterate through the data
objects.
RemoveMin(): Removes the node with the minimum key.
RemoveMax(): Removes the node with the maximum key.
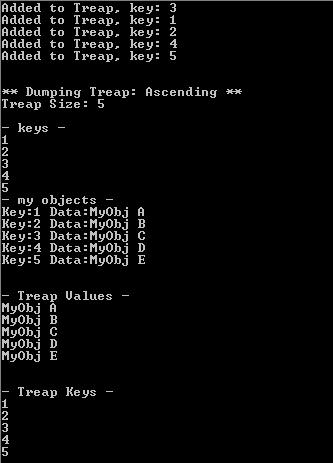
Partial Output from the Test Project
The sample project demonstrates various method calls to the
Treap and displays the effect of the calls dumping the
Treap's contents to the Console. Executing the sample project
produces the following partial output:
Improvements
There's lots of room for improvement in performance, usability, and
functionality. For example, no method exists to determine if a particular key is
present in the Treap. The source is included in the download for
your use to modify as you see fit.
Also, the code makes use of recursion in several methods. You might choose to
remove the recursive calls to increase performance. I sort of like recursion,
but, of course, there're tradeoffs between speed and clarity for a recursive vs.
an iterative implementation.
Points of Interest
For a VB.NET implementation of the Treap, see: Treaps in VB.NET.
The following link contains an excellent animation of a Treap: Randomized Binary Search Trees.
