Heap Data Structure and Heap Sort

and state its properties in the concise form:

h_k >= h_2k+1
h_k >= h_2k+2

1 - heap properties

Now, suppose we have the partial heap

where the top node is missing. If we add an arbitrary value, say 4, the resulting tree is no more a heap,

because the top value is less than its childrens.

However, there is an ingenious way to rearrange the tree in order to get back a heap. Its called sift down of the item and it is shown in the following pictures:

2 - sift down of the item, until the heap is restored

That is, if the parent value is less than any of its children, it is swapped with the greatest child, repeatedly.

Building the Heap in an Array

It is worth noting we can host a heap inside an array.

provided the heap properties (1) hold.

The Algorithm

Starting with an assigned array, we may rearrange it to host an heap, in place, using an algorithm due to R.W.Floyd (see [1]).

Suppose we have the following, arbitrarily assigned, array

The right half side (the blue marked side) is already arranged as the bottom row of a heap, because its items have no children: consider, for instance the first 'blue' item, having value 24. Its index is 7, hence the heap properties for such item (h₇>= h₁₅, h₇>= h₁₆) are automatically satisfied, because there are no items with index 15 or 16 in the array.

So the 'blue side' is our partial heap and we can proceed with heap construction by repeatedly sifting down the items of the 'red side'.

3 - sifting down the first 'red' (left side) item of the array

4 - partial heap is augmented, after having sifted down the item

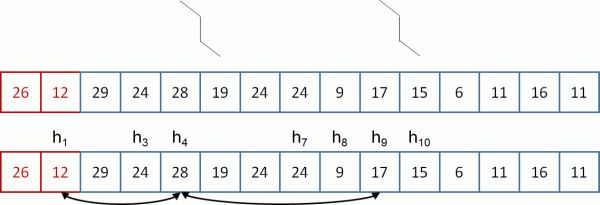
5 - final steps of in place heap construction

I hope these drawings help to understand the algorithm, anyway we cannot run pictures, so it is time to show some code.

The C Code

The sift function is as follows:

// The sift function:
// 'sifts down' the a[l] item until heap properties are restored
// ARGS:
//  a[] (INOUT) the array  (where a[l+1], a[l+2] .. a[size-1] is a partial heap)
//  size (IN) number of items of a
//  l (IN) index of the item inserted into the heap

void sift(int a[], int size, int l)
{
  int i,j, x;
  i = l;
  j = 2*i+1;
  x = a[i];
  while (j < size)
  {
    if ( j <size - 1)
      if ( a[j] < a[j+1])
        ++j;
    if (x >= a[j])
      break;
    a[i] = a[j];
    i = j;
    j = 2*i + 1; // sift
  }
  a[i] = x;
}

The make_heap function is as follows:

// makes the heap using the R.W.Floyd's algorithm
// ARGS:
//  a[] (INOUT) the array wherein the heap is created
//  size (IN) the size of the array
 
void make_heap(int a[], int size)
{
  int l = size / 2;
  while (l)
  {
    --l;
    sift(a, size, l);
  }
} 

That's all.

The Lua Code

The sift function is as follows:

--// sifts the a[k] item in the a[k+1], a[k+2], .., a[r] partial heap
--//
--// REMARKS
--// if r is not provided then r = #a 

local function sift(a, k, r)
  r = r or #a
  local i = k
  local j = 2 * i
  local x = a[i]
  while j <= r do
    if j < r then
      if a[j] < a[j+1] then j = j + 1 end
    end
    if x >= a[j] then break end
    a[i]  = a[j]
    i = j
    j = 2* i
  end
  a[i] = x
end

The make_heap function is as follows:

--// makes a in-place heap in a table using the R.W.Floyd's algorithm

function make_heap(a)
  local l = math.floor(#a/2) + 1
  while l > 1 do
    l = l - 1
    sift(a,l)
  end
end

Heap Sort

Heap sort is one of the nice applications of the data structure and algorithms depicted so far.

Suppose we have an assigned, unsorted array

our task is: sort it in descending order.

We already know how to make a heap with it

so that the maximum value (29) is now the first item of the array (or, in other words, is on the top of the heap).

We can remove such maximum value (storing it in a safe place) and rearrange the remaining items in order to regain a heap (to obtain another 'maximum', that is the successive value of the sorted sequence).

It turns out the safe place for storing the maximum value is the last item of the array. As matter of fact, we swap the first and last item.

Now we have:

• The maximum value in its own safe place (grayed, on the right side of the array)
• A partial heap to fix (the blue items)
• An item to sift down (the read one)

Here, we have back a (one item shorter) heap and can proceed with next items:

Done!

Well, there is just a little problem: our target was: sort it in descending order. Hence, we either re-state it according to our results ( :-) ) or, better, change the algorithm to obtain the opposite sort order. It turns out that just reversing the operators (while comparing array items in the sift function) does the trick (task left to the reader) .

Heap Sort C Code

void heapsort(int a[], int size)
{
  int l = 0, r = size;
  make_heap(a, size);
 
  while ( r > 1)
  {
    int tmp = a[0];
    --r;
    a[0] = a[r];
    a[r] = tmp;
    sift(a, r,0);
  }
}

Heap Sort Lua Code

--// sorts in-place the table 'a'
function heapsort(a)
  make_heap(a)
  local l,r
  l = 1
  r = #a
  while r > 1 do
    local x
    x = a[1]
    a[1] = a[r]
    a[r] = x
    r = r - 1
    sift(a,l,r)
  end
end

References

• 1 Wirth Nicklaus, "Algorithms + Data Structures = Programs".

History

• 28 Feb 2014 - First release