Introduction
Unit test frameworks have been available for the last decade, and provide a fairly uniform way of representing tests, and have a large number of features in common. This can hardly surprise as these frameworks have been built to support the same concept of unit testing. Enter Quality Gate One Studio (QS), which has been built with integration testing in mind, including performance testing and usage model testing, and aims to solve a very different problem.
Background
Wikipedia gives the following definitions of unit and integration testing:
Unit testing is a method by which individual units of source code are tested to determine if they are fit for use. A unit is the smallest testable part of an application. In procedural programming, a unit may be an individual function or procedure [...] Ideally, each test case is independent from the others: substitutes like method stubs, mock objects, fakes, and test harnesses can be used to assist testing a module in isolation.
The purpose of integration testing is to verify functional, performance, and reliability requirements placed on major design items. These "design items", i.e., assemblages (or groups of units), are exercised through their interfaces using black box testing, success and error cases being simulated via appropriate parameters and data inputs.
While unit testing is about testing individual methods and classes and using stubs and mocks to isolate test cases from the surroundings and from each other (and frequently used in a white box approach), integration testing is a black box approach with a focus on input data. The Wikipedia article has a structural perspective on integration testing, but I think it is important to add the perspective of state as well and how this requires tests to be careful about the order of actions against the system under test.
The QS Approach
While QS uses the same notions as other test frameworks such as test classes, test methods, setup/teardown, and asserts in the code, it differs fundamentally from unit testing frameworks in other areas:
- Test methods may take any number of parameters, but unlike data driven extensions to unit frameworks, it doesn't use data sources to feed parameter values.
- Test methods can emit test data back to QS.
- Test data must be classified by one or more classification properties (classification properties have discrete types, in practice, either Booleans or enums).
- A test method is no longer the fundamental unit of a test, but must be coupled with an expression over its parameters. This expression defines one or more test conditions, which roughly amount to the preconditions that must be satisfied by the parameters of the test method. This makes the generated "test conditions" the fundamental units of the test.
- QS takes an active part in managing test data (parameters and output), both by storing output, and figuring out with which test conditions it can be used, but also, if a parameter value is not available for a test condition that must be run, by working its way backwards to figure out which test conditions it must execute to get the necessary test data.
The management and flow of test data is very powerful, but I will leave that for the next article and move on with a simple example illustrating classifications, expressions, and conditions, and conclude it with a performance measurement.
Testing the Modulus Operator
I decided to start out with something simple, and settled on the modulus operator '%' applied to the built-in types in .NET. For that, we need some numbers while QS insists on classifications, so we need to provide some (equivalence) partitioning of the range of numbers available for the different types. I settled on the following:
- Zero
- One
- A small prime (13)
MaxValue (e.g., short.MaxValue, int.MaxValue, etc.) - The largest prime smaller than
MaxValue - Positive and negative variants of the above
I'm sure this classification is debatable: I do not include MinValue, two might also be special, and for the integral types larger than 32 bit, a full test on a 32 bit system should at least also consider the boundaries around 32 and 64 bits. That said, the purpose of this test is not to find defects in .NET, but to illustrate the approach, and the choice above simplify things quite a lot.
How do we represent this for QS to understand it? We simply create an enum with the classification above, and a class with two properties, one for the classification and one of the sign (a Boolean):
enum MagnitudeEnum { Zero, One, SmallPrime, LargePrime, Max}
public class MInteger
{
public MagnitudeEnum Magnitude { get; set; }
public bool Positive { get; set; }
}
I named the class MInteger because QS works with a concept called a "meta-model", and the convention is to name meta-model classes with a capital M first. MInteger is a (very simple) meta-model for integral types, because it is a statement about the general nature of a value, but not about the specific value. QS has powerful support for meta-models, but again, more on that in a later article.
The next challenge we are facing is how to turn MInteger into a value, and how to get MInteger objects inside the QS machinery so that they can be passed as parameters to the test methods we are going to write.
I solved the first part by adding properties to MInteger, e.g., AsByte, AsShort, AsInt etc. The properties inspect the magnitude and the sign of MInteger to generate the value on the fly. I could have used conversions instead, but I want to be very explicit about how I want my values, and I don't want any surprises from implicit conversions.
The next part was easy: QS supports an attribute named SettableAttribute, and when this attribute is applied to a class, QS will check that the class has a default constructor and setters on the appropriate properties. When an instance of the class is needed, QS will create it using the default constructor and set the properties to the desired values. The resulting code for MInteger looks like this:
[Settable, Serializable]
public class MInteger
{
public MagnitudeEnum Magnitude { get; set; }
public bool Positive { get; set; }
public byte AsByte { get { ... } }
public byte AsShort { get { ... } }
public byte AsUShort { get { ... } }
public byte AsInt { get { ... } }
public byte AsUInt { get { ... } }
public byte AsLong { get { ... } }
public byte AsULong { get { ... } }
}
I made the class serializable as well. This is for the benefit of QS, and enables it to do full tracing with copies of all parameter values during execution, which enables rerun and eases debugging. QS also supports the ICloneable interface for faster or more advanced cloning, but making the class serializable is by far the easiest, and I don't need anything fast or advanced here.
Scope Creep - Measuring Performance
QS has a built-in high precision performance timer that times every execution of a test condition. I got curious about the performance characteristics of the different types, so I decided to prepare my tests for a performance test while I was at it. This amounts to feeding in an extra parameter controlling the number of iterations in a for-loop, and making sure that the timed region is placed tightly around what I want to measure.
With this in place, here is the code for testing modulus on the byte type:
[TestClass]
public class ModTests
{
[Settable, Serializable]
public class IterationControl
{
public enum IterationEnum { Once = 1, K = 1000, K50 = 50000 }
public IterationEnum Iterations { get; set; }
}
[TestMethod]
public static void ModByte(MInteger a, MInteger b, IterationControl ic)
{
byte va = a.AsByte;
byte vb = b.AsByte;
try
{
int c = 0;
int n = (int)ic.Iterations;
TestContext.Current.Timer.Start();
for (int i = 0; i != n; ++i)
{
c = va % vb;
}
TestContext.Current.Timer.Stop();
if (a.Magnitude == b.Magnitude ||
a.Magnitude == MagnitudeEnum.Zero ||
b.Magnitude == MagnitudeEnum.One)
{
Assert.AreEqual(0, c, "{0} % {1} = {2}, expected 0", va, vb, c);
}
else
{
Assert.IsTrue(c > 0, "{0} % {1} = {2}, expected > 0", va, vb, c);
}
}
catch (DivideByZeroException)
{
Assert.AreEqual(MagnitudeEnum.Zero, b.Magnitude,
"Got unexpected divide by zero exception");
}
}
}
Remarks
QS provides a thread-local test context whenever it calls a test method, and the performance timer can be controlled through that. I simply restart this timer before the loop, and stop it afterwards, to get the most precise timing.
Another thing that is different from unit tests and data driven tests is, the assertions depend on the parameters. In some cases like above, it complicates the validation part of the test method while, as odd as it may seem, it can actually simplify validation in integration scenarios.
Exceptions are always considered a fault with QS, and there is no ExpectedExceptionAttribute or similar to signal expected exceptions. It makes sense because validations depend on parameters, and as you see, I have to make the assertion in the catch block depending on the magnitude of b.
Finally, I have decided not to validate the actual value of the remainder except whether it's positive, negative, or zero. The reason for this shortcut is that, to validate the modulus, I would either need to find some mathematical relationship that I could be sure did not involve the same implementation that the modulus itself was using, or I would have to come up with an independent implementation of the modulus. In the end, I decided to trust .NET to do its arithmetic right. ;-)
Expressing Test Conditions
Having set up parameters and a test case, we are ready to get it working with QS. I'll skip the practicalities of setting up a project against the compiled assembly, and jump straight to the expression that generates conditions for my ModByte test:
a.(Positive.{True} * Magnitude.{*})
* b.(Positive.{True} * Magnitude.{*})
* ic.Iterations.{Once}
Which reads: For parameter a, set Positive to true, and try all available values for Magnitude, and for each choice of a, set b.Positive to true, and try all magnitudes for b. For all these combinations, consider only the value Once for ic.Iterations.
This expands to the following list of preconditions:
a.[Positive, Magnitude.LargePrime], b.[Positive, Magnitude.LargePrime],
ic.[Iterations.Once]
a.[Positive, Magnitude.LargePrime], b.[Positive, Magnitude.Max], ic.[Iterations.Once]
a.[Positive, Magnitude.LargePrime], b.[Positive, Magnitude.One], ic.[Iterations.Once]
a.[Positive, Magnitude.LargePrime], b.[Positive, Magnitude.SmallPrime],
ic.[Iterations.Once]
a.[Positive, Magnitude.LargePrime], b.[Positive, Magnitude.Zero], ic.[Iterations.Once]
a.[Positive, Magnitude.Max], b.[Positive, Magnitude.LargePrime], ic.[Iterations.Once]
a.[Positive, Magnitude.Max], b.[Positive, Magnitude.Max], ic.[Iterations.Once]
a.[Positive, Magnitude.Max], b.[Positive, Magnitude.One], ic.[Iterations.Once]
a.[Positive, Magnitude.Max], b.[Positive, Magnitude.SmallPrime], ic.[Iterations.Once]
a.[Positive, Magnitude.Max], b.[Positive, Magnitude.Zero], ic.[Iterations.Once]
a.[Positive, Magnitude.One], b.[Positive, Magnitude.LargePrime], ic.[Iterations.Once]
a.[Positive, Magnitude.One], b.[Positive, Magnitude.Max], ic.[Iterations.Once]
a.[Positive, Magnitude.One], b.[Positive, Magnitude.One], ic.[Iterations.Once]
a.[Positive, Magnitude.One], b.[Positive, Magnitude.SmallPrime], ic.[Iterations.Once]
a.[Positive, Magnitude.One], b.[Positive, Magnitude.Zero], ic.[Iterations.Once]
a.[Positive, Magnitude.SmallPrime], b.[Positive, Magnitude.LargePrime],
ic.[Iterations.Once]
a.[Positive, Magnitude.SmallPrime], b.[Positive, Magnitude.Max], ic.[Iterations.Once]
a.[Positive, Magnitude.SmallPrime], b.[Positive, Magnitude.One], ic.[Iterations.Once]
a.[Positive, Magnitude.SmallPrime], b.[Positive, Magnitude.SmallPrime],
ic.[Iterations.Once]
a.[Positive, Magnitude.SmallPrime], b.[Positive, Magnitude.Zero], ic.[Iterations.Once]
a.[Positive, Magnitude.Zero], b.[Positive, Magnitude.LargePrime], ic.[Iterations.Once]
a.[Positive, Magnitude.Zero], b.[Positive, Magnitude.Max], ic.[Iterations.Once]
a.[Positive, Magnitude.Zero], b.[Positive, Magnitude.One], ic.[Iterations.Once]
a.[Positive, Magnitude.Zero], b.[Positive, Magnitude.Zero], ic.[Iterations.Once]
In the project, I have made similar expressions for all built-in types (byte, short, ushort, int, uint, long, ulong, float, double, and decimal) and organized the resulting conditions into test sets for functional test, performance tests with 1000 iterations, and performance tests with 50,000 iterations.
The expression for the functional test of signed types looks like this:
a.(Positive.{*} * Magnitude.{*} - [!Positive, Magnitude.Zero])
* b.(Positive.{*} * Magnitude.{*} - [!Positive, Magnitude.Zero])
* ic.Iterations.{Once}
(The trick here is to prune the resulting tests of "negative zeroes" which would be duplicates of the "positive zeroes".)
The expression for a performance test of signed types looks like this:
a.(Positive.{*} * Magnitude.{*} - [!Positive, Magnitude.Zero])
* b.(Positive.{*} * Magnitude.{!Zero})
* ic.Iterations.{K}
It's similar to the one for signed types, except that zeroes are excluded from the denominator and the iteration count is different.
Performance Test of Modulus
Now, the code is prepared with a loop and a parameter to control the iteration count, and the QS project has been set up with separate test sets for functional tests, performance test iterating the loop 1000 times, and another set iterating the loop 50,000 times.
Why did I choose these iteration counts? First, the loop must be long enough to be measured with reasonable precisions. QS uses the high-resolution performance counter in Windows, and that should give a precision well below one microsecond when accounting for the time it takes to do the necessary calls and calculate results. To be on the safe side, the loop should not take shorter than one microsecond. The next question is how long should each measurement takes at most? To answer that, we must consider context switching and the size of the allocated time slices. If the loop runs longer than a time slice, context switches will affect all samples and shift the entire distribution of timings towards bigger values, but if the loop runs faster than a time slice, some loops will complete without encountering a context switch, and those context switches that inevitably will be encountered will show as variance instead. Microsoft states that the size of the time slice depends on the OS and processor, so there is no definitive answer, but these things usually work on the millisecond scale, so I'll assume that the loop should not run longer than 1 millisecond to get reliable data.
It turns out that 1000 iterations of the fastest operation takes about 5us on my system, which leaves room if someone comes along with a faster system. In the other end, 50,000 of these iterations take 150us which is well below the 1ms barrier.
But why should we at all consider larger iteration counts? If we are going to do a multi-threaded test, we should stay below the capacity of the test runner. QS can do about 50,000 tests/second on my system (dual-core 32 bit system) using two threads, and if we stick to 1000 iterations for the multi-threaded test (which with two threads and two cores yield up to 40,000 tests/second), QS itself will spend a significant amount of processor time and render results useless.
With this in mind, we can start doing some measurements: For the first test, I chose the test set "Performance test (K1)" containing 343 different tests across all data types. This test set does not involve exceptions (DivideByZero). I set the execution to randomized, the stop criterion to 9 seconds, disabled the throttle, and set the thread count to 1. Then it was just a matter of pressing the Run button a couple of times to get significant statistics.
Note: The free version of QS activates the throttle at a rate of 10 tests / second after 10 seconds, so I did multiple runs of 9 seconds instead. If you run this yourself, please remember to clear the history before starting a performance test, otherwise old recordings will become part of the final result.
When done, I got this report:
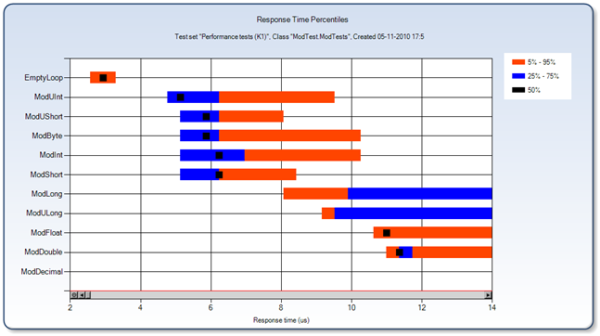
The first thing to note is that all statistics in QS are based on percentiles, and not average / variance. From a statistical point of view, that makes sense because in general, we cannot expect any particular distribution of performance timings, so we cannot reliably interpret the average and variance.
A closer inspection of the graph shows that EmptyLoop runs at 2,57us, and ModUint runs at 4.77us (lowest percentile). With an iteration count of 1000, that gives a timing of 2.2ns for a modulus operation on the uint type while byte, short, ushort, and int have best-case execution times of 2.56ns.
Is that the whole truth? Not quite! The graph shows considerable variance on the execution times, and if we zoom in on the individual test conditions, a different picture appears:

It turns out that the best execution times are obtained when the denominator is 1 and the numerator is different from 1. From there on, it gets slower until the numerator is either a large prime or uint.MaxValue, and the denominator is a small prime. In that case, the best-case execution time has increased to 4.8ns. There is still variance in the results, but this time, the variance occurs over multiple measurements with identical operands, so I will attribute that to "noise" (context switching and cache effects).
Surprised? Well, I was. I knew that the execution time of software algorithms for arithmetic functions depend on the operands (usually number and position of set bits in result), but I didn't realize the effect was so profound for how it is implemented in silicon.
To conclude this section, let's see the timings across all types, this time sorted by the median:

As before, the fastest type is uint, closely followed by byte, short, ushort, and int. On my 32-bit system, floats and doubles perform equal, while the 64 bit types long and ulong are almost an order of magnitude slower than the 32 bit types. The decimal type is in a league of its own, and based on this and other experiences, something I won't use (on a 32 bit box at least) unless I must.
Do the Cores Share Arithmetic?
To answer this question, I simply ran the tests with 50,000 iterations in one and two threads. First, one thread, with results sorted by median:

The result for two threads is very similar:

Overall, the two graphs look pretty much the same on the 5% and 95% percentiles, but the median for long and ulong move around. This turns out to be an artifact of the way I ran the test; I selected randomized execution, which means that conditions are selected at random during execution. This has the effect that during a run, some conditions will be executed more times than other conditions, and since the execution times for a type depends on the condition (i.e., the corresponding parameter values), it affects the distribution of response times. The solution is, of course, to look at the individual conditions instead.
I decided to look closer into the fastest and the slowest variants of modulus on the ulong type and view it on the trend chart. The first measurement is with one thread, and the second measurement is with two threads, and statistics is based on 2x66 measurements on the first chart, and 2x63 measurements on the second chart.


In the first chart, variance is reduced when moving from one to two threads, but since we are dealing with a relatively small sample of 66 measurements and a low chance of a sample encountering context switches (due to the low execution time), the lower variance is probably because the second test encountered fewer context switches than the first test. On the 50% and 75% percentiles, the execution time is unchanged between one and two threads, which indicates that the two cores do not share resources.
The second chart shows increased variance when moving from one thread to two threads, and this trend is consistent for all the long running conditions against the long type. Because of the longer execution time, the chance of experiencing context switches increases, so the increased variance is expected. Overall, the increasing trend is too small to suggest resource sharing between the two cores.
To conclude on the above, the measurements confirm that the two cores work independently, and do not share resources to compute the modulus.
Using the Code
The attached zip archive contains a VS 2008 project and a project file (.qgproj) for QS. There is not much to say about the VS project. The code is pretty straightforward, and follows the description above. One remark though: I had to copy-paste the test methods to make one for each of the types. In general, this is bad style - also in a test - but I could not work my way around it. Any suggestions are more than welcome.
To run the QS project, you need to download and install Quality Gate One Studio (QS), then you can simply double-click on the .qgproj files to open the QS project. You will need to check the documentation on how to use the tool.
Points of Interest
How did QS affect the ability to do the tests I set out to do?
First, because QS insists on classifying input data, I was guided (read forced) to consider my test data at a higher level by having to choose an equivalence partitioning of the test data. While my choice is clearly debatable, it gave me a set of clear cut test conditions that could be monitored individually. If I was only interested in a functional test, I could have achieved the same result with a list of predefined values and a couple of nested loops. I haven't actually tried it, but my feeling is that for this test, I would end up with about the same amount of code, but it would be very different than the code I had to write for QS.
The performance side of the test was easy to do with QS. While I still had to give some thoughts to my setup, especially how much iteration to use in the different situations, it gave me timings, iterations, threading, statistics, and graphs for free. Because the free version of QS activates the throttle after 10 seconds, I decided to run the performance tests for 9 seconds, which forced me to use the randomized execution mode. While the randomized mode has its application in a different area (scenarios), it is not ideal for the kind of low-level timing experiments I did here. I could have used the sequential execution mode instead, which would be better suited for my experiments, but it would require me to reset the throttle every 10 seconds. So let's face it, I was lazy on the execution side, and had to work harder on the analysis of the 2-core results instead.
Regarding the timing results, the conclusion is that (on a 32 bit system), uint and int are the types of choice when it comes to performance. Smaller types like byte or short have a small disadvantage because the type is expanded to 32 bits before doing arithmetic, the timing result confirms this. float and double perform equal, and generally both better and with lower variance on the timing than the long type, which is roughly a factor 10 slower than int. decimal in turn is roughly a factor 10 slower than long, which suggests that the execution time increases by a factor 10 when the size of the type doubles (int is 32 bit, long is 64 bit, and decimal is 128 bit). Whether the same holds for other operations than modulus or on other platforms has not been tested.
In the next article, I will look into the data management / data flow capabilities of QS and how that can be used when moving into integration testing. Although this may change, my current plan is to use a mock-up email server to illustrate how QS deals with data flow and time dependencies. Other suggestions are welcome.
History
- 6 Nov. 2010: First version
I started programming as a kid and went through basic, C and assembler. I got a MSc.CS from University of Aarhus in 1998 and have maintained an interest for computer science ever since, that I enjoy applying to the problems I come across. I have worked in different roles as a programmer, architect, project manager and consulting in many different areas including databases, cryptography, server architecture and distributed systems. I am currently focussing on the testing done during development and seek to improve this through a combination of approach, skill and technology.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 






