Contents
The idea for this article was born 2004 when I was working on my bachelor thesis, which included the implementation of a simulation and test environment for a flow control algorithm. For various reasons, I chose to implement it as a managed application developed with C#. The only time I regretted this choice was when I started implementing the simulation of data traffic, which requires distributed random variables. Unfortunately, I couldn't find any free-available managed implementations of random number distributions in either the .NET Framework Class Library or any other resource. So, I implemented the needed random number distributions myself. Since then, I've had the idea to create a class library on the basis of these few implementations and publish it here on CodeProject, but I've never really had the time to realize it. Until now.
The Random Class Library contains abstract base classes for random number generators and random number distributions, as well as various concrete classes that are derived from both. Before I start to describe these classes, I have to mention that all algorithms which generate the (distributed) random numbers aren't my intellectual work, as I'm no brilliant mathematician. Thereforee this article, as well as the source code, contain references to the respective knowledge resources.
The Generator type declares common functionality for all random number generators. This includes the one provided by the System.Random type, plus some extensions. So, the class additionally declares two overloads for the NextDouble method, a NextBoolean method and the possibility to reset the random number generator. This can be very useful when using pseudo-random number generators. The following table lists all abstract members, together with a brief description.
| Abstract Member | Description |
|---|
bool CanReset { get; } | Gets a value indicating whether the random number generator can be reset, so that it produces the same random number sequence again. |
bool Reset(); | Resets the random number generator, so that it produces the same random number sequence again.
Returns true, if the random number generator was reset; otherwise, false. |
int Next(); | Returns a nonnegative random number less than Int32.MaxValue; that is, the range of return values includes 0 but not Int32.MaxValue. |
int Next(<br />int maxValue); | Returns a nonnegative random number less than the specified maximum; that is, the range of return values includes 0 but not maxValue.
maxValue must be greater than or equal to 0. |
int Next(<br />int minValue,<br />int maxValue); | Returns a random number within the specified range; that is, the range of return values includes minValue but not maxValue.
maxValue must be greater than or equal to minValue. |
double NextDouble(); | Returns a nonnegative floating point random number less than 1.0; that is, the range of return values includes 0.0 but not 1.0. |
double NextDouble(<br />double maxValue); | Returns a nonnegative floating point random number less than the specified maximum; that is, the range of return values includes 0.0 but not maxValue.
maxValue must be greater than or equal to 0.0. |
double NextDouble(<br />double minValue,<br />double maxValue); | Returns a floating point random number within the specified range; that is, the range of return values includes minValue but not maxValue.
maxValue must be greater than or equal to minValue. The distance between minValue and maxValue must be less than or equal to Double.MaxValue. |
bool NextBoolean(); | Returns a random Boolean value. |
void NextBytes(<br />byte[] buffer); | Fills the elements of a specified array of bytes with random numbers.
Each element of the array of bytes is set to a random number greater than or equal to 0, and less than or equal to Byte.MaxValue. |
Currently, the library provides four classes derived from Generator. These are listed in the following table, together with a short description and links for further reading.
| Implementation | CanReset | Description / Links |
|---|
| ALFGenerator | true | Represents an Additive Lagged Fibonacci pseudo-random number generator with some additional Next methods.
This type is based upon the implementation in the Boost Random Number Library. It uses the modulus 232 and, by default the, "lags" 418 and 1279. This can be adjusted through the associated ShortLag and LongLag properties. Some popular pairs are presented on Wikipedia - Lagged Fibonacci generator. |
| MT19937Generator | true | Represents a Mersenne Twister pseudo-random number generator with period 219937-1 and some additional Next methods.
This type is based upon information and the implementation presented on the Mersenne Twister Home Page. |
| StandardGenerator | true | Represents a simple pseudo-random number generator.
This type internally uses an instance of the System.Random type to generate pseudo-random numbers. |
| XorShift128Generator | true | Represents a xorshift pseudo-random number generator with period 2128-1 and some additional Next methods.
This type is based upon the implementation presented in the CP article " A fast equivalent for System.Random" and the theoretical background on xorshift random number generators published by George Marsaglia in the paper "Xorshift RNGs". |
The Distribution class declares common functionality for all random number distributions. Its abstract members which have to be implemented by inheritors are some properties providing information on distribution characteristics and the NextDouble method. The following table lists all abstract members together with a brief description.
| Abstract Member | Description |
|---|
double Minimum { get; } | Gets the minimum possible value of distributed random numbers. |
double Maximum { get; } | Gets the maximum possible value of distributed random numbers. |
double Mean { get; } | Gets the mean of distributed random numbers.
If the mean can't be computed, the Double.NaN constant will be returned. |
double Median { get; } | Gets the median of distributed random numbers.
If the median can't be computed, the Double.NaN constant will be returned. |
double Variance { get; } | Gets the variance of distributed random numbers.
If the variance can't be computed, the Double.NaN constant will be returned. |
double[] Mode { get; } | Gets the mode of distributed random numbers.
If the mode can't be computed, an empty array will be returned. |
double NextDouble(); | Returns a distributed floating point random number. |
In addition to its abstract members, the Distribution type provides some implementation details common to all random number distributions. As the computation of distributed random numbers necessarily requires a random number generator, the generator field stores an instance of the Generator class. This instance is accessible to inheritors through its respective property. Furthermore, two protected constructors are defined: one takes a user-defined Generator object and the other is a standard constructor that applies an instance of the StandardGenerator type. The Distribution type also offers the same reset functionality as the Generator class. In fact, it simply forwards the results of the stored Generator instance, as a random number distribution can only be reset if its underlying random number generator is resettable.
public abstract class Distribution
{
protected Generator Generator
{
get { return this.generator; }
set { this.generator = value; }
}
private Generator generator;
protected Distribution() : this(new StandardGenerator())
{
}
protected Distribution(Generator generator)
{
if (generator == null)
{
string message = string.Format(null,
ExceptionMessages.ArgumentNull, "generator");
throw new ArgumentNullException("generator", message);
}
this.generator = generator;
}
public bool CanReset
{
get { return this.generator.CanReset; }
}
public virtual bool Reset()
{
return this.generator.Reset();
}
...
}
The Random Class Library currently provides Distribution inheritors for various continuous and discrete distributions. They are listed in the following tables, together with a short description, links for further reading and information on the range and specific distribution parameters.
Discrete Distributions
(All of them additionally implement a Next method, which returns a distributed random number, i.e. 32-bit signed integer.)| Implementation | Parameter / Range | Description |
|---|
| BernoulliDistribution |
| Provides generation of Bernoulli distributed random numbers.
This type is based upon information presented on Wikipedia - Bernoulli distribution. |
| BinomialDistribution | 0 ≤ α ≤ 1
β ∈ {0,1,...} | | X ∈ {0,1,...,β} |
| Provides generation of binomial distributed random numbers.
This type is based upon information presented on Wikipedia - Binomial distribution. |
| DiscreteUniformDistribution | α ∈ {...,β-1,β}
β ∈ {α,α+1,...} | | X ∈ {α,α+1,...,β-1,β} |
| Provides generation of discrete uniformly distributed random numbers.
This type is based upon information presented on Wikipedia - Uniform distribution (discrete). |
| GeometricDistribution |
| Provides generation of geometric distributed random numbers.
This type is based upon information presented on Wikipedia - Geometric distribution and the implementation in the Communication Networks Class Library. |
| PoissonDistribution |
| Provides generation of Poisson distributed random numbers.
This type is based upon information presented on Wikipedia - Poisson distribution and the implementation in the Communication Networks Class Library. |
Besides the inherited members, all classes derived from Distribution share some more similarities. Firstly, all distributions offer two constructors: one that takes a user-defined Generator object as an underlying random number generator and another as a standard constructor that uses an instance of StandardGenerator type for this purpose.
Secondly, each distribution provides methods that allow you to determine whether a value is valid for one of its specific parameters and thereforee can be assigned through the belonging property. These methods follow the naming scheme "IsValid{parameter}" and, to be consistent, are also available for parameters whose range of values isn't restricted.
Also, the classes derived from Distribution make use of helper variables to speed up the random number generation, if possible. These helpers store intermediate results that only depend on distribution parameters and therefore don't need to be recalculated in successive executions of NextDouble. The computation of the helper variables is encapsulated inside the UpdateHelperVariables method, which gets called during construction and whenever a distribution parameter involved in the helper's calculation changes. The following code snippet is taken from the PoissonDistribution type and should illustrate the preceding explanations.
public class PoissonDistribution : Distribution
{
public double lambda;
private double helper1;
public double Lambda
{
get { return this.lambda; }
set
{
if (this.IsValidLambda(value))
{
this.lambda = value;
this.UpdateHelpers();
}
}
}
public PoissonDistribution() : this(new StandardGenerator())
{
}
public PoissonDistribution(Generator generator) : base(generator)
{
this.lambda = 1.0;
this.UpdateHelpers();
}
public bool IsValidLambda(double value)
{
return value > 0.0;
}
private void UpdateHelpers()
{
this.helper1 = Math.Exp(-1.0 * this.lambda);
}
public double NextDouble()
{
double count = 0;
for (double product =
this.generator.NextDouble(); product >= this.helper1;
product *= this.generator.NextDouble())
{
count++;
}
return count;
}
...
| 1.4 |
- Changed the
Distribution.Reset method to be virtual, so it can be overridden in derived classes - Overridden the
Reset method in the NormalDistribution: The override discards an already computed random number to be returned next -- the underlying generation algorithm always computes two random numbers at a time -- so the distribution is always properly reset - Overridden the
Reset method in the BetaDistribution, BetaPrimeDistribution, ChiDistribution, ChiSquareDistribution, FisherSnedecorDistribution, LogNormalDistribution, RayleighDistribution and StudentsTDistribution: The override explicitly resets the respective underlying distribution(s), which in most cases is the NormalDistribution, so the listed distributions are always properly reset
|
| 1.3 |
- Fixed bug in
NormalDistribution: Changes to the parameters μ and σ now discard an already computed random number to be returned next -- the underlying generation algorithm always computes two random numbers at a time -- so in any case changes to the parameters reflect in generated random number beginning with the first one
|
| 1.2 |
- Changed the access modifier of field
Distribution.generator from protected to private and made it accessible through the new protected property Distribution.Generator
Adapted all inheritors of Distribution to the above change
Follow the link for further explanation: Visual Studio Team System - Do not declare visible instance fields - Moved reinitialization code of
ALFGenerator, MT19937Generator, StandardGenerator and XorShift128Generator types from their virtual Reset methods to new private ResetGenerator methods, so it can be safely called from their constructors (and Reset too)
Follow the link for further explanation: Visual Studio Team System - Do not call overridable methods in constructors - Adjusted
NextBytes method of ALFGenerator, MT19937Generator and XorShiftGenerator type so they check whether the passed buffer is a null reference and throw an ArgumentNullException if needed - All exceptions are instantiated with localized messages; currently available are English, German, Spanish and French translations
|
| 1.1 |
- Added Bernoulli, Beta-prime, Binomial, Chi, Chi-square, Erlang, Fisher-Snedecor, Fisher-Tippett, Laplace, Rayleigh, Student's t and Weibull random distribution
- Added Additive Lagged Fibonacci pseudo-random number generator
- Renamed property for the parameter μ of
LognormalDistribution and NormalDistribution from My to Mu to consistently use English names - Fixed bug in
PowerDistribution: Changes to parameter α now reflect in generated random numbers - Adjusted
ExponentialDistribution.NextDouble so that Math.Log(0.0) is avoided - Improved performance of
MT19937Generator.Next and XorShift128Generator.Next with specified range for range > Int32.MaxValue
|
| 1.0 |
|
Random Class Library is free software. You can redistribute it and/or modify it under the terms of the GNU Lesser General Public License as published by the Free Software Foundation, either version 2.1 of the License, or (at your option) any later version. This library is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY, without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU Lesser General Public License for more details. You should have received a copy of the GNU Lesser General Public License along with this library. If not, write to the Free Software Foundation, Inc., 51 Franklin Street, Fifth Floor, Boston, MA 02110-1301 USA.
I'd begun developing the RandomTester application when I implemented the first random number distributions for my bachelor thesis. At the time, its only purpose was to visualize the distribution of generated random numbers and the effects of the specific distribution parameters upon it. During the work on the Random Class Library, I refined this visualization and added performance tests for random number generators and distributions.
The RandomTester application allows you to test and compare random number generators with respect to their performance. The following picture shows the user interface of this test after running it.
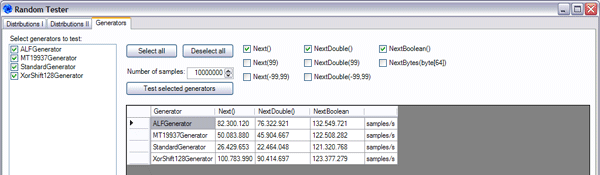
All classes derived from Generator are listed at the left edge. They can be selected/deselected either one-by-one through clicking them on the respective list entry or all at once by using the "Select all" or "Deselect all" buttons. Beneath those buttons you can specify how many samples have to be generated by each generator to benchmark their performance. Finally, one has to choose which Next methods -- declared by the Generator type and implemented in the derived classes -- should be tested. The performance of random number generators is measured in calls per second. The results are displayed in a datagrid that contains a row for each random number generator and a column for each tested Next method.
Random number distributions can be tested in two ways. Firstly, a performance test is available that is similar to the one provided for the random number generators. Secondly, the distribution of generated random numbers and the effects of the specific distribution parameters upon it can be visualized. The user interface of those tests is shown by the below image.

As mentioned, the performance test is similar to the random number generator benchmark. At the left edge, all classes derived from Distribution are listed and can be selected/deselected either one by one through clicking on the respective list entry or all at once by using the "Select all" or "Deselect all" buttons. Furthermore the number of samples each distribution has to generate during the benchmark can be specified, as well as an underlying random number generator. The latter adjustment offers to use a class derived from Generator or the distribution default. In case an inheritor of Generator gets selected, the tested distributions are instantiated using their constructor when taking such an object. Otherwise, the standard constructor is used. The performance of the selected random number distributions is expressed as the time it takes to generate the specified number of samples. The results are shown in ascending order inside the textbox.
In contrast to both performance tests, the main focus of the visualization test isn't performance but rather the testing of a single random number distribution. Therefore it employs a ZedGraphControl to show a histogram of the distribution of generated random numbers, i.e. how often distinct values occur or, more precisely, how likely it is for them to occur (probability density function).
In case of discrete distributions, this can be done easily by counting the occurrences of discrete values and dividing by the overall number of generated samples. Unfortunately, most random number distributions are continuous and have a quite large range. Thus, the probability of a given value being generated more than once is fairly low, even if many numbers are generated. That's why the visualization test divides the domain of generated samples into a specified number of sections and then shows how likely it is for the values inside these sections to occur. Such a histogram is also used for discrete random number distributions, since it provides the same results as long as the number of sections is equal to or greater than the number of discrete values. In this case, the complicated distinction between distribution types becomes redundant.
At the top left corner, a dropdown list lets you select the distribution to be visualized from all classes derived from Distribution. Beneath that list, a groupbox displays the current characteristics of the selected distribution. A second groupbox allows you to adjust the specific parameters. Depending on the selected distribution, the change of a parameter also causes one or more of its characteristics to change. The final adjustment directly related to the distribution is the selection of an underlying random number generator that allows you to choose either the distribution default or a class derived from Generator.
Any further settings are related to the visualization of the random number distribution. You can specify how many samples and sections are used to create the histogram, whether the histogram curves should be smoothed and whether specific bounds are used, i.e. any generated random number lying outside will be ignored.
As shown by the above image, multiple histograms can be displayed at the same time. This allows you to examine the effects of the parameters on the distribution of random numbers or even compare different distributions. Each newly generated histogram is drawn as a separate curve. The name and parameter values of the tested distribution are added to the legend. In addition to the histogram, the bottom left textbox shows how much time was needed to generate the random numbers, as well as their minimum, maximum, mean and variance.
| 1.2 |
- Adjusted distribution visualization so that the last interval of histograms is displayed correctly
Until now, the histogram graphs consisted of points representing the minimum bounds of histogram intervals, so the last interval wasn't really drawn. Therefore graphs now contain an additional point for the maximum bound of the last interval which, of course, has the same y-value as the corresponding minimum bound.
|
| 1.1 |
- Display unit "samples/s" in generator test
- Use byte[64] for testing
Generator.NextBytes method so the test is less time consuming
|
| 1.0 |
|
RandomTester is free software. You can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 2 of the License, or any later version. This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY, without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details. You should receive a copy of the GNU General Public License along with this program; if not, write to the Free Software Foundation, Inc., 59 Temple Place, Suite 330, Boston, MA 02111-1307 USA.
- Wikipedia - Random number generator
- Mersenne Twister Home Page
- A fast equivalent for System.Random
- Paper "Xorshift RNGs" by George Marsaglia
- Wikipedia - Probability distribution
- MathWorld - Statistical Distribution
- Xycoon - Statistical Distributions
- Boost Random Number Library
- Communication Networks Class Library
- A flexible charting library for .NET
Article history
- 29 May, 2007 - Article edited and posted to the main CodeProject.com article base
This member has not yet provided a Biography. Assume it's interesting and varied, and probably something to do with programming.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 





