Introduction
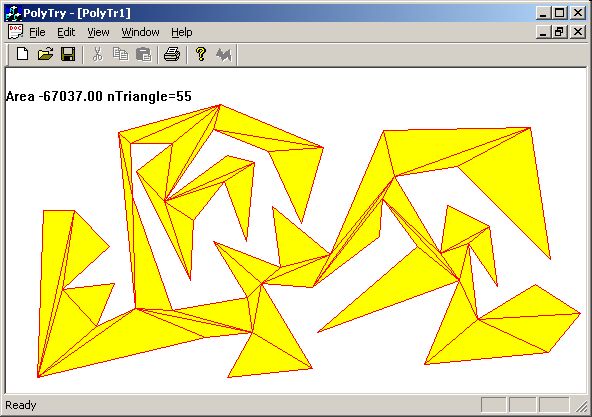
A simple alternative to OpenGL polygon tesselation callback. You can focus on file triangle.h that contain the class to evaluate convexity of polygon and tesselate the polygon. No extra points are inserted. You can work only with planar polygon also in 3D.
Every suggestion in order to speed up the class and create better tesselation ('better' triangles) is appreciated.
History
- 6th February, 2002: Initial post
This member has not yet provided a Biography. Assume it's interesting and varied, and probably something to do with programming.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin