Introduction
Continued fractions are of great importance in many aspects, as they have many implementations for real problems where you want to describe something with an approximate fraction, or you simply want to replace a decimal or double number with a fraction.
Background
As always in mathematics the history of continued fractions are quite complicated. The earliest traces of continued fractions appear as far back as 306 b.c. Other records have been found that show that the Indian mathematician Aryabhata used a continued fraction to solve a linear equation.
In the western hemisphere it did not appear until the 17th century, when William Brouncker and John Wallis started to formulate some form of continued fractions. The Dutch mathematician and astronomer, Christiaan Huygens made the �first practical application of the theory in 1687, and wrote a paper explaining how to use convergents to �achive the best rational approximations for gear ratios. These approximations enabled him to pick the gears with the best numbers of teeth as he was going to build a mechanical planetarium.
Representation and calculations of continued fractions
How to write a continued fraction anyway, well let's take the simple quadratic equation:
x^2 - bx -1 = 0
Move things over and divide by X and you can rewrite it like this:
x = b + 1/x
We realize that we have a formula for X on the left, and we have an X on the right side. We now substitute the X on the right side with the formula on the right. Sounds complicated, but here is the result with one substitution:
x = b + 1/(b + 1/x)
We can do this an infinite number of times and get a continued fraction. This is an interesting formula if we plug in b = 1 we would get the golden ration. (to get this number you simply type in (sqrt(5)-1)/2 in the program submitted).
In the general representation of a continued fraction is given below, where x is a number (irrational or rational) and the coefficients a0, a1, and so on are all positive integers.

The continued fraction is quite complicated to write in this way, so they are usually represented as a series of the coefficients as given below:

Finite numbers would have a finite set of fractions, while irrational number (sqrt(2)) could be given a rational approximate representation if you adruptly stop it at one of the coefficients. This is called the n'th convergent of the continued fraction.
To calculate the numbers an you should simply do this:
a0 = Math.Floor(some decimal number)
we must also store the rest of the number in the temporary variable b:
b = some decimal number - Math.Floor(some decimal number)
a1 = 1/(b)
If we continue this, as shown in the code below, we would get all the expansions we desire:
Private Function GetSeriesExpantion(ByVal input As Decimal, ByVal NrFraction As Integer) As Integer
Dim intput As Decimal = input
Dim temp_dec As Integer
For i As Integer = 0 To NrFraction
temp_dec = CInt(Math.Floor(intput))
intput = intput - Math.Floor(intput)
If Not intput = 0 Then
intput = 1 / intput
Else
intput = 0
End If
Next
Return temp_dec
End Function
To get the resulting n'th convergent fraction I have designed an own fraction struct that can add a whole number to a fraction, and the result would be given below the an series in the program.
Continued fractions in action
Why go to all of this trouble? Well as it turns out continued fractions produces a much better
approximation then the 10 digit system (for instance 314/100 in the case of Pi). You should also notice that the fraction approximation is better, the sooner you get a large number in the An series. As a direct result of this, the worst case scenario would be an expansion were all the numbers (in the An series) is 1.
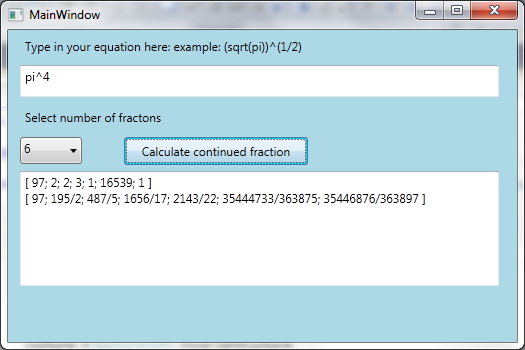
An example were a series can be terminated at a hugh number is shown in the first program demo picture. The result was discovered by Ramanujan, who was an extraordenary natural talent in mathematics. He studied continued fractions and found, among other things, an approximate formula for pi written like this:
pi = (2143/22)^(1/4)
This is an accurate to the 8 digit after the decimal sign, and that really should be good enough for any practical use! To see why this approximation works so well, you should take a note of the example picture in the beginning of the article. It shows the continued expasion of the number pi^4 and as you can see the number a5 is over 16000, and if we cut the continued series expansion we would get the number in Ramanujan's approximate formula for pi.
To summarize the uses of continued fractions:
- The scale models are can be created with small errors using the convergent
- They convert rather quickly in comparison to other techniques.
- We've seen that they have many computationally desirable properties
- They represent all real numbers accurately
- They yield good approximations when truncated
- They're easy to compare
- They have no weird biases toward the number 10
Why don't we see them used more often? (I've seen other articles on the codeproject site that convert a decimal number to a fraction; this should also be done by using the continued fractions.)
History
The article with all the explanations is based heavily on the reference given below, and my contribution is quite small, as I only made the program that gives you the possibility to calculate them easily.
The evaluator is simply the one I made previously for complex numbers, as I do not have the permission to publish the code with double taken from "Programming Microsoft Visual Basic .NET" (2003) - Francesco Balena (pages 505 - 509.). The evaluator should be replased with one that takes decimal numbers to get more accurate results.
References
There is an excellent video by Professor John Barrow on Continued Fractions available on fora.tv for free, if you like to know more be sure to check it out. Some of the material from this article is from the video by him:
http://fora.tv/2010/11/16/Gresham_Professor_John_Barrow_Continued_Fractions
And some description from Barrow's web site:
http://plus.maths.org/content/chaos-numberland-secret-life-continued-fractions
Some other websites that are useful:
http://archives.math.utk.edu/articles/atuyl/confrac/
http://en.wikipedia.org/wiki/Continued_fraction
http://www-math.mit.edu/phase2/UJM/vol1/COLLIN~1.PDF
This member has not yet provided a Biography. Assume it's interesting and varied, and probably something to do with programming.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 











