Introduction
This is a sequel to the previous article on Kalman filtering, and can be thought of as a more elaborate and more useful example. Kalman filters
do a particularly good job of adaptively removing noise from a signal with as little distortion as possible. This example is for 2D navigation using a GPS and an inexpensive accelerometer.
Suppose you wanted to mow the lawn, or have a robot drop off a letter, or navigate very accurately off road. GPS provides inaccurate position and velocities (2.5 m rms, 10 cm rms,
respectively)
and using position and velocity a 2D Kalman filter will improve things.
Using only GPS means at best the signal to noise improves by averaging (sqrt(1/n)) and at 5 to 10 Hz the accuracy degrades rapidly with course changes.
GPS also will “jump” in location as different satellites are periodically chosen to be added / removed from the solution. This jump is sometimes 10-15 meters.
The velocity from GPS (computed from Doppler) has less noise, and “jumps” less when the satellite constellation changes.
The solution is to add another data source. There are several accelerometers available that can measure the linear acceleration. Simply put, they provide
the rate of change in velocity, and after a coordinate transform, an do so in the same coordinate space as the GPS. In addition to a linear accelerometer,
an angular with a second GPS would provide the course and further refine the solution, but for this example a linear accelerometer should be sufficient for a dramatic improvement.
Relying only on the accelerometer causes a drift as noise and round off integrate.
The ideal thing about the accelerometer is the noise is small (0.002 m rms), it can be measured rapidly (1Hz – 5kHz), the errors are Gaussian (average out)
and the error sources are completely different than GPS. Because there is no connection in noise source, the accelerometer and GPS error sources tend to cancel out.
Requirements
Assuming we can get decent HW (below are very available HW specs at reasonable prices).
GPS 2.5 m rms, 10 Hz
Accelerometer 2 mm rms, 1 kHz
Operational goal:
Goal <25 cm rms for low dynamic movements
Design
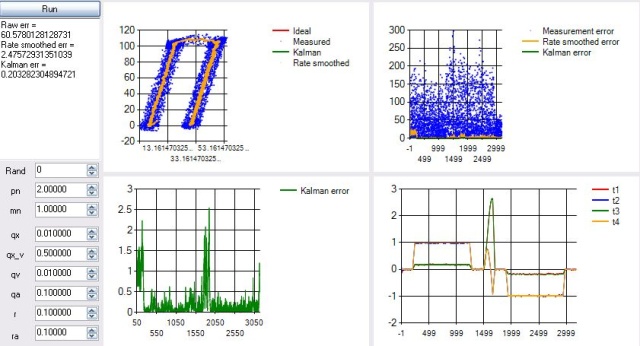
The source code could have used a 3D Kalman filter (position, velocity, acceleration) but there is no real correlation between the GPS and the acceleration.
It is simpler to use two filters and optimize each separately. One filter computes the velocity as a 2D Kalman (velocity, acceleration) such that the GPS Doppler
is smoothed / corrected by the acceleration measurements. A second filter takes the highly accurate velocity information and filters in position.
To get this to work in the horizontal plane, two filters for X (position, velocity) and two for Y (position and velocity) were used.
The test scenario is accelerating from a stop, cruising, slowing down, rotating, slow to stop, then start up and cruise back.
Conclusion
The stock coefficients provided yield good accuracy balanced with good responsiveness: once acceleration is detected it immediately helps shift the position,
the GPS slowly corrects against drift. I’m hoping to use this for a robots project in the future, and I’m hoping it helps others out there.
Phil is a Principal Software developer focusing on weird yet practical algorithms that run the gamut of embedded and desktop (PID loops, Kalman filters, FFTs, client-server SOAP bindings, ASIC design, communication protocols, game engines, robotics).
In his personal life he is a part time mad scientist, full time dad, and studies small circle jujitsu, plays guitar and piano.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 






 example acc+gyro fusion.
example acc+gyro fusion.

