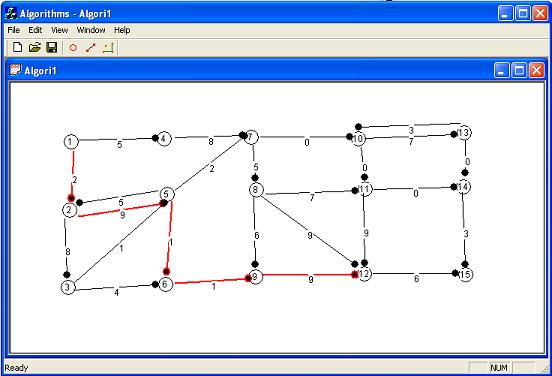
Introduction
First of all I must say that I am glad that I can help CodeProject. I tried, and used code from this site and I never took the time to send some of my code. So, the part that it is missing from this site is the Algorithms part, which is important in the programming filed. Let's get into the problem now. The Djkstra algorithm it gives you a headache from the programming point of view. In one step it finds the shortest path to every node in the graph. I will go into the graph background (basics) and then I will present the implementation of this algorithm. This example has also some advanced programming techniques and technologies. I used an ActiveX control (that it is actually the Dijkstra solver) and a container application that use the functions. Also, the lists are made using STL
How to use it
First compile the AnimAlg project and then run the Algorithms project. That's all!
Background (graph theory)
Djikstra's algorithm (named after its discover, E.W. Dijkstra) solves the problem of finding the shortest path from a point in a graph (the source) to a destination. It turns out that one can find the shortest paths from a given source to all points in a graph in the same time, hence this problem is sometimes called the single-source shortest paths problem. The somewhat unexpected result that all the paths can be found as easily as one further demonstrates the value of reading the literature on algorithms!
This problem is related to the spanning tree one. The graph representing all the paths from one vertex to all the others must be a spanning tree - it must include all vertices. There will also be no cycles as a cycle would define more than one path from the selected vertex to at least one other vertex. For a graph,
G = (V,E) where V is a set of vertices and E is a set of edges. Dijkstra's algorithm keeps two sets of vertices: S the set of vertices whose shortest paths from the source have already been determined and V-S the remaining vertices. The other data structures needed are: d array of best estimates of shortest path to each vertex pi an array of predecessors for each vertex The basic mode of operation is: Initialize d and pi, Set S to empty, While there are still vertices in V-S, Sort the vertices in V-S according to the current best estimate of their distance from the source, Add u, the closest vertex in V-S, to S, Relax all the vertices still in V-S connected to u Relaxation The relaxation process updates the costs of all the vertices, v, connected to a vertex, u, if we could improve the best estimate of the shortest path to v by including (u,v) in the path to v.
Using the code
The container application only use the ActiveX Control. First, must include the control in a Dialog or a FormView, add a variable to it and then use the following code:
void CAlgorithmsView::OnAddNode()
{
m_Dijkstra.StartAddNodes();
}
void CAlgorithmsView::OnAddEdge()
{
m_Dijkstra.StartAddEdges();
}
void CAlgorithmsView::OnShortestPath()
{
CShorthestPath dlg;
if(dlg.DoModal()==IDOK)
{
m_Dijkstra.ShortestPath(dlg.m_node1, dlg.m_node2);
}
}
I will not go too much into the code, I tried to explain there using comments.
Basically, it respects the Graph Theory explained above and the Dijkstra's pseudocode.
Graph Implementation
class CGraph
{
public:
long GetNrNodes();
CGraph();
virtual ~CGraph();
VTYPE_NODE m_nodes;
VTYPE_EDGE m_edges;
VTYPE_NODE_P d;
VTYPE_NODE_P pi;
};
class CNode
{
public:
CNode Copy();
double m_cost;
long m_NodeNr;
POINT m_p;
CNode();
virtual ~CNode();
};
class CEdge
{
public:
bool m_red;
double m_cost;
long m_secondNode;
long m_firstNode;
POINT m_secondPct;
POINT m_firstPct;
CEdge();
virtual ~CEdge();
};
The Dijkstra's Algorithm (Implementation)
STDMETHODIMP CDijkstra::ShortestPath(long node1, long node2)
{
ReleaseGraph();
InitializeSource(g, g.m_nodes[node1-1]);
VTYPE_NODE S;
VTYPE_NODE Q;
VTYPE_NODE::iterator kl;
for(kl=g.m_nodes.begin(); kl<g.m_nodes.end(); kl++)
{
CNode node = (*kl).Copy();
Q.push_back(node);
}
while(Q.size())
{
CNode nod = ExtractMin(Q);
S.push_back(nod);
VTYPE_NODE::iterator kl;
for(kl=g.m_nodes.begin(); kl<g.m_nodes.end(); kl++)
{
if(ExistEdge(nod, (*kl)))
{
bool gasit = false;
VTYPE_NODE::iterator kll;
for(kll=Q.begin(); kll<Q.end(); kll++)
{
if((*kll).m_NodeNr == (*kl).m_NodeNr)
gasit = true;
}
if(gasit)
Relax(nod, (*kl), GetEdgeVal(nod, (*kl)));
}
}
}
RefreshDone(node1, node2);
return S_OK;
}
Links
If you want to see how the algorithm works step by step see the link: http://ciips.ee.uwa.edu.au/~morris/Year2/PLDS210/dij-op.html
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 







