Contents
Introduction
When you hear the word persistence in programming, most often, you think of an application saving its data to some type of storage, such as a database, so that the data can be retrieved later when the application is run again. There is, however, another meaning for the word persistence when it is used to describe data structures, particularly those used in functional programming languages. In that context, a persistent data structure is a data structure capable of preserving the current version of itself when modified. In essence, a persistent data structure is immutable.
An example of a class that uses this type of persistence in the .NET Framework is the string class. Once a string object is created, it cannot be changed. Any operation that appears to change a string generates a new string instead. Thus, each version of a string object can be preserved. An advantage for a persistent class like the string class is that it basically gives you undo functionality built-in. As newer versions of a persistent object are created, older versions can be pushed onto a stack and popped off when you want to undo an operation. Another advantage is that because persistent data structures cannot change state, they are easier to reason about and are thread safe.
There is an overhead that comes with persistent data structures, however. Each operation that changes a persistent data structure creates a new version of that data structure. This can involve a good deal of copying to create the new version. This cost can be mitigated to a large degree by reusing as much of the internal structure of the old version in creating a new one. I will explore this idea in making two common data structures persistent: the singly linked list and the binary tree, and describe a third data structure that combines the two. I will also describe several classes I have created that are persistent versions of some of the classes in the System.Collections namespace.
top
Persistent Singly Linked Lists
The singly linked list is one of the most widely used data structures in programming. It consists of a series of nodes linked together one right after the other. Each node has a reference to the node that comes after it, and the last node in the list terminates with a null reference. To traverse a singly linked list, you begin at the head of the list and move from one node to the next until you have reached the node you are looking for or have reached the last node:
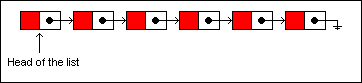
Let's insert a new item into the list. This list is not persistent, meaning that it can be changed in-place without generating a new version. After taking a look at the insertion operation on a non-persistent list, we'll look at the same operation on a persistent list.
Inserting a new item into a singly linked list involves creating a new node:

We will insert the new node at the fourth position in the list. First, we traverse the list until we've reached that position. Then the node that will precede the new node is unlinked from the next node...

...and relinked to the new node. The new node is, in turn, linked to the remaining nodes in the list:

Inserting a new item into a persistent singly linked list will not alter the existing list but create a new version with the item inserted into it. Instead of copying the entire list and then inserting the item into the copy, a better strategy is to reuse as much of the old list as possible. Since the nodes themselves are persistent, we don't have to worry about aliasing problems.
To insert a new node at the fourth position, we traverse the list as before only copying each node along the way. Each copied node is linked to the next copied node:

The last copied node is linked to the new node, and the new node is linked to the remaining nodes in the old list:

On an average, about N/2 nodes will be copied in the persistent version for insertions and deletions, where N equals the number of nodes in the list. This isn't terribly efficient but does give us some savings. One persistent data structure where this approach to singly linked list buys us a lot is the stack. Imagine the above data structure with insertions and deletions restricted to the head of the list. In this case, N nodes can be reused for pushing items onto a stack and N - 1 nodes can be reused for popping a stack.
top
Persistent Binary Trees
A binary tree is a collection of nodes in which each node contains two links, one to its left child and another to its right child. Each child is itself a node, and either or both of the child nodes can be null, meaning that a node may have zero to two children. In the binary search tree version, each node usually stores a key/value pair. The tree is searched and ordered according to its keys. The key stored at a node is always greater than the keys stored in its left descendents and always less than the keys stored in its right descendents. This makes searching for any particular key very fast.
Here is an example of a binary search tree. The keys are listed as numbers; the values have been omitted but are assumed to exist. Notice how each key as you descend to the left is less than the key of its predecessor, and vice versa as you descend to the right:

Changing the value of a particular node in a non-persistent tree involves starting at the root of the tree and searching for a particular key associated with that value, and then changing the value once the node has been found. Changing a persistent tree, on the other hand, generates a new version of the tree. We will use the same strategy in implementing a persistent binary tree as we did for the persistent singly linked list, which is to reuse as much of the data structure as possible when making a new version.
Let's change the value stored in the node with the key 7. As the search for the key leads us down the tree, we copy each node along the way. If we descend to the left, we point the previously copied node's left child to the currently copied node. The previous node's right child continues to point to nodes in the older version. If we descend to the right, we do just the opposite.
This illustrates the "spine" of the search down the tree. The red nodes are the only nodes that need to be copied in making a new version of the tree:

You can see that the majority of the nodes do not need to be copied. Assuming the binary tree is balanced, the number of nodes that need to be copied any time a write operation is performed is at most O(Log N), where Log is base 2. This is much more efficient than the persistent singly linked list.
Insertions and deletions work the same way, only steps should be taken to keep the tree in balance, such as using an AVL tree. If a binary tree becomes degenerate, we run into the same efficiency problems as we did with the singly linked list.
top
Random Access Lists
An interesting persistent data structure that combines the singly linked list with the binary tree is Chris Okasaki's random-access list. This data structure allows for random access of its items as well as adding and removing items from the beginning of the list. It is structured as a singly linked list of completely balanced binary trees. The advantage of this data structure is that it allows access, insertion, and removal of the head of the list in O(1) time as well as provides logarithmic performance in randomly accessing its items.
Here is a random-access list with 13 items:

When a node is added to the list, the first two root nodes (if they exist) are checked to see if they both have the same height. If so, the new node is made the parent of the first two nodes; the current head of the list is made the left child of the new node, and the second root node is made the right child. If the first two root nodes do not have the same height, the new node is simply placed at the beginning of the list and linked to the next tree in the list.
To remove the head of the list, the root node at the beginning of the list is removed, with its left child becoming the new head and its right child becoming the root of the second tree in the list. The new head of the list is right linked with the next root node in the list:

The algorithm for finding a node at a specific index is in two parts: in the first part, we find the tree in the list that contains the node we're looking for. In the second part, we descend into the tree to find the node itself. The following algorithm is used to find a node in the list at a specific index:
- Let I be the index of the node we're looking for. Set T to the head of the list where T will be our reference to the root node of the current tree in the list we're examining.
- If I is equal to 0, we've found the node we're looking for; terminate algorithm. Else if I is greater than or equal to the number of nodes in T, subtract the number of nodes in T from I and set T to the root of the next tree in the list and repeat step 2. Else if I is less than the number of nodes in T, go to step 3.
- Set S to the number of nodes in T divided by 2 (the fractional part of the division is ignored. For example, if the number of nodes in the current subtree is 3, S will be 1).
- If I is less than S, subtract 1 from I and set T to T's left child. Else subtract (S + 1) from I and set T to T's right child.
- If I is equal to 0, we've found the node we're looking for; terminate algorithm. Else go to step 3.
This illustrates using the algorithm to find the 10th item in the list:

Keep in mind that all operations that change a random-access list do not change the existing list but rather generate a new version representing the change. As much of the old list is reused in creating a new version.
top
Immutable Collections
Included with this article are a number of persistent collection classes I have created. These classes are in a namespace called ImmutableCollections. I have created persistent versions of some of the collection classes in the System.Collections namespace. I will describe each one and some of the challenges in making them persistent. There are several collection classes that are currently missing; I need to add a queue, for example. Hopefully, I will get to those in time. Also, even though I've taken steps to make these classes efficient, they cannot compete with the System.Collections classes in terms of speed, but they really aren't meant to. They are meant to provide the advantages of immutability while providing reasonable performance.
top
Stack
This one was easy. Simply create a persistent singly linked list and limit insertions and deletions to the head of the list. Since this class is persistent, popping a stack returns a new version of the stack with the next item in the old stack as the new top. In the System.Collections.Stack version, popping the stack returns the top of the stack. The question for the persistent version was how to make the top of the stack available since it cannot be returned when the stack is popped. I chose to create a Top property that represents the top of the stack.
top
SortedList
The SortedList uses AVL tree algorithms to keep the tree in balance. I found it useful to create an IAvlNode interface. Two classes implement this interface, the AvlNode class and the NullAvlNode class. The NullAvlNode class implements the null object design pattern. This simplified many of the algorithms.
top
ArrayList
This is the class that proved most challenging. Like the SortedList, it uses a persistent AVL tree as its data structure. However, unlike the SortedList, items are accessed by index (or by position) rather than by key. I have to admit that the algorithms for accessing and inserting items in a binary tree by index weren't intuitive to me, so I turned to Knuth. Specifically, I used Algorithms B and C in section 6.2.3 in volume 3 of The Art of Computer Programming.
I made an assumption about the ArrayList in order to improve performance. I assumed that the Add method is by far the most used method. However, adding items to the ArrayList one right after the other causes a lot of tree rotations to keep the tree in balance. To solve this, I created a template tree that is already completely balanced. Since this template tree is immutable, it can exist at the class level and be shared amongst all of the instances of the class.
When an instance of the ArrayList class is created, it takes a small subtree of the template tree. As items are added, the nodes in the template tree are replaced with new nodes. Since the tree is completely balanced, no rebalancing is necessary. If the subtree gets filled up, another subtree of equal height is taken from the template tree and joined to the existing tree. Insertions and deletions are handled normally with rebalancing performed if necessary. Again, the assumption is that adding items to the ArrayList occurs much more frequently than inserting or deleting items.
top
Array
The Array class uses the random access list structure to provide a persistent array with logarithmic performance. Unlike a random access list, it has a fixed size.
top
RandomAccessList
This class does not have a parallel in the System.Collections namespace, but it was one of the first persistent classes I wrote, and I decided to include it here. It's a straightforward implementation of Chris Okasaki's random-access list described above. This data structure was designed to be used in functional languages where lists have three basic operations: Cons, Head, and Tail. Cons adds an item to the head of the list, Head is the first item in the list, and Tail represents all of the items in the list except for the Head.
top
Conclusion
Persistent data structures help simplify programming by eliminating a whole class of bugs associated with side-effects and synchronization issues. They are not a cure-all but are a useful tool for helping a programmer deal with complexity. I have explored ways of making data structures persistent and have provided a small .NET library of persistent data structures. I hope you have enjoyed the article, and as always, I welcome feedback.
top
History
02/23/2005 - First version.
Aside from dabbling in BASIC on his old Atari 1040ST years ago, Leslie's programming experience didn't really begin until he discovered the Internet in the late 90s. There he found a treasure trove of information about two of his favorite interests: MIDI and sound synthesis.
After spending a good deal of time calculating formulas he found on the Internet for creating new sounds by hand, he decided that an easier way would be to program the computer to do the work for him. This led him to learn C. He discovered that beyond using programming as a tool for synthesizing sound, he loved programming in and of itself.
Eventually he taught himself C++ and C#, and along the way he immersed himself in the ideas of object oriented programming. Like many of us, he gotten bitten by the design patterns bug and a copy of GOF is never far from his hands.
Now his primary interest is in creating a complete MIDI toolkit using the C# language. He hopes to create something that will become an indispensable tool for those wanting to write MIDI applications for the .NET framework.
Besides programming, his other interests are photography and playing his Les Paul guitars.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 





