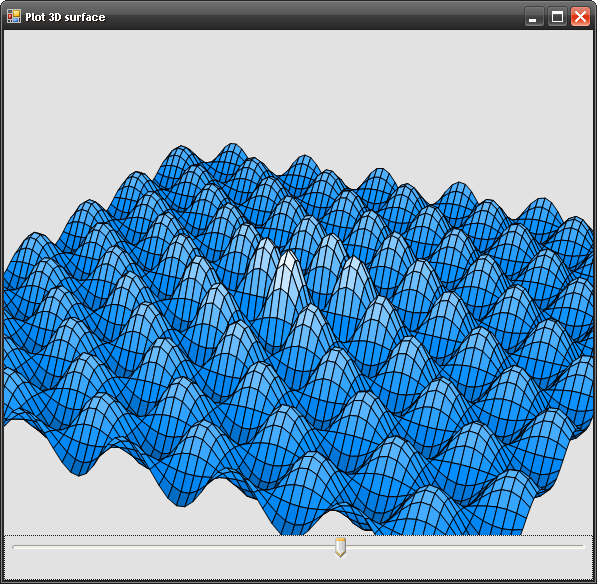
Introduction
This article describes a simple method of rendering 3D surfaces on a 2D plane. It doesn't use OpenGL or DirectX or stuff like that. It just utilizes the power of the CPU. Simplicity has, of course, its price - the rendering process isn't as fast as when using hardware acceleration.
Its application varies from simply admiring beautiful 3D surfaces to data visualization purposes, to stuff whatever one needs. I've used it in programs written for courses of Optimization Methods, Identification, Calculus (Mathematical Analysis), and Dimensional Analysis.
Properties
Density - Size of the spanning mesh.PenColor - Color of the drawing pen. Used to draw meshes.StartPoint - Plotting start point.EndPoint - Plotting end point.Function - Function used to calculate surface vertices.ColorSchema - Color schema assigned to mesh.
Methods
ReCalculateTransformationsCoeficients - Recalculates transformations' coefficients on the basis of new parameters.Project - Performs projection. Calculates screen coordinates for the 3D point.RenderSurface - Main method. Render the surface on given graphics.
Points of Interest
Additional classes
ColorSchema and
CompiledFunction are interesting parts of the code. The first one encapsulates an array of
Color entries. It has some predefined color palettes. The other one compiles a given formula to a function delegate, providing simple parser services.
Usage
Surface3DRenderer sr = new Surface3DRenderer(70, 35, 40,
0, 0, ClientRectangle.Width,
ClientRectangle.Height, 0.5, 0, 0);
sr.ColorSchema = new ColorSchema(120);
sr.SetFunction("sin(x1)*cos(x2)/(sqrt(sqrt(x1*x1+x2*x2))+1)*10");
Use this to actually render something:
sr.RenderSurface(e.Graphics);
And this, whenever plotting area size changes:
sr.ReCalculateTransformationsCoeficients(70, 35, 40, 0, 0,
ClientRectangle.Width, ClientRectangle.Height, 0.5, 0, 0);
Copyright
History
- 22.02.2007 - first version.
- 23.02.2007 - sample images added.
Sample (application)
Below, I'm publishing screenshots from an application that was written for my academic course of Optimization Methods (finding the minimum/maximum of functions). Labels are in Polish, but I hope that they are self-explaining.

Entering the formula:

Finding functions' minimum using the Greatest Slope method:

Michał is C# and whole .NET enthusiast. He graduated from computer science MSc studies at
Wroclaw University of Technology, Poland.
He is interested in photography and diving. He is member of
PADI, currently with divemaster certificate.
His favorite movies are Matrix, Amélie(
Le Fabuleux Destin d'Amélie Poulain), Stargate SG-1 TV Serie and comedies of Mel Brooks.
Michał lives in Wroclaw, Poland. To contact Michał, email him at michal.brylka[mail-'"at'"-sign]op.pl.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 







