Introduction
As I was working on my own little game project, I searched the net for implementations of the A* path finding algorithm in C#, but I could not find any.
There were many, in pretty much every other language, but they either used very language specific features (like templates in C++) or were implemented in a way that just didn't seem very extensible, so I decided to write my own in C#.
I will give a brief introduction to the inner workings of the A* algorithm spiced up with some code samples from the actual implementation. I will also spend a little time explaining how to make your own AStarNode class.
The A* algorithm
There are a few choices in path finding when it comes to algorithms. A* is probably the most popular one, because it is quite flexible.
A* can be used to solve a myriad of different problems, like:
- Combinatory puzzles like Rubric Cube or 8-puzzles.
- Route finding.
- Robot navigation.
- And, of course, path finding in video games, which is what we are going to use it for.
The reason the A* algorithm works so well, is that it favors points that are close to the starting point, and points that are close to the goal as well.
Heuristics
As mentioned earlier, the A* algorithm both favors the distance from the start state (this is called the Cost in the program, traditionally this is called g()) and the estimated distance to the goal (this is called GoalEstimate in the program, traditionally this is called h()).
In my test of the A* class, I let the character move in 8 possible directions on a 2-dimensional map, so I will be using the "Diagonal Distance" approach.
Many different mathematical formulas can be used as heuristic functions when doing an A* search, it all depends on how your character moves.
This article discusses which formula is best used for which movement.
Data structures
Internally the A* algorithm has two lists, the OPEN list, which holds all the nodes that are possible ways to the goal, this is also known as the frontier, and the CLOSED list, which holds all the nodes we have expanded.
Many different data structures are possibly good choices for these lists, but to keep complexity down, I have implemented an "always sorted" array list, that I call Heap. It implements both the IList and IClonable interfaces, even though they are not really used in this project.
The two most important methods relating to the A* search:
public object Pop();
public void Push(object Object);
I am considering tuning this part in a later article, possible using a binary heap as the data structure. More on this later.
Extensibility
The class has been designed to be very extensible. No code in the actual AStarNode class does any calculations relating to coordinates and such, so it should be possible to use this class to solve any A* problem, not just relating to 2-dimensional grids.
Later I will explain how to implement your own child of the AStarNode class.
The actual A* algorithm
The implementation of the A* main loop is pretty straight forward. I will go through it step-by-step and explain what is going on.
First we assign the starting node and the goal node to private variables. These will be used through-out the entire pathfinding. Then we add the starting node as our initial search state:
FStartNode = AStartNode;
FGoalNode = AGoalNode;
FOpenList.Add(FStartNode);
Then we start our main loop. We will keep looping as long as there are still nodes on our heap:
while(FOpenList.Count > 0)
{
Then we get the node with the lowest TotalCost off the OPEN list. Since the heap is always sorted according to the IComparable interface implementation of the AStarNode class, this happens just by popping the value off the heap:
AStarNode NodeCurrent = (AStarNode)FOpenList.Pop();
If the current node is the solution, we will now copy the completed path to the Solution list:
if(NodeCurrent.IsGoal()) {
while(NodeCurrent != null) {
FSolution.Insert(0,NodeCurrent);
NodeCurrent = NodeCurrent.Parent;
}
break;
}
Then we ask the AStarNode child to give us all possible successors of the current node (except the parent of the current node of course):
NodeCurrent.GetSuccessors(FSuccessors);
Then we loop through the successors and see if they are worth anything:
foreach(AStarNode NodeSuccessor in FSuccessors)
{
First we see if the successor node is already on the OPEN list, if it is and the TotalCost is higher than the existing one, we will discard this successor node:
AStarNode NodeOpen = null;
if(FOpenList.Contains(NodeSuccessor))
NodeOpen = (AStarNode)FOpenList[FOpenList.IndexOf(NodeSuccessor)];
if((NodeOpen != null) && (NodeSuccessor.TotalCost > NodeOpen.TotalCost))
continue;
Then we do the exact same thing on the CLOSED list:
AStarNode NodeClosed = null;
if(FClosedList.Contains(NodeSuccessor))
NodeClosed = (AStarNode)FClosedList[FClosedList.IndexOf(NodeSuccessor)];
if((NodeClosed != null) && (NodeSuccessor.TotalCost > NodeOpen.TotalCost))
continue;
Then we remove the instances found on the OPEN and CLOSED list:
FOpenList.Remove(NodeOpen);
FClosedList.Remove(NodeClosed);
Then we add the current successor to the OPEN list and end the loop:
FOpenList.Push(NodeSuccessor);
}
Then last, but not least, we will add the current node to the closed list and end the loop:
FClosedList.Add(NodeCurrent);
}
This concludes the main loop in the A* algorithm. Note, that there are circumstances where this implementation can enter an end-less loop. If, for example, the goal is unreachable. It is easy to implement ways to exit the loop, but I will leave the refinement of the implementation for a later time.
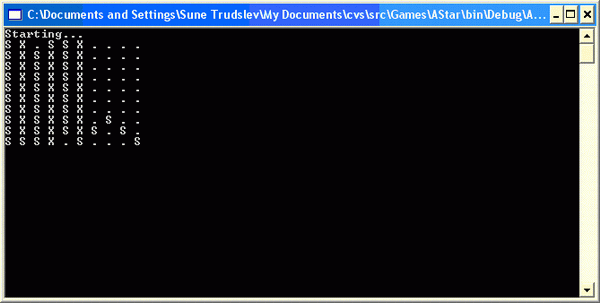
Here's how it looks when you run it with one of the test maps:
Creating your own AStarNode class
To create your own AStarNode descendant, you need to override all the virtual members of the AStarNode class:
public virtual bool IsSameState(AStarNode ANode);
public virtual void Calculate();
public virtual void GetSuccessors(ArrayList ASuccessors);
public virtual void PrintNodeInfo();
The implementation of the IsSameState() method must check all state information (i.e. coordinates), if it's the same state it should return true, otherwise false.
The implementation of the Calculate() method must calculate the GoalEstimate (the heuristic) according the state information and the GoalNode.
The implementation of the GetSuccessors() method must place all possible successors of the node itself on the ASuccessors ArrayList.
The implementation of the PrintNodeInfo() method should print whatever information is available about the state. The current code calls it from the private method PrintNodeList() on the AStar class to print information about the lists. You can place calls to PrintNodeList in strategic places in the code if you want to see what is going on when the code is path finding.
Conclusion
With this class, you should be able to implement A* path finding to your own C# projects. The implementation allows for any kind of A* search to be done. Other people have implemented solving of 8-puzzles using the same generic algorithm.
More information
This article was inspired by other peoples' work:
And for a very interesting graphical look:
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 









