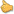

Introduction
According to Wikipedia:"Kruskal's algorithm is an algorithm in graph theory that finds a minimum spanning tree for a connectedweighted graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. If the graph is not connected, then it finds a minimum spanning forest (a minimum spanning tree for each connected component). Kruskal's algorithm is an example of a greedy algorithm."
In short, Kruskal's algorithm is used to connect all nodes in a graph, using the least cost possible.
Example
A cable TV company is laying a cable in a new neighborhood. An internet cafe is connecting all PCs via network.
Using the Demo
Click anywhere to plot the vertices. Hold down ctrl and select two vertices to create an edge. A popup window appears to enter edge cost. Having finished plotting the graph, click Solve.
High Level Design

Low Level Design

Using the Code
IList<Edge> Solve(IList<Edge> graph, out int totalCost);
How the Graph is formed with GDI is not covered as it is irrelevant.
Classes
Typically, our graph consists of two components, Vertices, and Edges connecting these vertices.
Each Edge is marked by a value or weight, which is the Cost of connecting the two vertices.
Vertex
Holds:
- Vertex Name (which must be unique within Graph) and its Drawing Point
- Rank and Root (we'll get to those later)
using System;
using System.Drawing;
namespace Kruskal
{
public class Vertex
{
#region Members
private int name;
#endregion
#region Public Properties
public int Name
{
get
{
return name;
}
}
public int Rank { get; set; }
public Vertex Root { get; set; }
public Point Position { get; set; }
#endregion
#region Constructor
public Vertex(int name, Point position)
{
this.name = name;
this.Rank = 0;
this.Root = this;
this.Position = position;
}
#endregion
#region Methods
internal Vertex GetRoot()
{
if (this.Root != this)
{
this.Root = this.Root.GetRoot();
}
return this.Root;
}
internal static void Join(Vertex root1, Vertex root2)
{
if (root2.Rank < root1.Rank)
{
root2.Root = root1;
}
else
{
root1.Root = root2;
if (root1.Rank == root2.Rank)
{
root2.Rank++;
}
}
}
#endregion
}
}
Edge
Holds two Vertices, Cost of connection between them, and CostDrawing Point.
Note that it implements IComparable, we'll need it to sort Edges by Cost later on.
using System;
using System.Drawing;
namespace Kruskal
{
public class Edge : IComparable
{
#region Members
private Vertex v1, v2;
private int cost;
private Point stringPosition;
#endregion
#region Public Properties
public Vertex V1
{
get
{
return v1;
}
}
public Vertex V2
{
get
{
return v2;
}
}
public int Cost
{
get
{
return cost;
}
}
public Point StringPosition
{
get
{
return stringPosition;
}
}
#endregion
#region Constructor
public Edge(Vertex v1, Vertex v2, int cost, Point stringPosition)
{
this.v1 = v1;
this.v2 = v2;
this.cost = cost;
this.stringPosition = stringPosition;
}
#endregion
#region IComparable Members
public int CompareTo(object obj)
{
Edge e = (Edge)obj;
return this.cost.CompareTo(e.cost);
}
#endregion
}
}
Algorithm Implementation
Sorting Edges
Edges are sorted in ascending order according to Cost using Quick Sort.
Making Sets
Initially, every Vertex is its own Root and has rank zero.
public Vertex(int name, Point position)
{
this.name = name;
this.Rank = 0;
this.Root = this;
this.Position = position;
}
Why This Step?
We need it to ensure that, on adding our Vertices, we are not forming a loop.
Consider this example:

The Edge BD was not considered, because B,D are already connected through B,A,D.
Thus, for every Edge we examine, we must inspect that its two Vertices belong to different sets (trees).
How To Find Out If Two Vertices Are In Different Sets?
Using the recursive function GetRoot().
internal Vertex GetRoot()
{
if (this.Root != this)
{
this.Root = this.Root.GetRoot();
}
return this.Root;
}
If roots are indeed different, (each Vertex is in a different set), Join() the two Vertices.
internal static void Join(Vertex root1, Vertex root2)
{
if (root2.Rank < root1.Rank)
{
root2.Root = root1;
}
else
{
root1.Root = root2;
if (root1.Rank == root2.Rank)
{
root2.Rank++;
}
}
}
Conclusion
Hope I delivered a clear explanation.
Enthusiastic programmer/researcher, passionate to learn new technologies, interested in problem solving, data structures, algorithms, AI, machine learning and nlp.
Amateur guitarist/ keyboardist, squash player.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin