Introduction
This is a sequel of the article called "CodeProject's Article voting system" in which I have discussed two voting models, one of which I thought is used on the CodeProject's website.
As far as I was corrected by Chris Maunder who provided me with the model that is really used, I have decided to analyze this model too.
In this article you will find the rating counting algorithm, the description of its model and then some analysis of it.
Rating counting algorithm
The following description was cut and pasted from the following post "Excellent analysis. Unfortunately not quite correct":
Each article on CodeProject has associated with it a Vote Total (Vt), a Weight Total (Wt), and a number of votes (N). When a member votes, the system adds the weight of their vote (dependant on membership level) to Wt, and the rating itself multiplied by their weight to Vt. The rating of an article is then R = Vt / Wt.
If everyone has a weight of 1 then Wt = N, and R = Vt / N. Having differing weights, though, means that when a gold member (weight = 4) and bronze member (weight = 1) vote, the vote is weighted towards the gold:
Assume Gold votes 5 and Bronze votes 1:
Wt = 4 + 1 = 5
Vt = 4 x 5 + 1 x 1 = 21
R = 4.2
This is quite clear and looks very reasonable as each person has its weight in the system that depends on its status. But does it really works? An answer to this question along with the probability model will be given in the following sections.
Voting probability model
In the algorithm described above we deal with two types of random variables:
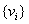 - the peoples' vote values
- the peoples' vote values  - the person's weight in the system
- the person's weight in the system
Note that:
 ,
,  ,
,  and
and  are independent when
are independent when  and
and 
 ,
,  have the same distribution
have the same distribution 
 ,
,  have the same distribution
have the same distribution 
Now we can represent the algorithm given above by the following formula:

In this formula index  means that
means that  is the rating after the
is the rating after the  'th vote. It is also obvious that
'th vote. It is also obvious that  is the weight of the person who put in the
is the weight of the person who put in the  vote and thus voted with the value
vote and thus voted with the value  .
.
Let us now assume that we have the following mean values of our random variables:
 ,
, 

It is well known from the probability theory that for two random variables  and
and  :
:

If they are independent then:

Now we are ready to calculate the following mean value  :
:


(These calculations are trivial and self descriptive)
In other words  and doesn't depend anyhow from weights of the persons who participated in the voting!
and doesn't depend anyhow from weights of the persons who participated in the voting!
It is also interesting to note that if the rating formula would be the following:

then the mean value of the rating would be  i.e. independent from vote values!
i.e. independent from vote values!
Conclusions
In this article I have calculated the mean value of the rating that measures the quality of any article on CodeProject's website.
It was discovered that although the weight of each person in the system is taken into account in case when the vote and the weight are independent, the mean value of rating random variable doesn't depend on the weight. Even more, the mean value is also the same as the mean value for the two other voting models described in my previous article "CodeProject's Article voting system".
Note that if the vote values depend on person's weights then the rating mean value is different and involves the weights distribution. Thus this approach may be considered to be more general than simple approaches that do not involve weights.
References
PhD in Numerical and Statistical Model Checking of Probabilistic systems. Bachelor and Masters degrees (with honors) in Theoretical Mathematics. Thirteen (13) international research publications, among which nine (10) are DBLP recognized. Seventeen (17) years of work experience in Research, Design and Development of Verification Algorithms for Probabilistic and Control Systems, Scientific Software, Embedded Systems and Web applications. Excellent English (TOEFL-257-PC) and Good Dutch (NT2-2) skills. Permanent Dutch residence.
Specialties:
• Theoretical and applied research in Control and Formal Verification (numerical and statistical);
• Acquiring information, sharing knowledge, lecturing, mentoring, motivating and evaluating people;
• Working on large-scale distributed, multi-threaded, event-driven, cross-disciplinary software projects;
Research experiences:
• Numerical and Statistical Model Checking of Markov Chains;
• Type-2 Computable Topological semantics for CTL* on Dynamic Systems;
• Statistical Machine Translation;
• Deterministic and Symbolic-regression based compression of Symbolic controllers;
• Multi-dimensional trajectory planning with position and derivative constraints.
Teaching and supervision:
• 5 years of teaching at Novosibirsk State University, University of Twente, Fontys Hogescholen
• Supervising 3 master students at TU Twente and RWTH Aachen
• Supervising 11+ trainee-ship/internship students at Fontys Hogescholen
• Managing a group of 7 volunteers in the Russian school foundation
• Leading leading 3 project groups at Fontys Hogescholen
Software experiences (years):
• C++ (8), UML (6), Java (5), C (5), Matlab (4), C# (2), Python (1), Mathematica (1)
• GIT (4), SVN (5), Clearcase (4), Clear Quest (4), SCCS (2)
• CMake (3), Make (2), Ant (2)
• CSS (3), HTML (3), JavaScript (2)
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 












