Introduction
This provides a fast Zip code proximity search and forgoes the massive FLOPS required by numerical methods. I would not call it a true distance search since it is an analytical approximation of our non-analytical reality, but it is much better than most of the code you find online that assumes the Earth is a perfect sphere.
This can be very handy for clients who want to get a general idea of how close the business entities are to each other, but don't want to break the bank by paying $8k per year for the MapPoint API, or simply do not need that level of detail or precision.
Zip code data in the US can be bought for $40 a year. Do not trust the latitudes and longitudes that are used by the UN for their LOCODE system, they are highly inaccurate. If you need international location data, you will have to find another source.
Also remember that the centroid latitude and longitudes for Zip codes may fall out of the physical Zip code area, depending on its geometry. As you implement this, keep in mind that its primary purpose is for a fast proximity search, and is based on the foundation of the analytical model behind a GPS interpreter. If you need a true GPS level of precision in your application, I recommend looking at this Code Project article, which uses an existing GPS interpreter for commercial purposes.
Theory
The earth is an oblate spheroid because of the flattening that results from its rotation, as I have depicted using MATLAB. The image is hollowed out so that you can clearly see the difference between this and the spherical model that is used in code online everywhere:
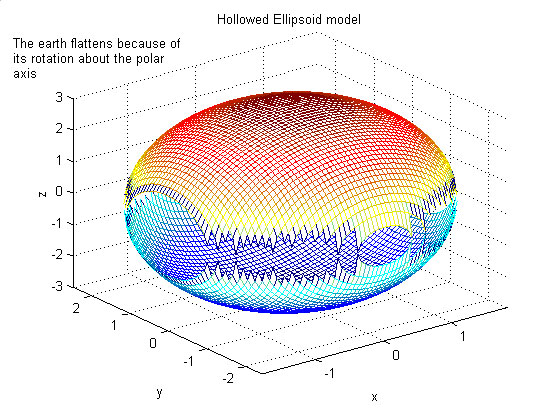
A big problem with many of the searches that you will find online is that this assumption induces great error. You can imagine superimposing a sphere on the image above, and then taking a plane normal to the point of interest. First of all, your 'surface' of the Earth is already greatly exaggerated with a spherical model. Then when you take a normal surface (as many code examples online do, to calculate max and min latitude and longitude), those points on the normal surface are even further exaggerated.
By using the mathematics approved in WGS-84, and used in GPS, we can get a much better approximation. The height above sea level (altitude) is not considered here, because I assume that you do not have topographical data. This is a source of error in the Ellipsoid analytical model, but it also exists in the common spherical model to further exaggerate its mathematical flaws.
The mathematical error of this WGS-84 Ellipsoid model is depicted below:

Remember that the distance is a bird's-eye view in all cases, so you will want to specify that in your search results so that the users don’t confuse this proximity figure with the road/travel distance.
You can obtain postal code latitude/longitude data for $40 a year now, and without paying for a more sophisticated service which maintains road distances, addresses, and altitude data, this is an accurate proximity search that far outperforms the typical 'perfect sphere' model without making your processor cry. Please download the single source code class for all of the gory details. I will only illustrate the concepts in this article.
Extension
Large search radius- If you ever need to search more than 1/4th of the globe, I would recommend breaking this algorithm into pieces instead of throwing an exception. You could handle the search area in a piecewise fashion, with the same analytics here and combine the results upon completion. You would need to determine an optimal frequency for which to create new radii of curvature (then use the local ellipse defined by those radii). With an approach like that, you could break down the curvilinear plane into well defined pieces, without going for a full-blown differential numerical approximation, which would be much more FLOPSy. My guess is that such an extension is purely academic. If you have a requirement for your system to search more than 1/4th of the globe, it's probably a system that requires an unsurpassed level of precision anyway, and it's probably for a client who has $8k per year to blow on the MapPoint API, or some other enterprise solution. Still...as we all know, who can predict what the clients will ask for next? :-) So I thought it was prudent to leave you a breadcrumb trail for this issue. Make sure if you go this route that you accurately model the error and educate your client on it, if you do need to make your way back home from this gingerbread house.
Access to altitude data- If you have altitude data these closed form equations could be modified for better accuracy. You can refer to the WGS-84 manual [927 Kb] to derive your equations. Look at the section on coordinate systems and Geodesy in the appendix.
Data
I'm assuming that you will write the scripting for your own data architecture, so I have replaced my sproc calls and data layer calls. You may also want to find a class online that converts a DataView to a DataTable for sorting purposes. There's a very popular function online for C#, which is easy to find.
The code
The methods are very straightforward. They are well commented, so I will not delve into much detail here. You will have to obtain your own data. The UN maintains 'LOCODE' data that is handy for international business. You will see in the location object some properties that I am taking straight from that data. I recommend using the following tables in your architecture:
- Regions
- Countries
- Subdivisions (International term for States, Provinces, Cantons, etc.)
- Currencies
- Location Entry Criteria
- Counties
- Location (City/Town names and features, optional County FK)
- Postal Codes (with centroid latitude, longitude, LocationID FK)
All of my code of interest is in the Location object which gives me everything I want to know about a place or area on the globe.
#region Declarations
private int regionID;
private string regionName;
private int countryID;
private string countryCode;
private string countryName;
private int primaryCurrencyID;
private string primaryCurrencyCode;
private string primaryCurrencyName;
private int secondaryCurrencyID;
private string secondaryCurrencyCode;
private string secondaryCurrencyName;
private int subdivisionID;
private string subdivisionCode;
private string subdivisionName;
private string subdivisionType;
private int countyID;
private string countyName;
private int locationID;
private string cityName;
private bool hasPort;
private bool hasRailTerminal;
private bool hasRoadTerminal;
private bool hasAirport;
private bool hasBorderCrossing;
private bool hasPostalExchangeOffice;
private string postalCode;
private double longitude;
private double latitude;
private string address;
private string addressee;
#endregion
You can also create a collection of these objects, because I use CollectionBase:
#region Collections
public Location this[int i]
{
get {return (Location)List[i];}
set {List[i] = value;}
}
public void AddLocation(Location L)
{
List.Add(L);
}
public void RemoveLocation(Location L)
{
List.Remove(L);
}
#endregion
Constants that are used in the formulas:
#region Constants
internal int a = 6378137;
internal double e = 0.0066943799901413165;
internal double milesToMeters = 1609.347;
internal double degreesToRadians = Math.PI/180;
#endregion
Now you can use the search postal code to return the latitude and longitude that is the centroid of your search ellipse. The radii of curvature functions determine your reference ellipsoid for the latitude of the search. An exception is thrown if the accuracy is severely compromised by the search parameters.
Function: public DataTable FindNearbyLocations(string centroidPostalCode, double searchRadius, bool isMetric).
double lat0 =
Convert.ToDouble(centroidDT.Rows[0]["Latitude"])*degreesToRadians;
double lon0 =
Convert.ToDouble(centroidDT.Rows[0]["Longitude"])*degreesToRadians;
double Rm = calcMeridionalRadiusOfCurvature(lat0);
double Rpv = calcRoCinPrimeVertical(lat0);
if (Rpv*Math.Cos(lat0)*Math.PI/2 < searchRadius)
{
throw new ApplicationException("Search radius was too great to " +
"achieve an accurate result with this model.");
}
double latMax = (searchRadius/Rm+lat0)/degreesToRadians;
double lonMax = (searchRadius/(Rpv*Math.Cos(lat0))+lon0)/degreesToRadians;
double latMin = (lat0-searchRadius/Rm)/degreesToRadians;
double lonMin = (lon0-searchRadius/(Rpv*Math.Cos(lat0)))/degreesToRadians;
SqlParameter one2 = new SqlParameter("@latMin",System.Data.SqlDbType.Decimal,
9, ParameterDirection.Input, false,
((System.Byte)(18)), ((System.Byte)(5)), "",
System.Data.DataRowVersion.Current, latMin);
SqlParameter two2 = new SqlParameter("@latMax",System.Data.SqlDbType.Decimal,
9, ParameterDirection.Input, false,
((System.Byte)(18)), ((System.Byte)(5)), "",
System.Data.DataRowVersion.Current, latMax);
SqlParameter three2 = new SqlParameter("@lonMin",System.Data.SqlDbType.Decimal,
9, ParameterDirection.Input, false,
((System.Byte)(18)), ((System.Byte)(5)), "",
System.Data.DataRowVersion.Current, lonMin);
SqlParameter four2 = new SqlParameter("@lonMax",System.Data.SqlDbType.Decimal, 9,
ParameterDirection.Input, false,
((System.Byte)(18)), ((System.Byte)(5)), "",
System.Data.DataRowVersion.Current, lonMax);
object[] Param2 = new object[4]{one2,two2,three2,four2};
DataTable resultPostalCodesDT = new DataTable("ResultPostalCodes");
resultPostalCodesDT = helper.ReadOnlySproc(helper.YOUR_CONNECTION,
"dbo.[YOUR_SPROC]",Param2);
resultPostalCodesDT.Columns.Add("DistanceToCentroid",
System.Type.GetType("System.Double"));
if (resultPostalCodesDT.Rows.Count > 0)
{
for (int i=0;i<resultPostalCodesDT.Rows.Count;i++)
{
resultPostalCodesDT.Rows[i]["DistanceToCentroid"] = calcDistanceLatLons(Rm,
Rpv,lat0,lon0,
Convert.ToDouble(resultPostalCodesDT.Rows[i]["Latitude"])*degreesToRadians,
Convert.ToDouble(resultPostalCodesDT.Rows[i]["Longitude"])*degreesToRadians);
if (Convert.ToDouble(resultPostalCodesDT.Rows[i]["DistanceToCentroid"]) >
searchRadius)
{
resultPostalCodesDT.Rows.RemoveAt(i);
i--;
}
}
if (isMetric == false)
{
foreach(DataRow r in resultPostalCodesDT.Rows)
{
r["DistanceToCentroid"] =
Convert.ToDouble(r["DistanceToCentroid"])/milesToMeters;
}
}
resultPostalCodesDT.DefaultView.Sort = "DistanceToCentroid";
DataTable finalResults = new DataTable("finalResults");
finalResults = YOUR_CUSTOM_UTILITY_CLASS.ConvertDataViewToDataTable(
resultPostalCodesDT.DefaultView);
return finalResults;
}
else
{
return null;
}
Here are the functions for your information that involve the radii of curvature and distance calculations:
public double calcRoCinPrimeVertical(double lat0)
{
double Rn = a/Math.Sqrt(1-e*Math.Pow(Math.Sin(lat0),2));
return Rn;
}
public double calcMeridionalRadiusOfCurvature(double lat0)
{
double Rm =
a*(1-e)/Math.Pow(1-e*(Math.Pow(Math.Sin(lat0),2)),1.5);
return Rm;
}
public double calcDistanceLatLons(double Rm, double Rpv, double lat0,
double lon0, double lat, double lon)
{
double distance = Math.Sqrt(Math.Pow(Rm,2)*Math.Pow(lat-lat0,2)+
Math.Pow(Rpv,2)*Math.Pow(Math.Cos(lat0),2)*Math.Pow(lon-lon0,2));
return distance;
}
Broad engineering background, Virginia Tech Alum. Attracted to .NET by the sheer power of the framework and elegance of c#. Work includes analytical system to calculate joint torque during balance recovery to recommend physical therapy routines and correct bad biomechanics (preventative medicine). Assimilated force plate and 3D kinematic data for modeling. First and sole developer ever to fully automate corporate housing quotes, which I built into a larger engine that serves the company's entire enterprise.
Experience with applications architecture, DB design and UML 2.0. Experience with a broad range of applied mathematics, FEM software coding, solid and fluid mechanics. Great knowledge of healthcare and physiology with degree in Mechanical/Electrical/Materials Engineering Theory (Engineering Science and Mechanics) and concentration in biomechanics.
Currently expanding my corporate housing business engine by day. By night I am expanding my software engineering design and construction knowledge, staying in touch with the direction of healthcare management systems, and moving music business technology forward. Microsoft is now working on blowing iTunes out of the water, but my business is making an even bigger revolution that is far beyond just music retail. It strikes at the heart of the music industry's issues, and perhaps we will consider partnering with Microsoft to feed their music retail goals while they feed our music licensing, publishing, and digital decentralization of distribution.
I am the Enterprise Architect at my company and maintain a small but powerful and effective team. I have personally customized CxOne from construx (www.construx.com) for this team. Long live Steve McConnell.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 






![Rose | [Rose]](https://www.codeproject.com/script/Forums/Images/rose.gif)
 .
. 
