Introduction
This article describes how to detect the collision between two moving (2D) polygons. It's not the first tutorial on the topic, however, the tutorials on the net tend to be a bit too complex for a relatively simple problem. The source codes I could find also had too many abbreviations that I don't get, or were crippled with C optimizations. So here, I'll try to keep it as simple as possible. In any case, it should be possible to include the functions presented here to your C# projects quite straightforwardly. The technique can be used to detect collisions between sprites as an alternative to pixel-perfect collisions which are usually too slow.
Background
To detect if two polygons are intersecting, we use the Separating Axis Theorem. The idea is to find a line that separates both polygons - if such a line exists, the polygons are not intersecting (Fig. 1). The implementation of this theorem is relatively simple, and could be summed up in this pseudo code:
- For each edge of both polygons:
- Find the axis perpendicular to the current edge.
- Project both polygons on that axis.
- If these projections don't overlap, the polygons don't intersect (exit the loop).
This can be easily extended to deal with moving polygons by adding one additional step. After having checked that the current projections do not overlap, project the relative velocity of the polygons on the axis. Extend the projection of the first polygon by adding to it the velocity projection (Fig. 2). This will give you the interval spanned by the polygon over the duration of the motion. From there, you can use the technique used for static polygons: if the projections of polygons A and B don't overlap, the polygons won't collide. (NB: However, remember that if the intervals do overlap, it doesn't necessarily mean that the polygons will collide. We need to do the test for all the edges before knowing that.)
Once we have found that the polygons are going to collide, we calculate the translation needed to push the polygons apart. The axis on which the projection overlapping is minimum will be the one on which the collision will take place. We will push the first polygon along this axis. Then, the amount of translation will simply be the amount of overlapping on this axis (Fig. 3).
That is it! Now, each time a collision occurs, the first polygon will nicely slide along the surface of the other polygon.
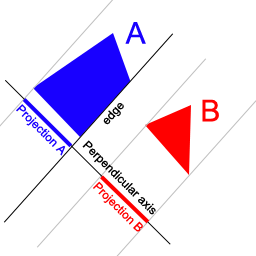
Figure 1: Projections of the polygons onto an axis.
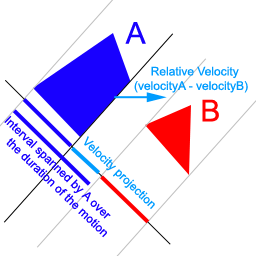
Figure 2: Projections for moving polygons.
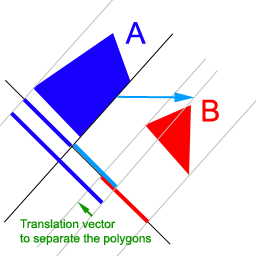
Figure 3: Find the minimum interval overlapping, then calculate the translation required to push the polygons apart.
Using the code
The PolygonCollision() function does all of the above, and returns a PolygonCollisionResult structure containing all the necessary information to handle the collision:
public struct PolygonCollisionResult {
public bool WillIntersect;
public bool Intersect;
public Vector MinimumTranslationVector;
}
Two helper functions are used by the PolygonCollision function. The first one is used to project a polygon onto an axis:
public void ProjectPolygon(Vector axis, Polygon polygon,
ref float min, ref float max) {
float dotProduct = axis.DotProduct(polygon.Points[0]);
min = dotProduct;
max = dotProduct;
for (int i = 0; i < polygon.Points.Count; i++) {
dotProduct = polygon.Points[i].DotProduct(axis);
if (d < min) {
min = dotProduct;
} else {
if (dotProduct> max) {
max = dotProduct;
}
}
}
}
The second one returns the signed distance between two given projections:
public float IntervalDistance(float minA, float maxA, float minB, float maxB) {
if (minA < minB) {
return minB - maxA;
} else {
return minA - maxB;
}
}
Finally, here is the main function:
public PolygonCollisionResult PolygonCollision(Polygon polygonA,
Polygon polygonB, Vector velocity) {
PolygonCollisionResult result = new PolygonCollisionResult();
result.Intersect = true;
result.WillIntersect = true;
int edgeCountA = polygonA.Edges.Count;
int edgeCountB = polygonB.Edges.Count;
float minIntervalDistance = float.PositiveInfinity;
Vector translationAxis = new Vector();
Vector edge;
for (int edgeIndex = 0; edgeIndex < edgeCountA + edgeCountB; edgeIndex++) {
if (edgeIndex < edgeCountA) {
edge = polygonA.Edges[edgeIndex];
} else {
edge = polygonB.Edges[edgeIndex - edgeCountA];
}
Vector axis = new Vector(-edge.Y, edge.X);
axis.Normalize();
float minA = 0; float minB = 0; float maxA = 0; float maxB = 0;
ProjectPolygon(axis, polygonA, ref minA, ref maxA);
ProjectPolygon(axis, polygonB, ref minB, ref maxB);
if (IntervalDistance(minA, maxA, minB, maxB) > 0)\
result.Intersect = false;
float velocityProjection = axis.DotProduct(velocity);
if (velocityProjection < 0) {
minA += velocityProjection;
} else {
maxA += velocityProjection;
}
float intervalDistance = IntervalDistance(minA, maxA, minB, maxB);
if (intervalDistance > 0) result.WillIntersect = false;
if (!result.Intersect && !result.WillIntersect) break;
intervalDistance = Math.Abs(intervalDistance);
if (intervalDistance < minIntervalDistance) {
minIntervalDistance = intervalDistance;
translationAxis = axis;
Vector d = polygonA.Center - polygonB.Center;
if (d.DotProduct(translationAxis) < 0)
translationAxis = -translationAxis;
}
}
if (result.WillIntersect)
result.MinimumTranslationVector =
translationAxis * minIntervalDistance;
return result;
}
The function can be used this way:
Vector polygonATranslation = new Vector();
PolygonCollisionResult r = PolygonCollision(polygonA, polygonB, velocity);
if (r.WillIntersect) {
polygonATranslation = velocity + r.MinimumTranslationVector;
} else {
polygonATranslation = velocity;
}
polygonA.Offset(polygonATranslation);
Reference
History
- September 13, 2006: First version.
- September 14, 2006: Minor changes, and added the Reference section.
Pogopixels is a London based software company specialising in the development of widgets, Flash and internet-based software.
It delivers innovative software solutions to companies using the latest technologies including Adobe AIR, Yahoo Widgets, or Google Desktop.
Have a look at pogopixels.com for more information.
On my spare time, I work on the Appetizer open source project: http://app.etizer.org It's a portable dock for Windows.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 







 give 5 vote
give 5 vote