For years I have seen people struggle with vector mathematics. This guide should walk you through the creation of a reusable Vector3 type in c# and the mathematics behind it all. The post-fixed 3 simply refers to the vector being in 3-dimensions (x,y,z).
The code is not designed to be fast or efficient but is to be as simple and understandable as possible. To this end, and as a personal preference, the Vector3 type is packed with relevent functionality and multiple interfaces to methods (e.g. static and non-static variants of methods). Many would deem this bloated code, however, I think that it makes the code programmer friendly. Obviously, as a projects grows I would tend to refactor functionality back out as I create objects and types for which the functions better fit. I see this as achieving maximum cohesion and minimising coupling and dependencies.
I have used the Cartesian coordinate system in three-dimensions (i.e. three perpendicular axis of x, y and z) and Euclidian geometry. Don't worry about these terms; they are just the formal names for some of the maths covered at senior school. The vector space is volumetric (cube); note that you can use other vector spaces, such as a cylindrical space where one axis (usually z) relates to the radius of the cylinder.
You may have guessed that computers are quite slow with this type of math. Matrix mathematics is more efficient but much harder to understand. You will need a basic grasp of trigonometry and algebra to understand this guide.
Unless stated otherwise I assume that the vector is positional, originating at point (0,0,0). Alternatives to positional vectors are: unit vectors, which can be interpreted as either having no magnitude or an infinite magnitude; and vector pairs where the origin of the vector is another vector, magnitude being a distance from the origin vector.
Please note that this guide is extremely verbose and may seem patronising to experienced C# programmers. Please do not be offended, I have written the guide for a wide audience.
A quick glossary:
- Operator, this is the symbol used to define an operation such as plus (
+) in (a+b) - Operand, these are the variables used in an operation such as (a) and (b) in (a+b). The left-hand-side (LHS) operand is (a) where as the right-hand-side (RHS) operand is (b).
Using the code
To begin with, let us define how the vector information will be stored. I don't often create structs when coding, but for our Vector3 this is perfect. If you are reading this article you probably already know that a vector represents values along a number of axes. For this tutorial we will be developing a three-dimensional type so... thee variables and three axis.
public struct Vector3
{
private readonly double x;
private readonly double y;
private readonly double z;
}
What orientation are the axes in? Being from a visualization background I always assume:
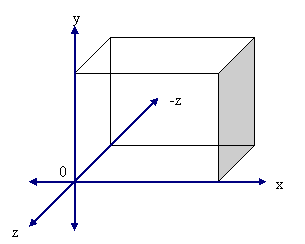
You may have noticed that Z is negative as you look down the axis. This is a common convention in graphics libraries such as OpenGL. This will become important later on when considering pitch, roll and yaw methods.
A quick diversion: Why a struct instead of a class?
The differences between struct and class:
- A struct is a value type created on the stack instead of the heap, thus reducing garbage collection overheads.
- They are passed by value not by reference.
- They are created and disposed of quickly and efficiently.
- You cannot derive other types from them (i.e. non-inheritable).
- They are only appropriate for types with a small number of members (variables). Microsoft recommends a struct should be less than 16 bytes.
- You do not need the new keyword to instantiate a struct.
Basically, it looks like, acts like, and is a primitive type. Although, there is no reason why the vector type could not be created as a class. A drawback of developing a struct is that collection classes in the .NET framework cast structs as classes. This means that a large collection of Vector3's will have a high casting overhead. Generic types were intoduced in C# v2.0 and can be used to reduce the performance cost of casting and boxing structs in collections.
A more in-depth article on structs has been written by S. Senthil Kumar here
Accessing the variables
Did you notice that the variables were private and readonly?
While I have chosen to build a struct, I habitually hide my variables and create public accessor and mutator properties. This is not strictly good practice for structs, but I have created them in case I feel the need to convert to a class at a later date (this is good practice for class structures). In fact, in this type I will not be creating public mutators because a struct should be immutable.
The variables are readonly because this class will be immutable. The x, y, and z variables can only be set when the struct is being constructed. This means that once a Vector3 is built, it will always have the same value. All operations that are performed on the Vector3 will produce another struct. This is important because structs are passed by value which means that they are copied when passed to another method. If you change (or mutate) the values in another method then the changes are lost when you return to the calling method.
In addition to the properties, an array style interface has also been provided. This allows the user call the Vector3 with myVector[x], myVector[y], myVector[z]. Additionally, the user can get all of the components as an array using the Array property.
public double X
{
get{return this.x;}
}
public double Y
{
get{return this.y;}
}
public double Z
{
get{return this.z;}
}
public double[] Array
{
get{return new double[] {x,y,z};}
}
public double this[ int index ]
{
get
{
switch (index)
{
case 0: {return X; }
case 1: {return Y; }
case 2: {return Z; }
default: throw new ArgumentException(THREE_COMPONENTS, "index");
}
}
}
private const string THREE_COMPONENTS =
"Array must contain exactly three components, (x,y,z)";
A property has also been provided to access the magnitude of a vector. The magnitude (or absolute value) of a vector is its length , irrespective of direction and can be determined using the formula:

The SumComponentSquares method (used below) can be seen later in this article.
public double Magnitude
{
get
{
return Math.Sqrt ( SumComponentSqrs() );
}
}
Constructing a Vector3
To construct the type using typical class syntax the following constructor methods have been provided:
public Vector3(double x, double y, double z)
{
this.x = x;
this.y = y;
this.z = z;
}
public Vector3 (double[] xyz)
{
if (xyz.Length == 3)
{
this.x = xyz[0];
this.y = xyz[1];
this.z = xyz[2];
}
else
{
throw new ArgumentException(THREE_COMPONENTS);
}
}
public Vector3(Vector3 v1)
{
this.x = v1.X;
this.y = v1.Y;
this.z = v1.Z;
}
private const string THREE_COMPONENTS =
"Array must contain exactly three components , (x,y,z)";
Operator overloading
We now have a framework for storing, accessing and mutating the Vector3 and its components (x,y,z). We can now consider mathematical operations applicable to a vector. Let's begin by overloading the basic mathematical operators.
Overloading operators allows the programmer to define how a type is used in the code. Take, for example, the plus operator (+). For numeric types this would suggest addition of two numbers. For strings it represents the concatenation of two strings. Operator overloading is of huge benefit to programmers when describing how a type should interact with the system. In C# the following operators can be overloaded:
- Addition, concatenation, and reinforcement (
+) - Subtraction and negation (
-) - Logical negation (
!) - Bitwise complement (
~) - Increment (
++) - Decrement (
--) - Boolean Truth (
true) - Boolean false (
false) - Multiplication (
*) - Division (
/) - Division remainder (
%) - Logical AND (
&) - Logical OR (
|) - Logical Exclusive-OR (
^) - Binary shift left (
<<) - Binary shift right (
>>) - Equality operators, equal and not-equal (
== and !=) - Difference\comparison operators, less-than and greater-than(
< and >) - Difference\comparison operators, less-than or equal-to and greater-than or equal-to(
<= and >=)
Quick Note: MSDN calls this operator overloading, however, what we are doing is more like operator overwriting. If the operators were defined on a base class then we would be using the term operator overwriting.
Addition (v3 = v1 + v2)
The addition of two vectors is achieved by simply adding the x, y, and z components of one vector to the other (i.e. x+x, y+y, z+z).
public static Vector3 operator+(Vector3 v1, Vector3 v2)
{
return new Vector3(
v1.X + v2.X,
v1.Y + v2.Y,
v1.Z + v2.Z);
}
Subtraction (v3 = v1 - v2)
Subtraction of two vectors is simply the subtraction of the x, y, and z components of one vector from the other (i.e. x-x, y-y, z-z).
public static Vector3 operator-(Vector3 v1, Vector3 v2 )
{
return new Vector3(
v1.X - v2.X,
v1.Y - v2.Y,
v1.Z - v2.Z);
}
Negation (v2 = -v1)
Negation of a vector inverts its direction. This is achieved by simply negating each of the component parts of the vector.
public static Vector3 operator-(Vector3 v1)
{
return new Vector3(
-v1.X,
-v1.Y,
-v1.Z);
}
Reinforcement (v2 = +v1)
Reinforcement of a vector actually does nothing but return the original vector given the rules of addition, (i.e. +-x = -x and ++x = +x).
public static Vector3 operator+(Vector3 v1)
{
return new Vector3(
+v1.X,
+v1.Y,
+v1.Z);
}
Other Overloaded Operators
Overloads for the following operators can be found elsewhere in the article:
Comparison
When checking for equality we examine the component parts (x,y,z) of the vectors. When comparing two vectors we compare the magnitude.
Comparing doubles (the magnitude or the component parts of the vector) seems strait forward, the .Net double type provides operators <, >, <=, >=, ==, != and implements IComparable and IEquatable. However, these operations are not reliable. This is because of the way that fractional numbers (i.e. float, double, and decimal variables) are stored in binary representation and the error margin of calculations on them. This gets more complicated when you try to account for special cases numbers: positive and negative 0, positive and negative infinity and Not-A-Number. See Bruce Dawson's article for more information.
There has been a lot of discussion in the comments of this article regarding the use of a threshold when calculating equality. I personally agree with red Baron who suggests that the end user should be responsible for tolerance as it relates to their application:
"... you should not implement a tolerance value inside your code.
What is a suitable value for this tolerance?
It is depending on the problem ..."
Operator signatures cannot be overloaded to take additional parameters so Vector3's comparison operators will remain as intolerant as the double type's operators. When making a comparison between vectors it is recommended that you use <, <=, >, >= with a reasonable tolerance related to the end user application. This is in preference to equality operators ==, != and .Equals. The Equals method, however, can be overloaded.
There are a number of approaches to tolerant comparisons, those described in Bruce Dawson's article are:
- Epsilon comparison / Absolute error tolerance
Best suited for numbers close to 0 - Relative epsilon comparison / Relative error tolerance
Best suited for numbers larger than 0 but difficult to define an appropriate value - Ulp (Units in the Last Place)
Best suited for numbers larger than 0
For the purposes of this article, only absolute error tolerance has been implemented and only as overloads where appropriate. It is important to remember that the operators (<, >, <=, >=, ==, !=) will not accept a tolerance value.
Less-than (result = v1 < v2)
Less-than compares two vectors, returning true only if the magnitude of the left-hand-side vector (v1) is less than the magnitude of the other (v2). To improve efficiency, we do not need to take the final step when calculating the magnitude of a vector, which is to square root the result. The comparison will be the same for the magnitude squared.
public static bool operator<(Vector3 v1, Vector3 v2)
{
return v1.SumComponentSqrs() < v2.SumComponentSqrs();
}
Less-than or Equal-to (result = v1 <= v2)
Less-than or equal-to compares two vectors returning true only if the magnitude of the left-hand-side vector (v1) is less than the magnitude of the other (v2) or the two magnitudes are equal. Again we use the squared magnitude for efficiency.
public static bool operator<=(Vector3 v1, Vector3 v2)
{
return v1.SumComponentSqrs() <= v2.SumComponentSqrs();
}
Greater-than (result = v1 > v2)
Greater-than compares two vectors returning true only if the magnitude of the left-hand-side vector (v1) is greater than the magnitude of the other (v2). Again we use the squared magnitude for efficiency.
public static bool operator>(Vector3 v1, Vector3 v2)
{
return v1.SumComponentSqrs() > v2.SumComponentSqrs();
}
Greater-than or Equal-to (result = v1 >= v2)
Greater-than or equal-to compares two vectors returning true only if the magnitude of the left-hand-side vector (v1) is greater than the magnitude of the other (v2) or the two magnitudes are equal. Again we use the squared magnitude for efficiency.
public static bool operator>(Vector3 v1, Vector3 v2)
{
return v1.SumComponentSqrs() >= v2.SumComponentSqrs();
}
Equality (result = v1 == v2)
To check if two vectors are equal we simply check the component pairs. We AND the results so that any pair which is not equal will result in false.
public static bool operator==(Vector3 v1, Vector3 v2)
{
return
v1.X == v2.X &&
v1.Y == v2.Y &&
v1.Z == v2.Z;
}
If the operator == (equal) is overridden, C# forces us to override != (not-equal). This is simply the inverse of equality.
public static bool operator!=(Vector3 v1, Vector3 v2)
{
return !(v1 == v2);
}
Equals
The Equals method checks for equality between two vectors and implements the IEquitable and IEquatable<Vector3> interfaces provided by the .Net framework. In most cases the result is identical to the == operator. However, one of the special values of a double, the NaN (Not a number), works differently.
- NaN == NaN is false
- NaN.Equals(NaN) is true
This is consistent with the operator == and implementation of .Equals for a double. The reasons for this are described in this article.
public override bool Equals(object other)
{
if(other is Vector3)
{
Vector3 otherVector = (Vector3)other;
return otherVector.Equals(this);
}
else
{
return false;
}
}
public bool Equals(Vector3 other)
{
return
this.X.Equals(other.X) &&
this.Y.Equals(other.Y) &&
this.Z.Equals(other.Z);
}
As mentioned, the Equals method can be overloaded to allow a tolerance value.
public bool Equals(object other, double tolerance)
{
if (other is Vector3)
{
return this.Equals((Vector3)other, tolerance);
}
return false;
}
public bool Equals(Vector3 other, double tolerance)
{
return
AlmostEqualsWithAbsTolerance(this.X, other.X, tolerance) &&
AlmostEqualsWithAbsTolerance(this.Y, other.Y, tolerance) &&
AlmostEqualsWithAbsTolerance(this.Z, other.Z, tolerance);
}
public static bool AlmostEqualsWithAbsTolerance(double a, double b, double maxAbsoluteError)
{
double diff = Math.Abs(a - b);
if (a.Equals(b))
{
return true;
}
return diff <= maxAbsoluteError;
}
GetHashCode
The GetHashCode method is defined on the base class for all objects in C# to provide quick equality comparisons for hash based collections such as Dictionary. Hash code comparisons should produce the same result as the Equals method so we must override GetHashCode when we override the Equals method. For more information see MSDN.
The hash codes of each of the component parts of the vector are bitwise combined with XOR. The prime number 397 is of sufficient size to cause the component hash code to overflow providing a better distribution of hash codes. unchecked stops the compiler from checking for numeric overflow, which in this unusual situation is something we want. There are many valid ways to compute a hash code.
public override int GetHashCode()
{
unchecked
{
var hashCode = this.x.GetHashCode();
hashCode = (hashCode * 397) ^ this.y.GetHashCode();
hashCode = (hashCode * 397) ^ this.z.GetHashCode();
return hashCode;
}
}
CompareTo
The CompareTo method implements a comparison of two vectors which returns:
- -1 if the magnitude is less than the others magnitude
- 0 if the magnitude equals the magnitude of the other
- 1 if the magnitude is greater than the magnitude of the other
This allows the vector type to implement the IComparable and IComparable<Vector3> interfaces provided by the .Net framework.
public int CompareTo(object other)
{
if (other is Vector3)
{
return this.CompareTo((Vector3)other);
}
throw new ArgumentException(
NON_VECTOR_COMPARISON + "\n" +
ARGUMENT_TYPE + other.GetType().ToString(),
"other");
}
public int CompareTo(Vector3 other)
{
if (this < other)
{
return -1;
}
else if (this > other)
{
return 1;
}
return 0;
}
private const string NON_VECTOR_COMPARISON =
"Cannot compare a Vector3 to a non-Vector3";
private const string ARGUMENT_TYPE =
"The argument provided is a type of ";
Again, CompareTo can be overloaded to allow a tolerance value. Here the absolute tolerance calculation is handled by the Equals method overload.
public int CompareTo(object other, double tolerance)
{
if (other is Vector3)
{
return this.CompareTo((Vector3)other, tolerance);
}
throw new ArgumentException(
NON_VECTOR_COMPARISON + "\n" +
ARGUMENT_TYPE + other.GetType().ToString(),
"other" );
}
public int CompareTo(Vector3 other, double tolerance)
{
var bothInfinite =
double.IsInfinity(this.SumComponentSqrs()) &&
double.IsInfinity(other.SumComponentSqrs());
if (this.Equals(other, tolerance) || bothInfinite)
{
return 0;
}
if (this < other)
{
return -1;
}
return 1;
}
Multiplication (dot, cross, and by scalar)
Multiplication of vectors is tricky. There are three distinct types of vector multiplication:
- Multiplication by a scalar (v3 = v1 * s2)
- Dot product (s3 = v1 . v2)
- Cross product (v3 = v1 * v2)
Only multiplication by scalar and division by scalar have been implemented as operator overloads. I have seen operators such as ~ overloaded for the dot product to distinguish it from cross product; I believe that this can lead to confusion and have chosen not to provide operators for dot and cross products leaving the user to call the appropriate method instead.
Multiplication by scalar is achieved by multiplying each of the component parts by the scalar value.
public static Vector3 operator*(Vector3 v1, double s2)
{
return
new Vector3
(
v1.X * s2,
v1.Y * s2,
v1.Z * s2
);
}
The order of operands in multiplication can be reversed; this is known as being commutable.
public static Vector3 operator*(double s1, Vector3 v2)
{
return v2 * s1;
}
The cross product of two vectors produces a normal to the plane created by the two vectors given.

The formula for this (where v1 = A and v2 = B) is



This equation always produces a vector as the result.
The sine of theta is used to account for the direction of the vector. Theta always takes the smallest angle between A and B (i.e.  ).
).
The right hand side of the formula is arrived at by expanding and simplifying the left hand side using the rules:
Sin 0° = 0
Sin 90° = 1
In a matrix style notation this looks like:

You should be aware that this equation is non-commutable. This means that v1 cross-product v2 is NOT the same as v2 cross-product v1.
The C# code for all of this is:
public static Vector3 CrossProduct(Vector3 v1, Vector3 v2)
{
return
new Vector3
(
v1.Y * v2.Z - v1.Z * v2.Y,
v1.Z * v2.X - v1.X * v2.Z,
v1.X * v2.Y - v1.Y * v2.X
);
}
Where possible I have created static methods to extend the programmer's options when making use of the type. Methods which directly affect or are effected by the instance simply call the static methods. As such the instance counterpart of the static method is:
public Vector3 CrossProduct(Vector3 other)
{
return CrossProduct(this, other);
}
Note that this instance method does not affect the instance from which it is called but returns a new Vector3 object. I have chosen to implement cross product in this fashion for two reasons; one, to make it consistent with dot product which cannot produce a vector, and two, because cross product is usually used to generate a normal used somewhere else, the original Vector3 needing to be left intact.
[Side note] A quick template for manually calculating the cross product of two vectors is:

The dot product of two vectors is a scalar value defined by the formula;



The equation should always produce a scalar as the result.
Cosine theta is used to account for the direction of the vector. Theta always takes the smallest angle between A and B (i.e.  ).
).
The right hand side of the formula is arrived at by expanding and simplifying the left hand side using the rules:
Cos 0° =1
Cos 90° = 0
The C# code for this is:
public static double DotProduct(Vector3 v1, Vector3 v2)
{
return
(
v1.X * v2.X +
v1.Y * v2.Y +
v1.Z * v2.Z
);
}
And its counterpart:
public double DotProduct(Vector3 other)
{
return DotProduct(this, other);
}
Division
Division of a vector by a scalar number (e.g. 2) is achieved by dividing each of the component parts by the divisor (s2).
public static Vector3 operator/(Vector3 v1, double s2)
{
return
(
new Vector3
(
v1.X / s2,
v1.Y / s2,
v1.Z / s2
)
);
}
Extended functionality
We now have all the basic functionality required of a Vector3 type. To make this type really useful I have provided additional functionality.
Normalisation and Unit Vector
A unit vector has a magnitude of 1. To test if a vector is a unit vector we simply check for 1 against the magnitude method already defined.
public static bool IsUnitVector(Vector3 v1)
{
return v1.Magnitude == 1;
}
public bool IsUnitVector()
{
return IsUnitVector(this);
}
As this is a comparison we also provide a tolerant overload.
public bool IsUnitVector(double tolerance)
{
return IsUnitVector(this, tolerance);
}
public static bool IsUnitVector(Vector3 v1, double tolerance)
{
return AlmostEqualsWithAbsTolerance(v1.Magnitude, 1, tolerance);
}
Normalization is the process of converting some vector to a unit vector. The formula for this is:

There are a number of special cases that need to be handled when implementing this formula:
- The vector to be normalised has no magnitude.
- The vector to be normalised is already a unit vector.
- The vector to be normalised has one or more components (x,y,z) of NaN.
- The vector has an infinte magnitude and components are all (+/-) infinity or (+/-) 0.
- The vector has an infinite magnitude with real number components.
Mathematically you cannot normalise a vector with a magnitude of 0, however, for convenience to the programmer, many vector implementations will return a zero vector (0,0,0). Similarly, for all of the special cases listed there varying results in the implementations I have found from other libraries.
The first implementation for normalisation that I provide throws exceptions for the special cases except where a mathematically correct value can be provided, for example (infinity, 0, 0) when normalised is (1,0,0).
public static Vector3 Normalize(Vector3 v1)
{
var magnitude = v1.Magnitude;
if (magnitude == 0)
{
throw new NormalizeVectorException(NORMALIZE_0);
}
if (double.IsNaN(magnitude))
{
throw new NormalizeVectorException(NORMALIZE_NaN);
}
if (double.IsInfinity(v1.Magnitude))
{
var x =
v1.X == 0 ? 0 :
v1.X == -0 ? -0 :
double.IsPositiveInfinity(v1.X) ? 1 :
double.IsNegativeInfinity(v1.X) ? -1 :
double.NaN;
var y =
v1.Y == 0 ? 0 :
v1.Y == -0 ? -0 :
double.IsPositiveInfinity(v1.Y) ? 1 :
double.IsNegativeInfinity(v1.Y) ? -1 :
double.NaN;
var z =
v1.Z == 0 ? 0 :
v1.Z == -0 ? -0 :
double.IsPositiveInfinity(v1.Z) ? 1 :
double.IsNegativeInfinity(v1.Z) ? -1 :
double.NaN;
var result = new Vector3(x, y, z);
if (result.IsNaN())
{
throw new NormalizeVectorException(NORMALIZE_Inf);
}
return result;
}
return NormalizeOrNaN(v1);
}
public Vector3 Normalize()
{
return Normalize(this);
}
private static Vector3 NormalizeOrNaN(Vector3 v1)
{
double inverse = 1 / v1.Magnitude;
return new Vector3(
v1.X * inverse,
v1.Y * inverse,
v1.Z * inverse);
}
private const string NORMALIZE_0 =
"Cannot normalize a vector when it's magnitude is zero";
private const string NORMALIZE_NaN =
"Cannot normalize a vector when it's magnitude is NaN";
I have also implemented an alternative method that will behave differently for exceptional conditions. NormalizeOrDefault will return a vector of (0,0,0) if the magnitude is 0 or vector (NaN,NaN,NaN) if any of the components are NaN.
public static Vector3 NormalizeOrDefault(Vector3 v1)
{
if (v1.Magnitude == 0)
{
return Origin;
}
if (v1.IsNaN())
{
return NaN;
}
if (double.IsInfinity(v1.Magnitude))
{
var x =
v1.X == 0 ? 0 :
v1.X == -0 ? -0 :
double.IsPositiveInfinity(v1.X) ? 1 :
double.IsNegativeInfinity(v1.X) ? -1 :
double.NaN;
var y =
v1.Y == 0 ? 0 :
v1.Y == -0 ? -0 :
double.IsPositiveInfinity(v1.Y) ? 1 :
double.IsNegativeInfinity(v1.Y) ? -1 :
double.NaN;
var z =
v1.Z == 0 ? 0 :
v1.Z == -0 ? -0 :
double.IsPositiveInfinity(v1.Z) ? 1 :
double.IsNegativeInfinity(v1.Z) ? -1 :
double.NaN;
var result = new Vector3(x, y, z);
return result.IsNaN() ? NaN : result;
}
return NormalizeOrNaN(v1);
}
public Vector3 NormalizeOrDefault()
{
return NormalizeOrDefault(this);
}
The developer using this Vector3 code should choose the correct overload for their application. The difference is that Normalize will require exception handlers but will tell the developer what the exceptional circumstance was and the NormalizeOrDefault method will allow execution to continue but the calling code must be able to handle the unusual results.
Absolute
The absolute value of a vector is its magnitude. The Abs method has been provided to help programmers who are not aware that the two functions are the same and provide a static interface to the magnitude operator.
public static Double Abs(Vector3 v1)
{
return v1.Magnitude;
}
public double Abs()
{
return this.Magnitude;
}
Angle
This method finds the angle between two vectors using normalization and dot product.




^ refers to a normalized (unit) vector.
|| refers to the magnitude of a Vector.
Due the inherent inprecision of calculations on decimal numbers in a binary system, calculations that should produce an angle of 0 or 1 radian will often be slightly out. To illeviate this, the test for equality and Min have been added to "snap" results back into the correct range. Thanks to Dennis E. Cox in the comments for this solution.
public static double Angle(Vector3 v1, Vector3 v2)
{
if (v1 == v2)
{
return 0;
}
return
Math.Acos(
Math.Min(1.0f, NormalizeOrDefault(v1).DotProduct(NormalizeOrDefault(v2))));
}
public double Angle(Vector3 other)
{
return Angle(this, other);
}
Back-face
This method interprets a vector as a face normal and determines whether the normal represents a back facing plane given a line-of-sight vector. A back facing plane will be invisible in a rendered scene and as such can be except from many scene calculations.


If  then if
then if 
If  then if
then if 
public static bool IsBackFace(Vector3 normal, Vector3 lineOfSight)
{
return normal.DotProduct(lineOfSight) < 0;
}
public bool IsBackFace(Vector3 lineOfSight)
{
return IsBackFace(this, lineOfSight);
}
Distance
This method finds the distance between two positional vectors using Pythagoras theorem.


public static double Distance(Vector3 v1, Vector3 v2)
{
return
Math.Sqrt
(
(v1.X - v2.X) * (v1.X - v2.X) +
(v1.Y - v2.Y) * (v1.Y - v2.Y) +
(v1.Z - v2.Z) * (v1.Z - v2.Z)
);
}
public double Distance(Vector3 other)
{
return Distance(this, other);
}
Interpolation & Extrapolation
This method takes an interpolated value from between two vectors. This method takes three arguments, a starting point (vector v1), and end point (Vector v2), and a control which is a fraction between 1 and 0. The control determines which point between v1 and v2 is taken. A control of 0 will return v1 and a control of 1 will return v2.

n = n1(1-t) + n2t
or:
n = n1 + t(n2-n1)
or:
n = n1 + tn2 -tn1
or:

where:
n = Current value
n1 = Initial value (v1)
n2 = Final value (v2)
t = Control parameter, where  , and where,
, and where,  ,
, 
Extrapolation, where the control value is greter than one or less than 0, is allowed but only if a flag is set. This allows vectors to be returned that sit on the immaginary line that passes through both v1 and v2 but does not have to be between the two.
public static Vector3 Interpolate(
Vector3 v1,
Vector3 v2,
double control,
bool allowExtrapolation)
{
if (!allowExtrapolation && (control > 1 || control < 0))
{
throw new ArgumentOutOfRangeException(
"control",
control,
INTERPOLATION_RANGE + "\n" + ARGUMENT_VALUE + control);
}
return new Vector3(
v1.X * (1 - control) + v2.X * control,
v1.Y * (1 - control) + v2.Y * control,
v1.Z * (1 - control) + v2.Z * control);
}
public static Vector3 Interpolate(Vector3 v1, Vector3 v2, double control)
{
return Interpolate(v1, v2, control, false);
}
public Vector3 Interpolate(Vector3 other, double control)
{
return Interpolate(this, other, control);
}
public Vector3 Interpolate(Vector3 other, double control, bool allowExtrapolation)
{
return Interpolate(this, other, control);
}
private const string INTERPOLATION_RANGE =
"Control parameter must be a value between 0 & 1";
Max and Min
These methods compare the magnitude of two vectors and return the vector with the largest or smallest magnitude respectively.
public static Vector3 Max(Vector3 v1, Vector3 v2)
{
return v1 >= v2 ? v1 : v2;
}
public Vector3 Max(Vector3 other)
{
return Max(this, other);
}
public static Vector3 Min(Vector3 v1, Vector3 v2)
{
return v1 <= v2 ? v1 : v2;
}
public Vector3 Min(Vector3 other)
{
return Min(this, other);
}
Mixed Product
The code for this method was provided by Michał Bryłka. The method calculates the scalar triple product of three vectors. This is the volume of a parallelepiped geometric shape. More information is available on Wikipedia. This method is non-commutable.
public static double MixedProduct(Vector3 v1, Vector3 v2, Vector3 v3)
{
return DotProduct(CrossProduct(v1, v2), v3);
}
public double MixedProduct(Vector3 other_v1, Vector3 other_v2)
{
return DotProduct(CrossProduct(this, other_v1), other_v2);
}
Perpendicular
This method checks if two vectors are perpendicular (i.e. if one vector is the normal of the other).
public static bool IsPerpendicular(Vector3 v1, Vector3 v2)
{
v1 = NormalizeSpecialCasesOrOrigional(v1);
v2 = NormalizeSpecialCasesOrOrigional(v2);
if (v1 == Zero || v2 == Zero)
{
return false;
}
return v1.DotProduct(v2).Equals(0);
}
public bool IsPerpendicular(Vector3 other)
{
return IsPerpendicular(this, other);
}
private static Vector3 NormalizeSpecialCasesOrOrigional(Vector3 v1)
{
if (double.IsInfinity(v1.Magnitude))
{
var x =
v1.X == 0 ? 0 :
v1.X == -0 ? -0 :
double.IsPositiveInfinity(v1.X) ? 1 :
double.IsNegativeInfinity(v1.X) ? -1 :
double.NaN;
var y =
v1.Y == 0 ? 0 :
v1.Y == -0 ? -0 :
double.IsPositiveInfinity(v1.Y) ? 1 :
double.IsNegativeInfinity(v1.Y) ? -1 :
double.NaN;
var z =
v1.Z == 0 ? 0 :
v1.Z == -0 ? -0 :
double.IsPositiveInfinity(v1.Z) ? 1 :
double.IsNegativeInfinity(v1.Z) ? -1 :
double.NaN;
return new Vector3(x, y, z);
}
return v1;
}
Some of the special case logic found in the Normalize method has been extracted into a private class for this slightly different useage. This is simply for code reuse and seperation of concerns.
public static bool IsPerpendicular(Vector3 v1, Vector3 v2, double tolerance)
{
v1 = NormalizeSpecialCasesOrOrigional(v1);
v2 = NormalizeSpecialCasesOrOrigional(v2);
if (v1 == Zero || v2 == Zero)
{
return false;
}
return v1.DotProduct(v2).AlmostEqualsWithAbsTolerance(0, tolerance);
}
public bool IsPerpendicular(Vector3 other, double tolerance)
{
return IsPerpendicular(this, other, tolerance);
}
private static bool AlmostEqualsWithAbsTolerance(
this double a,
double b,
double maxAbsoluteError)
{
double diff = Math.Abs(a - b);
if (a.Equals(b))
{
return true;
}
return diff <= maxAbsoluteError;
}
Projection and Rejection
A vector can be projected onto another using the formula:

Projection is the transformation of a vector on one plane onto another. You can visualise this as shining a light from the pane of the original vector onto a card (the target plane).

Image from: Weisstein, Eric W. "Projection." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Projection.html
Shown with two vectors this looks like:

In the code this is:
public static Vector3 Projection(Vector3 v1, Vector3 v2)
{
return new Vector3(v2 * (v1.DotProduct(v2) / Math.Pow(v2.Magnitude, 2)));
}
public Vector3 Projection(Vector3 direction)
{
return Projection(this, direction);
}
Rejection is the vector representing the change of a vector’s projection to its original value.

The formula for this is simply:

Or

In the code this is:
public static Vector3 Rejection(Vector3 v1, Vector3 v2)
{
return v1 - v1.Projection(v2);
}
public Vector3 Rejection(Vector3 direction)
{
return Rejection(this, direction);
}
Reflection
Reflect a vector about another to provide a mirror image of the original vector.

The formula for this is:

And in code:
public Vector3 Reflection(Vector3 reflector)
{
this = Vector3.Reflection(this, reflector);
return this;
}
public static Vector3 Reflection(Vector3 v1, Vector3 v2)
{
if (Math.Abs(Math.Abs(v1.Angle(v2)) - Math.PI / 2) < Double.Epsilon)
{
return -v1;
}
Vector3 retval = new Vector3(2 * v1.Projection(v2) - v1);
return retval.Scale(v1.Magnitude);
}
Rotation
Euler rotation around axis x,y,z is performed using the methods RotateX, RotateY and RotateZ.
While these methods are unambiguous I prefer the more contextful pitch, yaw, and roll respectively.

Eric__ commented that he would expect a different configuration.
"... Roll, pitch and yaw refer back to the concept of an aircraft's motion.
It is standard notation that X is forward (out the nose), Y is out the right wing and Z is down (toward Earth for level flight).
Therefore it follows that roll is positive about +X, Pitch is positive about +Y (pitch-up means climb), and Yaw is positive around +Z (positive yaw is when the aircraft nose moves to the right)."
To illustrate his point consider the following diagram:

This would appear to make perfect sense. It does! But only when considering the single aeroplane object. When we consider a virtual scene with multiple objects (for example a computer game or virtual reality environment), all objects must be relevant to the user perceiving them. The standard axis for a virtual scene have the user look down the Z axis.

So taking the aeroplane example, it is quite probable that we will be following the aircraft as it flies into the scene:

Hopefully, this explains why the axis are as described and the pitch, yaw, roll configuration is such.
Pitch (RotateX)
RotateX or Pitch rotates a vector around the X axis by a given number of radians (Euler rotation around X).













The hypotenuse (R) cancels out in the equation.
public static Vector3 RotateX(Vector3 v1, double rad)
{
double x = v1.X;
double y = (v1.Y * Math.Cos(rad)) - (v1.Z * Math.Sin(rad));
double z = (v1.Y * Math.Sin(rad)) + (v1.Z * Math.Cos(rad));
return new Vector3(x, y, z);
}
public Vector3 RotateX(double rad)
{
return RotateX(this, rad);
}
public static Vector3 Pitch(Vector3 v1, double rad)
{
return RotateX(v1, rad);
}
public Vector3 Pitch(double rad)
{
return Pitch(this, rad);
}
Yaw (RotateY)
RotateY or Yaw rotates a vector around the Y axis by a given number of degrees (Euler rotation around Y).













The hypotenuse (R) cancels out in the equation.
public static Vector3 RotateY(Vector3 v1, double rad)
{
double x = (v1.Z * Math.Sin(rad)) + (v1.X * Math.Cos(rad));
double y = v1.Y;
double z = (v1.Z * Math.Cos(rad)) - (v1.X * Math.Sin(rad));
return new Vector3(x, y, z);
}
public Vector3 RotateY(double rad)
{
return RotateY(this, rad);
}
public static Vector3 Yaw(Vector3 v1, double rad)
{
return RotateY(v1, rad);
}
public Vector3 Yaw(double rad)
{
return Yaw(this, rad);
}
Roll (RotateZ)
RotateZ or Roll rotates a vector around the Z axis by a given number of radians (Euler rotation around Z).













The hypotenuse (R) cancels out in the equation.
public static Vector3 RotateZ(Vector3 v1, double rad)
{
double x = (v1.X * Math.Cos(rad)) - (v1.Y * Math.Sin(rad));
double y = (v1.X * Math.Sin(rad)) + (v1.Y * Math.Cos(rad));
double z = v1.Z;
return new Vector3(x, y, z);
}
public Vector3 RotateZ(double rad)
{
return RotateZ(this, rad);
}
public static Vector3 Roll(Vector3 v1, double rad)
{
return RotateZ(v1, rad);
}
public Vector3 Roll(double rad)
{
return Roll(this, rad);
}
Arbitary Rotation
Methods to rotate the vector arround a specified point have been implemented. This can also be thought of as offseting the axis before rotation.
public static Vector3 RotateX(Vector3 v1, double yOff, double zOff, double rad)
{
double x = v1.X;
double y =
(v1.Y * Math.Cos(rad)) - (v1.Z * Math.Sin(rad)) +
(yOff * (1 - Math.Cos(rad)) + zOff * Math.Sin(rad));
double z =
(v1.Y * Math.Sin(rad)) + (v1.Z * Math.Cos(rad)) +
(zOff * (1 - Math.Cos(rad)) - yOff * Math.Sin(rad));
return new Vector3(x, y, z);
}
public Vector3 RotateX(double yOff, double zOff, double rad)
{
return RotateX(this, yOff, zOff, rad);
}
public static Vector3 RotateY(Vector3 v1, double xOff, double zOff, double rad)
{
double x =
(v1.Z * Math.Sin(rad)) + (v1.X * Math.Cos(rad)) +
(xOff * (1 - Math.Cos(rad)) - zOff * Math.Sin(rad));
double y = v1.Y;
double z =
(v1.Z * Math.Cos(rad)) - (v1.X * Math.Sin(rad)) +
(zOff * (1 - Math.Cos(rad)) + xOff * Math.Sin(rad));
return new Vector3(x, y, z);
}
public Vector3 RotateY(double xOff, double zOff, double rad)
{
return RotateY(this, xOff, zOff, rad);
}
public static Vector3 RotateZ(Vector3 v1, double xOff, double yOff, double rad)
{
double x =
(v1.X * Math.Cos(rad)) - (v1.Y * Math.Sin(rad)) +
(xOff * (1 - Math.Cos(rad)) + yOff * Math.Sin(rad));
double y =
(v1.X * Math.Sin(rad)) + (v1.Y * Math.Cos(rad)) +
(yOff * (1 - Math.Cos(rad)) - xOff * Math.Sin(rad));
double z = v1.Z;
return new Vector3(x, y, z);
}
public Vector3 RotateZ(double xOff, double yOff, double rad)
{
return RotateZ(this, xOff, yOff, rad);
}
Rounding
These methods round the components of a vector to:
- The nearest integral value:
public static Vector3 Round(Vector3 v1)
{
return new Vector3(Math.Round(v1.X), Math.Round(v1.Y), Math.Round(v1.Z));
}
public static Vector3 Round(Vector3 v1, MidpointRounding mode)
{
return new Vector3(
Math.Round(v1.X, mode),
Math.Round(v1.Y, mode),
Math.Round(v1.Z, mode));
}
public Vector3 Round()
{
return new Vector3(Math.Round(this.X), Math.Round(this.Y), Math.Round(this.Z));
}
public Vector3 Round(MidpointRounding mode)
{
return new Vector3(
Math.Round(this.X, mode),
Math.Round(this.Y, mode),
Math.Round(this.Z, mode));
}
- A specified number of digits:
public static Vector3 Round(Vector3 v1, int digits)
{
return new Vector3(
Math.Round(v1.X, digits),
Math.Round(v1.Y, digits),
Math.Round(v1.Z, digits));
}
public static Vector3 Round(Vector3 v1, int digits, MidpointRounding mode)
{
return new Vector3(
Math.Round(v1.X, digits, mode),
Math.Round(v1.Y, digits, mode),
Math.Round(v1.Z, digits, mode));
}
public Vector3 Round(int digits)
{
return new Vector3(
Math.Round(this.X, digits),
Math.Round(this.Y, digits),
Math.Round(this.Z, digits));
}
public Vector3 Round(int digits, MidpointRounding mode)
{
return new Vector3(
Math.Round(this.X, digits, mode),
Math.Round(this.Y, digits, mode),
Math.Round(this.Z, digits, mode));
}
Scale
This method changes the magnitude of a vector to a specified value without changing the direction.
public static Vector3 Scale(Vector3 vector, double magnitude)
{
if (magnitude < 0)
{
throw new ArgumentOutOfRangeException("magnitude", magnitude, NEGATIVE_MAGNITUDE);
}
if (vector == new Vector3(0, 0, 0))
{
throw new ArgumentException(ORIGIN_VECTOR_MAGNITUDE, "vector");
}
return vector * (magnitude / vector.Magnitude);
}
public Vector3 Scale(double magnitude)
{
return Vector3.Scale(this, magnitude);
}
private const string NEGATIVE_MAGNITUDE =
"The magnitude of a Vector3 must be a positive value, (i.e. greater than 0)";
private const string ORIGIN_VECTOR_MAGNITUDE =
"Cannot change the magnitude of Vector3(0,0,0)";
Component Functions
I have provided a number of functions which target the vectors components. These are not mathematically valid for the vector as a whole. For example, there is no concept of raising a vector to a power (that I know of) however the PowComponents method can be used to raise each of x,y,z to a given power.
Sum components
This method simply adds together the vector components (x, y, z).
public static double SumComponents(Vector3 v1)
{
return (v1.X + v1.Y + v1.Z);
}
public double SumComponents()
{
return SumComponents(this);
}
To Power
This method multiplies the vectors components to a given power.
public static Vector3 PowComponents(Vector3 v1, double power)
{
return
new Vector
(
Math.Pow(v1.X, power),
Math.Pow(v1.Y, power),
Math.Pow(v1.Z, power)
);
}
public void PowComponents(double power)
{
this = PowComponents(this, power);
}
Square root
This method applies the square root function to each of the vectors components.
public static Vector3 SqrtComponents(Vector3 v1)
{
return
(
new Vector3
(
Math.Sqrt(v1.X),
Math.Sqrt(v1.Y),
Math.Sqrt(v1.Z)
)
);
}
public void SqrtComponents()
{
this = SqrtComponents(this);
}
Square
This method squares to each of the vectors components.
public static Vector3 SqrComponents(Vector3 v1)
{
return
(
new Vector3
(
v1.X * v1.X,
v1.Y * v1.Y,
v1.Z * v1.Z
)
);
}
public void SqrComponents()
{
this = SqrtComponents(this);
}
Sum of squares
This method finds the sum of each of the vectors components squared.
public static double SumComponentSqrs(Vector3 v1)
{
Vector3 v2 = SqrComponents(v1);
return v2.SumComponents();
}
public double SumComponentSqrs()
{
return SumComponentSqrs(this);
}
Not A Number
If any of the components (x,y,z) are NaN the whole vector should be considered "Not A Number". This method returns true if any of the components (x,y,z) are NaN.
public static bool IsNaN(Vector3 v1)
{
return double.IsNaN(v1.X) || double.IsNaN(v1.Y) || double.IsNaN(v1.Z);
}
public bool IsNaN()
{
return IsNaN(this);
}
Usability functions
We have seen implementations for the .Net interfaces IComparable, IComparable<Vector3>, and IEquatable<Vector3>. For completeness IFormattable is also implemented. The method defined by the interface, ToString, returns a textual description of the type. VerbString has also been provided to provide a verbose textual description. ToString can accept a numeric format string optionally proceeded by a character x, y or z which indicates the relevant vector component to describe.
public string ToVerbString()
{
string output = null;
if (IsUnitVector())
{
output += UNIT_VECTOR;
}
else
{
output += POSITIONAL_VECTOR;
}
output += string.Format("( x={0}, y={1}, z={2})", X, Y, Z);
output += MAGNITUDE + Magnitude;
return output;
}
private const string UNIT_VECTOR =
"Unit vector composing of ";
private const string POSITIONAL_VECTOR =
"Positional vector composing of ";
private const string MAGNITUDE =
" of magnitude ";
public string ToString(string format, IFormatProvider formatProvider)
{
if (format == null || format == "")
return String.Format("({0}, {1}, {2})", X, Y, Z);
char firstChar = format[0];
string remainder = null;
if (format.Length > 1)
remainder = format.Substring(1);
switch (firstChar)
{
case 'x':
return X.ToString(remainder, formatProvider);
case 'y':
return Y.ToString(remainder, formatProvider);
case 'z':
return Z.ToString(remainder, formatProvider);
default:
return
String.Format
(
"({0}, {1}, {2})",
X.ToString(format, formatProvider),
Y.ToString(format, formatProvider),
Z.ToString(format, formatProvider)
);
}
}
public override string ToString()
{
return ToString(null, null);
}
Standard Cartesian vectors and constants
Finally four standard vector constants are defined:
public static readonly Vector3 Origin = new Vector3(0,0,0);
public static readonly Vector3 XAxis = new Vector3(1,0,0);
public static readonly Vector3 YAxis = new Vector3(0,1,0);
public static readonly Vector3 ZAxis = new Vector3(0,0,1);
And miscellaneous read-only values:
public static readonly Vector3 MinValue =
new Vector3(Double.MinValue, Double.MinValue, Double.MinValue);
public static readonly Vector3 MaxValue =
new Vector3(Double.MaxValue, Double.MaxValue, Double.MaxValue);
public static readonly Vector3 Epsilon =
new Vector3(Double.Epsilon, Double.Epsilon, Double.Epsilon);
public static readonly Vector3 Zero =
Origin;
public static readonly Vector3 NaN =
new Vector3(double.NaN, double.NaN, double.NaN);
Serialization
Vector3 implements the [Serializable] attribute and can therefore be written to file. I suggest the following:
static void Main(string[] args)
{
Vector3 vect = new Vector3(1, 2, 3);
XmlSerializer x = new XmlSerializer(vect.GetType());
x.Serialize
(
new System.IO.FileStream("test.xml", System.IO.FileMode.Create),
vect
);
}
Which produces an XML file containing:
="1.0"
<Vector
xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
xmlns:xsd="http://www.w3.org/2001/XMLSchema">
<X>1</X>
<Y>2</Y>
<Z>3</Z>
<Magnitude>3.7416573867739413</Magnitude>
</Vector>
Summary
We now have a Vector3 type with the following public functionality:
 | Constructors
Vector3(double x, double y, double z)Vector3(double[] xyz)Vector3(Vector v1)
Properties
Operators
this[] Indexer+ - == != * / < > <= >=
Static methods
CrossProduct DotProductMixedProductNormalize IsUnitVector Interpolate Distance Abs Angle Max Min Yaw Pitch Roll IsBackFace IsPerpendicular SumComponents SumComponentSqrs SqrComponents SqrtComponents PowComponents
Methods
AbsAngleCrossProductDistanceDotProductInterpolateIsBackFaceIsNaNIsPerpendicularIsUnitVectorMaxMinMixedProductNormalizePitchPowComponentsProjectionReflectionRejectionRollRotateXRotateYRotateZRoundScaleSqrComponentsSqrtComponentsSumComponentSqrsToVerbStringYaw
Methods Implementing Interfaces
CompareTo Equals ToString GetHashCode
Readonly and constant values
EpsilonMaxValueMinValueNaNOriginxAxisyAxiszAxisZero
|
A quick comparison of some of the common features in a selection of libraries that support vectors in .Net. This article’s code execution speed appears to be somewhere in the middle of the selection.
Some of the faster libraries are using floats not doubles and it should be noted that the cross product result for Math.Net is likely a misunderstanding of the library and should probably be ignored.

Points of Interest
There were a number of resources I used during the development of this article and source code provided, I would like to acknowledge the following:
- CSOpenGL Project - Lucas Viñas Livschitz
- Exocortex Project - Ben Houston
- Essential Mathematics for Computer Graphics - John Vince (ISBN 1-85233-380-4)
- Wolfram Mathworld Website
History
(v1.00-v1.20)
Magnitude methods are now encapsulated in a property- Incorrect serialization attributes have been removed
Equality and IsUnitVector methods allow a toleranceAbs method now returns magnitude- Generic
IEquatable and IComparable interfaces have been implemented IFormattable interface has been implemented- Mixed Product function implemented
- Added and renamed additional component based functions (e.g.
SumComponentSquares) Vector renamed to Vector3
(v1.20-v1.30)
- Square components method was pointing to the square root static method
- Added comments about meaning of comparison operations on two vectors
- Changed references to degrees to radians
- Changed the implementation of
Angle to help avoid NaN results - The
Vector3 class is now immutable, property setters have been removed and mutable methods return a new Vector3 - Updated comments to read better under intellisense.
- Added
Projection, Rejection and Reflection operations - Split up operations into regions
- Added scale operations which used to be accessable through the magnitude mutable property
- Changed the
Equals(object) method to use Equals(Vector3) - Added component rounding operations
- Added rotate arround x, y or z (with or without axis offsets)
- Added
Equals overloads with an absolute tolerace parameters - Added
IsUnitVector overloads with absolute tolerance parameters - Added
IsPerpendicular overloads with absolute toleerance parameters - Added
CompareTo overloads with absolut tolerance parameters - Fixed an infinity issue in the
CompareTo method - Unit testing proved that
NaN == NaN is not the same as Nan.Equals(NaN) - Altered .Equals method to be consistent with the .Net framework - Added
IsNaN methods - Added
NormalizeOrDefault method - Added special cases where we can normalize vectors with infinite components.
IsPerpendicular now uses NormalizeOrDefault to account for special cases of infinty.
Director at RADD Solutions Limited, a software development and consultation company in the UK.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 









