Introduction
In computer systems and in the third millennium, speed is very important. Therefore, the algorithm attempts to design systems that will increase efficiency and speed. In this important role, computer games are entertaining people.
In the design of this game, most of the algorithms used in artificial intelligence and the speed mutual accountability between users and systems is important. Sudoku is one of the games that has its particular fans. This game simply because of the repeated failure to produce high numbers of permutations and variations in the size of the place is special. An integral part of these games have been in newspapers and journals.
Many algorithms have been developed for the production of Othello and Backtracking recursive types that can be pointed and informed search, and more. Implement these algorithms, each has its limits. The program presented in this paper is to incomplete a Sudoku with a lack of resolve in the input table and provide a unique solution. The output of this program is one-hundredth the speed in milliseconds.
This time, the system varies with different structures. But total code and provided solutions are competitive and have good speed. Examples of solutions are implemented in different times and this is visible. It speeds up the code using the search methods like binary search. This article has tried using an array of three-dimensional array of values to help the candidate to be kept informed by the corresponding table, complete with its original element in place.
The original Sudoku solves the following three conditions:
- The value of each column is unique
- The value of each row is unique
- The amount per square N * N is a unique internal
Note: The uniqueness of the meaning of Sudoku irregular, but between one and N is non-repetitive. (In this code, the full two-dimensional array of N = 3, and Table 81 has been assumed.)
Each search is evaluated. Using this technique ensures the uniqueness of each table. Informed by what? The use of algorithms for solving various problems to solve every problem is the hardest part. The algorithms informed use of different solutions is one of the best options for solving problems with limited visibility and space is finite.
Provided that the appropriate selection method can have instant access to your choice, Sudoku short finite set of numbers is repeated with a combination of the above conditions that are in place. To this end, the two-dimensional array can be used for display space. Due to the unique numbers to this point will be replaced, the space needed in the algorithm is considerable. And even arrays with N = 4,5, 6 can easily use this method.
It is recommended to solve the N side of the table with an infinite desire to be avoided because there will be enough space for the auxiliary array. This algorithm is derived from the same characteristic speed. It is inappropriate and unnecessary to repeat it in other programs and remove the speed increases. Informed search algorithms are presented in the chart below:
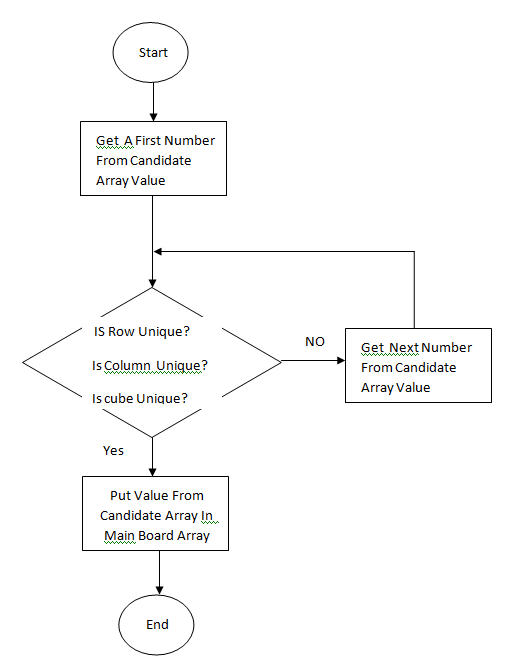
Code Analysis
It is composed of two layers:
- Presentation Layer
- Business Layer
Presentation layer in the array receives constructive input in the Business Class Sudoku sends. This code will see the two classes. It is a two-dimensional array for storing the operating table and uses it on square value of the array's internal default is 3.
The amount varies for different size tables. Also, an internal array of type Bool is used for storing the unique array. These variables are defined as global-level class with a different method of operation that can be performed on these values. The following code is inserted Sudoku incomplete. Zero points in the input string represented in the table are empty.
Sudoku for the complete accuracy of the output is presented. By comparing these values, the user is able to see the correct answer. This code is part of a class of Sudoku and the Fill method to send the missing states. This method is used to fill the array of internal Sudoku.
Presentation Layer Code
Sudoku SUdok = new Sudoku();
string[] SolvedSudoku = new string[81];
string temp1 =
"219876435843591276765243891394157628127368954658429317482735169536914782971682543";
for (int i = 0; i < 81; i++)
{
SolvedSudoku[i] = Convert.ToString(temp1[i]);
}
SUdok.Fill(SolvedSudoku);
lblCompleteSudoko.Text = SUdok.Show();
for (int i = 0; i < 81; i++)
{
SolvedSudoku[i] = "0";
}
string temp =
"219876435803591276065243891394150628127368954658429307482735169536914702970682543";
for (int i = 0; i < 81; i++)
{
SolvedSudoku[i] = Convert.ToString(temp[i]);
}
SUdok.Fill(SolvedSudoku);
These variables have been created and initialized by the constructor of the variables that are defined.
Business Layer Code
public class Sudoku
{
int N = 3;
int[,] board = new int[9, 9];
bool[] checkValue = new bool[10];
public Sudoku()
{
for (int i = 0; i <= (N * N)-1; i++)
{
for (int j = 0; j <= (N * N)-1; j++)
{
board[i, j] = 0;
}
}
for (int i = 0; i <= 9; i++)
{
checkValue[i] = true;
}
}
This method of access to the i, j element two-dimensional array that provides the main table.
public void setSquare(int i, int j, int value)
{
board[i, j] = value;
}
public int getSquare(int i, int j)
{
return board[i, j];
}
This method of displaying two-dimensional table with the three main characters + and - and | are the numbers. Character - a row of | | the intersection of the column and row and column is used.
public string Show()
{
string Temp = string.Empty;
for (int i = 0; i <= (N * N)-1; i++)
{
for (int j = 0; j <= (N * N)-1; j++)
{
if (j % 3 == 0 && j != 0)
{
Temp += " | ";
}
else
{
if (i % 3 == 0 && i != 0 && j == 0)
{
for (int k = 0; k < 18; k++)
{
if (k % 6 == 0 && k != 0)
{
Temp += "+";
}
else
{
Temp += "---";
}
}
Temp += "\r\n";
}
}
if (board[i, j] == 0)
{
Temp += " . ";
}
else
{
Temp += " " + board[i, j] + " ";
}
}
Temp += "\r\n";
}
return Temp;
}
The above-mentioned method for inserting FILL incomplete array of input values used in the original array. FancyFill method for array values as input in excess of incomplete Tues. characters + and - and | are used for display.
public void Fill(string[] lines)
{
int k = 0;
for (int i = 0; i <= (N * N)-1; i++)
{
for (int j = 0; j <= (N * N)-1; j++)
{
board[i, j] = int.Parse(lines[k]);
k++;
}
}
}
public void FancyFill(string[] lines)
{
for (int i = 0; i <= (N * N)-1; i++)
{
for (int j = 0; j <= (N * N)-1; j++)
{
board[i, j] = 0;
}
}
int k = 0;
bool flag = true;
for (int i = 0; i <= (N * N)-1; i++)
{
for (int j = 0; j <= (N * N)-1; j++)
{
flag = true;
for (int l = k; l < lines.Length && flag; l++)
{
if (char.IsDigit(char.Parse(lines[l])))
{
board[i, j] = int.Parse(lines[l]);
flag = false;
}
if (char.Parse(lines[l]) == '.')
{
board[i, j] = 0;
flag = false;
}
k++;
}
}
}
}
IsSolution()
Checks whether or not it is solving Sudoku? For this purpose, it uses four auxiliary functions. The performance of four methods as follows:
IsComplete(): This method is used for all array element.isRowCheckUnique(): This method is unique for all rows of the original array used. isColCheckUnique(): This unique method for all columns is used in the original array. isCubeUnique(): This method is unique for each of the 3 × 3 cube built.
The four were Sudoku solving methods if the answer is True.
public bool isSolution()
{
if (isComplete() && isRowCheckUnique() && isColCheckUnique() && isCubeUnique())
{
return true;
}
return false;
}
public bool isComplete()
{
for (int i = 0; i <= (N * N)-1; i++)
{
for (int j = 0; j <= (N * N)-1; j++)
{
if (!(board[i, j] <= 9 && board[i, j] >= 1))
{
return false;
}
}
}
return true;
}
public bool isRowCheckUnique()
{
for (int i = 0; i <= (N * N)-1; i++)
{
for (int j = 0; j <= (N * N)-1; j++)
{
if (checkValue[board[i,j]] == true)
{
checkValue[board[i,j]] = false;
}
else
{
return false;
}
}
for (int k = 0; k <= 9; k++)
{
checkValue[k] = true;
}
}
return true;
}
public bool isColCheckUnique()
{
for (int i = 0; i <= (N * N)-1; i++)
{
for (int j = 0; j <= (N * N)-1; j++)
{
if (checkValue[board[i,j]] == true)
{
checkValue[board[i,j]] = false;
}
else
{
return false;
}
}
for (int k = 0; k <= 9; k++)
{
checkValue[k] = true;
}
}
return true;
}
public bool isCubeUnique()
{
#region iscubeunique
for (int i = 0; i <= 2; i++)
{
for (int j = 0; j <= 2; j++)
{
checkValue[0] = true;
if (checkValue[board[i, j]] == true)
{
checkValue[board[i, j]] = false;
}
else
{
return false;
}
}
}
for (int k = 0; k <= 9; k++)
{
checkValue[k] = true;
}
for (int i = 0; i <= 2; i++)
{
for (int j = 3; j <= 5; j++)
{
checkValue[0] = true;
if (checkValue[board[i, j]] == true)
{
checkValue[board[i, j]] = false;
}
else
{
return false;
}
}
}
for (int k = 0; k <= 9; k++)
{
checkValue[k] = true;
}
for (int i = 0; i <= 2; i++)
{
for (int j = 6; j <= 8; j++)
{
checkValue[0] = true;
if (checkValue[board[i, j]] == true)
{
checkValue[board[i, j]] = false;
}
else
{
return false;
}
}
}
for (int k = 0; k <= 9; k++)
{
checkValue[k] = true;
}
for (int i = 3; i <= 5; i++)
{
for (int j = 0; j <= 2; j++)
{
checkValue[0] = true;
if (checkValue[board[i, j]] == true)
{
checkValue[board[i, j]] = false;
}
else
{
return false;
}
}
}
for (int k = 0; k <= 9; k++)
{
checkValue[k] = true;
}
for (int i = 3; i <= 5; i++)
{
for (int j = 3; j <= 5; j++)
{
checkValue[0] = true;
if (checkValue[board[i, j]] == true)
{
checkValue[board[i, j]] = false;
}
else
{
return false;
}
}
}
for (int k = 0; k <= 9; k++)
{
checkValue[k] = true;
}
for (int i = 3; i <= 5; i++)
{
for (int j = 6; j <= 8; j++)
{
checkValue[0] = true;
if (checkValue[board[i, j]] == true)
{
checkValue[board[i, j]] = false;
}
else
{
return false;
}
}
}
for (int k = 0; k <= 9; k++)
{
checkValue[k] = true;
}
for (int i = 6; i <= 8; i++)
{
for (int j = 0; j <= 2; j++)
{
checkValue[0] = true;
if (checkValue[board[i, j]] == true)
{
checkValue[board[i, j]] = false;
}
else
{
return false;
}
}
}
for (int k = 0; k <= 9; k++)
{
checkValue[k] = true;
}
for (int i = 6; i <= 8; i++)
{
for (int j = 3; j <= 5; j++)
{
checkValue[0] = true;
if (checkValue[board[i, j]] == true)
{
checkValue[board[i, j]] = false;
}
else
{
return false;
}
}
}
for (int k = 0; k <= 9; k++)
{
checkValue[k] = true;
}
for (int i = 6; i <= 8; i++)
{
for (int j = 6; j <= 8; j++)
{
checkValue[0] = true;
if (checkValue[board[i, j]] == true)
{
checkValue[board[i, j]] = false;
}
else
{
return false;
}
}
}
for (int k = 0; k <= 9; k++)
{
checkValue[k] = true;
}
return true;
#endregion
}
Three-dimensional Array InnerCandidateValue
This array is used to hold element values for each candidate. Considering the original 81 houses, each array must have some unique value in a three-dimensional array with the values placed in the correct position is this.
int[,,] InnerCandidateValue = new int[10, 10, 11];
FillCandidateValue()
This method is used to fill the array of candidates for conservative values.
public void FillcandidateValue()
{
for (int i = 0; i < 10; i++)
{
for (int j = 0; j < 10; j++)
{
for (int k = 0; k < 11; k++)
{
InnerCandidateValue[i, j, k] = k;
}
}
}
}
SolvedSudoku()
This method is used to solve Sudoku incomplete. This program is part of the method. In this method, the number of incomplete element main array of the array is a candidate. The three conditions were the main Sudoku array of candidates for the correct amount placed on the next blank. The array of candidates to replace the new value should be checked again. Finally, the correct amount is in the blank element and informed seek to solve Sudoku.
public void SolvedSudoku()
{
FillcandidateValue();
for (int i = 0; i <= (N * N) - 1; i++)
{
for (int j = 0; j <= (N * N) - 1; j++)
{
if (board[i, j] == 0)
{
for (int l = 0; l <= 8; l++)
{
board[i, j] = InnerCandidateValue[i, j, l+1];
if ((isOneRowCheckUniqe(i) && isOneColCheckUniqe(j) && isCubeUnique()))
{
l = 10;
}
}
}
}
}
}
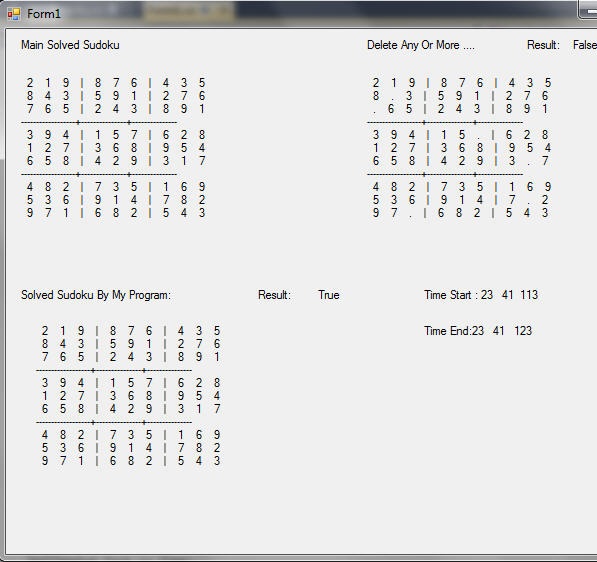
Finally, the presentation layer will display the full amount. This is shown next to an empty array. Finally, solving an array of programs is displayed. The function of each table IsSolution() to check and ensure the correctness of the program is placed. Also at the beginning and end, time in milliseconds is displayed on the system until the problem is presented.
OutPut.Text = SUdok.Show();
lblissolution.Text = Convert.ToString(SUdok.isSolution());
SUdok.SolvedSudoku();
lblissolution2.Text = Convert.ToString(SUdok.isSolution());
lblOutput2.Text = SUdok.Show();
Time = string.Empty;
Time = DateTime.Now.Minute.ToString() + " " +
DateTime.Now.Second.ToString() + " " + DateTime.Now.Millisecond.ToString();
lblTimeEnd.Text += Time;
Using the Code
To use the code to create a Windows Forms project and add to the Sudoku class, an input value of the class is put in the variable Temp. For example, a truncated version of Sudoku has been placed in this variable.
The output format is shown below:
History
- Posted: July 18, 2011, 13:00 PM
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin