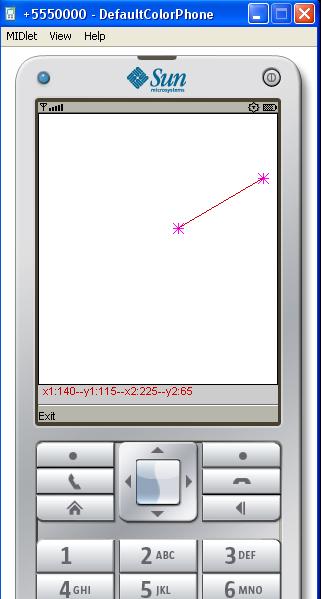
Figure 1
Introduction
The DDA_Final application is capable of drawing lines between two points specified on the screen by the user.
The user can navigate
the cursor on the mobile screen by RIGHT, LEFT, UP, and DOWN keys and specify the end points by pressing the FIRE button.
A line will be drawn on the screen
when both start and end points will be specified. The program was tested on Sun WTK 2.5.2_01 emulator and Nokia 5130XpressMusic Handset.
The reason for implementing the algorithm in J2ME is that the reader gets a glimpse of how the real display devices work. To fully understand the topic, a little knowledge
of computer graphics primitives like pixels and raster display devices is necessary. As the code is written in J2ME, a little knowledge of J2ME will be helpful.
Background
Digital Differential Analyzer or simply abbreviated as DDA line drawing algorithm is used for drawing lines in raster graphics
devices. In this algorithm, the starting and end position of the line has to be supplied.
The intermediary pixel positions will be calculated by the linear interpolation of variables over an interval between
the start and end points. The algorithm is as follows:
Let the start and end point of the line be (x1, y1) and (x2, y2), respectively. So slope, m= (y2-y1)/(x2-x1). Depending on the value of m and
the Quadrant to which (x, y) belongs, intermediary pixel positions have to be calculated as follows:
The positions have to be calculated as follows:
| Quadrant | m<=1 | m>1 |
| First | x=x+1
y=y + m
| x=x+1/m
y=y+1
|
| Second
| x=x-1
y=y + m
| x=x+1/m
y=y+1
|
| Third
| x=x-1
y=y-m
| x=x-1/m
y=y-1
|
| Fourth
| x=x+1
y=y + m
| x=x-1/m
y=y-1
|
| Table-1
|
Here the values of x and y are approximated to the nearest integer value as the pixel position cannot be a floating point number.
This was the theoretical approach towards the algorithm where a point can lie in any of the four quadrants virtually. Practically this is not possible as
the pixel position cannot be negative in physical display devices. In physical display devices we have only the 1st quadrant of the Cartesian axis
system where both x and y are positive or equal to zero and can assume integer values. At the time of implementing the algorithm for physical display devices,
we only have to program for the first quadrant.
Another point to be noted here is that the orientation of physical display devices is different from
the geometrical Cartesian axis.

Figure 2
In the real co-ordinate system for the first quadrant, the x value increases in right direction and y-value increases towards
up continuously. In the physical display device coordinate system, the origin is the top left corner pixel. It means that the top left corner pixel will have
a coordinate value (0, 0). The x co-ordinate value will increase in the right direction pixel wise and
the y co-ordinate value will increase in the downward
direction pixel wise. It may be noted that the bottom-right corner pixel will have
the highest co-ordinate value in the display device.
For a clear visualization, the screen co-ordinate can be viewed as the reflected version of the geometrical first quadrant where
the reflection is done by the line y=0.
Using the Code
A total of five classes are used in the whole program:
Main.java
GUI.java
Cursor.java
DDAEngine.java
DDA.java
Main.java and GUI.java are used to create the Graphical User Interface and Command Actions.
Cursor.java defines the navigable cursor which
is used to select the start and end points. The J2ME Sprite class is used to create the animation.
In DDAEngine.java, the instance for the Cursor is created:
private Cursor c;
. . . . . . . .
public DDAEngine(. . . .){
c=new Cursor(CURSOR_IMAGE,CURSOR_WIDTH,CURSOR_HEIGHT);
c.setRefPixelPosition(height/2, width/2);
this.append(c);
}
The cursor can be navigated throughout the view port using the RIGHT, LEFT, UP, and DOWN keys:
if ((keyState & gui.RIGHT_PRESSED) != 0){
c.moveRight(width);
}
if ((keyState & gui.LEFT_PRESSED) != 0){
c.moveLeft();
}
if ((keyState & gui.UP_PRESSED) != 0){
c.moveUp();
}
if ((keyState & gui.DOWN_PRESSED) != 0){
c.moveDown(height);
}
The cursor on pressing the FIRE button selects the start and end points, respectively:
if ((keyState & gui.FIRE_PRESSED) != 0){
if(!s1){
x1=c.getRefPixelX();
y1=c.getRefPixelY();
s1=true;
hit=false;
. . . . . . . ..
}
if( hit & !s2 ){
x2=c.getRefPixelX();
y2=c.getRefPixelY();
s2=true;
. . . . . . . . . .
}
}
if(s1){
hit=true;
}
When we have both the points selected, the DDA algorithm is invoked from the
DDAEngine.java class which is implemented in the DDA.java class.
if(s1 & s2){
dda=new DDA(x1,y1,x2,y2);
}
In the DDA.java class, we have the drawLine() method which calculates the intermediary pixel positions between (x1, y1) and (x2, y2). Here at the
1st place we calculate the differences between the x and y coordinates of the start and end points:
void drawLine(. .. . ){
dx=(double)(x2-x1);
dy=(double)(y2-y1);
. . . . . . . ..
}
Next we have to check if slope <= 1 or slope > 1:
void drawLine(. .. . ){
. . . . . . . ..
len=Math.abs(dx);
if(Math.abs(dy)>Math.abs(dx))len=Math.abs(dy);
. . . . . . . . .
}
We can model the algorithm in such a way that it works for lines having slope = 90 degrees. The slope of a line is 90 degree means the x co-ordinates of the start and end points
are equal. This can be modeled as:
void drawLine(. .. . ){
. . . . . . . ..
if((x1==x2)&& dy<0)len=dy;
. . . . . . . . .
}
Next select the raster unit, i.e., compute the x-increment and y-increment:
void drawLine(. .. . ){
. . . . . . . ..
xinc=dx/len;
yinc=dy/len;
if((x1==x2)&& dy<0)yinc=Math.abs(dy)/len;
. . . . . . . . .
}
Here one point to be noted is that either xinc or yinc will be one because
len is either (x2-x1) or (y2-y1).
Thus the incremental value for x or y will be one.
Next, calculate and plot the intermediary points by executing a loop:
void drawLine(. .. . ){
. . . . . . . ..
fx=(double)x1;
fy=(double)y1;
double i=1;
if(x1!=x2){
while(i<=len){
g.setColor(200,0,0);
g.drawLine((int)Math.floor(fx),(int)Math.floor(fy),
(int)Math.floor(fx),(int)Math.floor(fy));
fx=fx+xinc;
fy=fy+yinc;
i=i+1;
}
}
else if(x1==x2){
i=(double)y1;
while(i!=(double)y2){
g.setColor(200,0,0);
g.drawLine((int)Math.floor(fx),(int)Math.floor(fy),
(int)Math.floor(fx),(int)Math.floor(fy));
fx=fx+xinc;
fy=fy+yinc;
i=i+yinc;
}
}
. . . . . . . . .
}
The whole project is composed using NetBeans IDE 6.9.1. On successful execution, the user will get a star like cursor on the screen like
in Figure 3.

Figure: 3
This cursor can be navigated by pressing the RIGHT, LEFT, UP, and DOWN Keys. On pressing
Fire the points will be specified on the screen with a pink star as shown in Figure 4.

Figure 4
In figure 4, the start point is specified. On specifying the end point, the line will be drawn as shown in Figure 1. The start and end co-ordinates will also be shown.
Points of Interest
With this program, the difference between geometric and screen coordinates becomes visible to the programmer. Also, this gives a taste to the reader of how
simple graphical contents can be created for real devices.
This member has not yet provided a Biography. Assume it's interesting and varied, and probably something to do with programming.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 





