Introduction
This library provides several classes to work with units of measure, and this as near as possible to the SI standard. It gives the ability to load unit definitions from XML, to parse units, transform them and do calculations with them. Derived units like "km/h" are supported and can be constructed dynamically by dividing the unit "km" through "h". Beside shifted units like "Fahrenheit" and "Celsius", even custom units can be added. The attached demo project demonstrates, how to import self-updating currency units from the Internet. Thus, you can convert "l/EUR" into "cm^3/USD" by using up-to-date currency rates.
Since the library itself is fully XML documented, I will confine myself to the essentials.
This library is part of the Units of Measure Validator for C#.
Concept of Units
There are three different types of units: Base units, scaled/shifted units and derived units.
Each unit has an optional name and an abbreviation. The abbreviation is required for units that are registered to an unit parser, and for base units, since the abbreviation defines the identity of a base unit.
Base units cannot be shortened or constructed from other units. An example is "Meter" or "Second". Two base units are equal, if their abbreviations are equal.
Scaled/Shifted units consists of a factor, an offset and an underlaying unit. An example is "Kilometer", which is 1000 "Meter". The underlaying unit can be any unit type, so you can define the unit "hour" as 60 minutes, and a minute as 60 seconds. Two scaled/shifted units are equal, if they have the same coherent unit and the same factor and offset in relation to this coherent unit. So "30 min" is equal to "half-an-hour", considering "min" is registered as "60 s" and "half-an-hour" as "0.5 hour", "30 min" or "1800 s" - all three options are possible. The offset is needed for unproportional units like degrees Fahrenheit or degrees Celsius. The coherent unit of Fahrenheit and Celsius is Kelvin.
Derived units are composed units with multiple parts, whereas each part consists of a unit of any type and an exponent. An example is "km/h", which is the same as "km^1 * h^-1" or "liter", which is the same as "dm^3". A derived unit is coherent, if all parts are coherent except for scaled/shifted unit parts: If a scaled/shifted unit is unproportional (i.e. an offset different from 0), its coherent unit is (but only for derived units) the most underlaying unit with the same offset. Thus, the coherent unit of cm/µ°C (centimeter per microcelsius) is m/°C, and not m/°K. This is, because a transformation from quantity a in m/°C to b in m/°K is not possible (see the chapter "Shifted Units in Connection with Derived Units").
A special case is the base unit Dimensionless unit, whose abbreviation is "1"
All units inherits from the Unit class, the dimensionless unit is represented by the static and read only Unit.Dimensionless property.
Units can be exponentiated, multiplied and divided using Unit.Pow(int), * and /.
Transformations
A QuantityTransformation describes a transformation for a value in one unit to another. Two transformations can be chained, if the target unit of the first transformation is equal to the source unit of second. Such a chained transformation describes a transformation from the very first unit to the very last.
With Reverse, each transformation can be reversed, so that the source unit and the target unit are exchanged. A transformation from meter to kilometer returns a transformation from kilometer to meter.
The LinearQuantityTransformation class is a QuantityTransformation and describes linear transformations like "Transform(value) = Factor * value + Offset".
Two transformations are equal, if their target units are equal and the mathematical transformation is the same. Two non-base units are equal, if their transformations to their coherent units are equal.
What are Coherent Units?
A coherent unit does not need any factors (or offsets) to express relationships to other coherent units. All base units are coherent.
For example, the definition of newton:
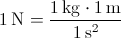 ,
,
all these units are coherent, thus, newton is coherent too.
It would be possible to define 1 newton' as
 ,
,
but since gram is no coherent unit, this definition is not coherent, as well as definitions containing any factors like
 .
.
Nevertheless, it is possible to transform 1 newton' to the coherent newton by multiplying with 1000. This way, the unit of measure library can determine the equality between N' and N''.
Parsing Units
Several formats are supported through different unit parsers, each of them implements IUnitParser. If parsing fails, either null is returned or a format exception will be thrown, depending on the throwFormatException parameter.
Registered Unit Parser
This parser implements IUnitParser and IUnitRegistry and uses a string-unit dictionary to find the corresponding unit for a given string. "1" as dimensionless unit is registered by default.
Prefixed Unit Parser
This parser is capable of parsing strings like "km" or "THz" by going through all available prefixes in the Prefix class and delegating the parsing of the underlaying unit ("m" for "km" or "Hz" for "THz") to an other parser (e.g. the Registered Unit Parser).
Scaled Shifted Unit Parser
The Scaled Shifted Unit Parser parses strings consisting of a factor and a unit abbreviation (e.g. "60 s", the definition for 1 minute). The unit abbreviation is resolved through an injected IUnitParser. It is recommended to use a Composed Unit Parser, containing both a Registered Unit Parser and a Prefixed Unit Parser.
Derived Unit Parser
With this parser, unit expressions like "m^2 * s^-1 / kg^2 * K" can be parsed.
The whitespaces are optional, and if the exponent is equal to 1, the exponent is optional too. Every exponent right from "/" is inverted. Although it is mathematically not correct, it looks much clearer without the braces (unless you convince me of the contrary in your comments).
The parsing of abbreviations is delegated to an injected IUnitParser as for the Scaled Shifted Unit Parser. It is recommended too, to use a Composed Unit Parser, containing both a Registered Unit Parser and a Prefixed Unit Parser.
Composed Unit Parser
The composed unit parser aggregates multiple IUnitParser instances and returns the first successful result. This way, all the mentioned parsers can be combined into a single one.
The method GetUnitRegistry returns the first instance implementing the IUnitRegistry interface (or null if no such instance exists), so new units can be registered quickly into a composed unit parser.
The static method NewDefaultUnitParser returns a fully usable unit parser containing all parsers mentioned above.
CachedUnitParser
This parser delegates the parsing to an injected unit parser and caches the result (the cache will not be emptied automatically).
Loading Unit Definitions from XML
The class XmlUnitLibrary parses an XML document and loads the units into an IUnitRegistryHDUnitsOfMeasure project.
Generally, the XML document looks like:
="1.0"="utf-8"
<UnitLibrary xmlns="http://www.hediet.de/xsd/unitlibrary/1.0">
<BaseUnit Name="Kelvin" Abbr="K"/>
<ScaledShiftedUnit Name="Celsius" Abbr="°C"
Factor="1" Offset="273.15" UnderlayingUnit="K" />
<ScaledShiftedUnit Name="Celsius" Abbr="°F"
Factor="0.55555555555555555555" Offset="255.37222222222222222222"
UnderlayingUnit="K" />
<DerivedUnit Name="Meters per Second" Abbr="mps">
<UnitPart Unit="m" Exponent="1" />
<UnitPart Unit="s" Exponent="-1" />
</DerivedUnit>
</UnitLibrary>Threadsafety
In principle, using this library is thread safe, since each Unit is immutable or the access to members is synchronized. Parsing units is thread safe too as well as using the global unit parser.
Demo
The attached C# demo project demonstrates, how to use the default units and import self-updating currency units from the Internet. You can enter a value, a source unit and a target unit. If a conversion is possible, the result will be displayed.
Shifted Units in Connection with Derived Units
Generally, the transformation from one unit (x) to the underlaying (f) can be expressed by a function f(x).
Scaled/shifted units are described through
 .
.
A unit is unproportional, if its offset is different from 0. This becomes a problem as soon multiple units are combined.
Assuming g(z):
 .
.
If a value v is given in the unit x/z (1v = 1x/z), its transformation to v' in the unit f/g (1v' = 1f/g) can be described as:
 .
.
Only if x and z are given or offset is 0, v' can be calculated.
Assuming offset is zero (if the unit x is proportional):
 .
.
So if unproportional units are used in connection with derived units, they cannot be converted to their coherent equivalent. Nevertheless, µ°C (microcelsius) can be converted to °C, thus °C is the coherent unit for µ°C, if it is part of a derived unit (annotation: standalone, a transformation from µ°C to K is still possible).
For this purpose, the interface ICouldBeUnproportional has been introduced. Units which implement this interface, provides methods to get a proportional transformation to a "coherent" unit.
In principle, it is even not allowed to add two units with an offset:
1 °C + 1 °C = 274 K + 274 K = 548 K = 275 °C.
To solve this problem, you can use C° that describes a difference celsius:
1 °C + 1 C° = 274 K + 1 K = 275 K = 2 °C.
C° is an alias for Kelvin, thus a coherent unit too.
History
- 1.1 Some updates
- 1.0 Initial release
Presently I am a student of computer science at the Karlsruhe Institute of Technology in Germany.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 









 I have implemented simple structure UnitDouble and all works fine
I have implemented simple structure UnitDouble and all works fine