The download files contain a Visual Studio 2012 project and source files, but no executable file. If you don't use Visual Studio, or if you've another version and if the project doesn't load, then try to open Program.cs (C#) or Program.vb (VB.NET). The download file contains examples of FlagsAttribute, XOR encryption, the XOR swap algorithm ... The Main method is empty.
Table of Contents
In this article, I tell you how bitwise operators work.
All operators in this article:
- OR (Inclusive OR) (
| sign in C#, Or in VB.NET ) - AND (
& sign in C#, And in VB.NET ) - XOR (Exclusive OR) (
^ sign in C#, Xor in VB.NET) - NOT (
~ sign in C#, Not in VB.NET) - Left Shift (
<< sign in C# and VB.NET) - Right Shift (
>> sign in C# and VB.NET) - Circular Shift
- Circular Left Shift (no operator in C# and VB.NET)
- Circular Right Shift (no operator in C# and VB.NET)
Bitwise operators are used for numbers. Bitwise operators perform an action on the bits of a number, so if you want to understand how bitwise operators work, then you should first learn to convert from decimal to binary and from binary to decimal. I tell you how to do that in Converting from decimal to binary and from binary to decimal. In this article, I give examples mostly with Bytes. But the examples will also work for other types, such as an Int32 or an Int16
Bitwise operators are used in more languages than C# and VB.NET, but in this article, I give examples in C# and VB.NET.
If you use a bitwise operator, there will be an action performed for each bit in the binary form of the integer. For example 110100112 is 21110 (the subscript numbers indicate the base of the number). And 14310 is 100011112. In this paragraph, I tell how to convert from decimal to binary and how to convert from binary to decimal.
If we have a decimal number, 783 for example, then we convert it to a binary number using this way:
| Division: | 783 / 2 | 391 / 2 | 195 / 2 | 97 / 2 | 48 / 2 | 24 / 2 | 12 / 2 | 6 / 2 | 3 / 2 | 1 / 2 |
| Quotient: | 391 | 195 | 97 | 48 | 24 | 12 | 6 | 3 | 1 | 0 |
| Remainder: | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
You have to stop dividing if the quotient is 0.
Now, read the sequence of remainders from right to left, then you get the binary number 1100001111
Step-by-step explanation on converting 78310 to a binary number:
- Divide 783 by 2.
- The quotient is 391, the remainder is 1.
- Write the remainder: 1.
- Divide 391 by 2.
- The quotient is 195, the remainder is 1.
- Write the remainder: 1
- Divide 195 by 2
- The quotient is 97, the remainder is 1.
- Write the remainder: 1
- Divide 97 by 2
- The quotient is 48, the remainder is 1.
- Write the remainder: 1.
- Divide 48 by 2.
- The quotient is 24, the remainder is 0.
- Write the remainder: 0.
- Divide 24 by 2.
- The quotient is 12, the remainder is 0.
- Write the remainder: 0.
- Divide 12 by 2.
- The quotient is 6, the remainder is 0.
- Write the remainder: 0.
- Divide 6 by 2.
- The quotient is 3, the remainder is 0.
- Write the remainder: 0.
- Divide 3 by 2.
- The quotient is 1, the remainder is 1.
- Write the remainder: 1.
- Divide 1 by 2.
- The quotient is 0, the remainder is 1.
- Write the remainder: 1.
- Now, stop with dividing, because the quotient is 0.
- Read the sequence of remainders (1111000011) from right to left, then you read 1100001111. So, 11000011112 is 78310.
- Now, you can add/remove leading zeros. If your data type is a Int16, you need 16 bits. If you data type is an Int32, you need 32 bits. 783 is a Int16, so we add leading zeros until there're 16 bits: 0000001100001111.
To convert a negative decimal number to binary (-783 for example):
- Take the binary form of 783: 0000001100001111.
- Invert it: 1111110011110000
- Add up 1111110011110000 with 1.
- So, -78310 is 11111100111100012
- How you can be sure this number is negative? It depends on the data type. If the data type is an Int16, then if the first bit is a 0, then the number is positive. If the first bit is a 1, the number is negative. So, 1111110011110000 (Int16) is -783, but for an unsigned number,
UInt16 for example, the first number DOESN'T tell whether the number is negative or not. For an UInt16 for example, we can be sure it's positive because it's unsigned. So, 1111110011110000 as an UInt16 is 64752.
If you've a binary number 0000000100010110 (Int16 -> first number = 0, positive number), then reverse the order of the bits (then you get 0110100010000000), and use this method:
| Bit b: | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| b * 2n | 0 * 20 | 1 * 21 | 1 * 22 | 0 * 23 | 1 * 24 | 0 * 25 | 0 * 26 | 0 * 27 | 1 * 28 | 0 * 29 | 0 * 210 | 0 * 211 | 0 * 212 | 0 * 213 | 0 * 214 | 0 * 215 |
| Result: | 0 | 2 | 4 | 0 | 16 | 0 | 0 | 0 | 256 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Now, you have to add up all results:
0 + 2 + 4 + 16 + 0 + 0 + 0 + 256 + 0 + 0 + 0 + 0 + 0 + 0 + 0 = 2 + 4 + 16 + 256 = 278
Step-by-step explanation on converting 00000001000101102 to a decimal number:
- Reverse the order of the bits in the binary number (also change the position of the first 0 (positive sign)): 0000000100010110 -> 0110100010000000.
- Take the first bit (of 0110100010000000): 0.
- 0 * 20 is 0, so write 0
- Take the next bit: 1
- 1 * 21 is 2, so write 2
- Take the next bit: 1
- 1 * 22 is 4, so write 4
- Take the next bit: 0
- 0 * 23 is 0, so write 0
- Take the next bit: 1
- 1 * 24 is 16, so write 16
- Take the next bit: 0
- 0 * 25 is 0, so write 0
- Take the next bit: 0
- 0 * 26 is 0, so write 0
- Take the next bit: 0
- 0 * 27 is 0, so write 0
- Take the next bit: 1
- 1 * 28 is 256, so write 256
- Take the next bit: 0
- 0 * 29 is 0, so write 0
- Take the next bit: 0
- 0 * 210 is 0, so write 0
- Take the next bit: 0
- 0 * 211 is 0, so write 0
- Take the next bit: 0
- 0 * 212 is 0, so write 0
- Take the next bit: 0
- 0 * 213 is 0, so write 0
- Take the next bit: 0
- 0 * 214 is 0, so write 0
- Take the next bit: 0
- 0 * 215 is 0, so write 0
- That was the last bit, now add up all numbers you've written: 0 + 2 + 4 + 0 + 16 + 0 + 0 + 0 + 256 + 0 = 2 + 4 + 16 + 256 = 278, so 1000101102 is 27810.
The way to convert a negative binary number to decimal (1111111111010011 = Int16 -> first bit = 1, so negative):
- Invert the binary number: (1111111111010011 -> 0000000000101100)
- Convert 0000000000101100 to a decimal number: 44
- Add 44 up with 1: 45
- Make 45 negative: -45
- So, the negative binary number 1111111111010011 is the decimal number -45
If you've two numbers, 38 (Byte) and 53 (Byte) for example, then first we convert these numbers to binary:
38 -> 00100110
53 -> 00110101
- Now, we take the first bit of 38 (A), and the first bit of 53 (B). A = 0 and B = 0
- If A is 1, B is 1 or if they're both 1, then write 1. If they're both 0, then write 0.
- A and B are both 0, so write 0
- Take the next bits. Now, A = 0 and B = 0
- A and B are both 0, so write 0
- Take the next bits. Now, A = 1 and B = 1
- A and B are both 1, so write 1
- Take the next bits. Now, A = 0 and B = 1
- A is 0, but B is 1, so write 1
- Take the next bits. Now, A = 0 and B = 0
- A and B are both 0, so write 0
- Take the next bits. Now, A = 1 and B = 1
- A and B are both 1, so write 1
- Take the next bits. Now, A = 1 and B = 0
- B is 0, but A is 1, so write 1
- Take the next bits. Now, A = 0 and B = 1
- A is 0, but B is 1, so write 1
- This is the sequence of all written numbers: 00110111
- If you convert 00110111 to a decimal number, then you get 55. So,
38 | 53 (38 Or 53 in VB.NET) is 55
Corresponding table of this method:
| A | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| B | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| A | B (A Or B) | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
If one of the two numbers is a Int16 for example, then one of the two numbers may be negative. If the sign of the first Int16 is 0 (positive), and the sign of the second number is 1 (negative), then the sign in the result will be 1. So, -15 | 378 (-15 Or 378 in VB.NET) is -5.
C# and VB.NET code for an OR operator:
byte inclusiveOrExample = 38 | 53;
Dim inclusiveOrExample As Byte = 38 Or 53
You can treat an enum as a bit field using a FlagsAttribute[^]. In an enum with a FlagsAttribute, you should set the first value to 1, the second value to 2, the third value to 4, the fourth value to 8 ... Set "None" to 0.
[Flags]
public enum Priority
{
None = 0,
VeryLow = 1,
Low = 2,
Medium = 4,
High = 8,
VeryHigh = 16
}
<Flags>
Public Enum Priority
None = 0
VeryLow = 1
Low = 2
Medium = 4
High = 8
VeryHigh = 16
End Enum
Now, you can combine the enum values using the OR operator:
Priority p = Priority.Medium | Priority.High;
Console.WriteLine(p.ToString());
Dim p As Priority = Priority.Medium Or Priority.High
Console.WriteLine(p.ToString())
The output will be Medium, High because I use a FlagsAttribute. If I remove the [Flags] (<Flags> in VB.NET), then the output will be 12. Important note: if you also want to declare a value "MediumHigh", then the value "MediumHigh" should be Medium | High (Medium Or High in VB.NET).
If you've two numbers, 76 and 231 for example, then first we convert these numbers to bytes:
76 -> 01001100
231 -> 11100111
- Now, we take the first bit of 76 (A) and the first bit of 231 (B). A = 0 and B = 1
- If A and B are both 1, then write 1. Otherwise, write 0.
- A isn't 1, so write 0
- Take the next bits. Now, A = 1 and B = 1
- A and B are both 1, so write 1
- Take the next bits. Now, A = 0 and B = 1
- A isn't 1, so write 0
- Take the next bits. Now, A = 0 and B = 0
- A and B are both 0, so write 0
- Take the next bits. Now, A = 1 and B = 0
- B isn't 1, so write 0
- Take the next bits. Now, A = 1 and B = 1
- A and B are both 1, so write 1
- Take the next bits. Now, A = 0 and B = 1
- A isn't 1, so write 0
- Take the next bits. Now, A = 0 and B = 1
- A isn't 1, so write 0
- This is the sequence of all written bits: 01000100
- Convert 01000100 to a decimal number: 68
- So,
76 & 231 (76 And 231 in VB.NET) is 68
Corresponding table of this method:
| A | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| B | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| A & B (A And B) | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
A & B (A And B in VB.NET) will be negative if A and B are both negative, otherwise, A & B (A And B) will be positive.
C# and VB.NET implementation of the AND operator:
byte andOperatorExample = 76 & 231;
Dim andOperatorExample As Byte = 76 And 231
The Exclusive OR operator is not the same as the Inclusive OR operator. If you use an Inclusive OR, 1 | 1 (1 Or 1 in VB.NET) is 1. But if you use an XOR operator, 1 ^ 1 (1 Xor 1 in VB.NET) is not 1, but 0. Only 0 ^ 1 (0 Xor 1 in VB.NET) and 1 ^ 0 (1 Xor 0 in VB.NET) return 1.
If you have two numbers, 138 and 43 for example, then use this way to calculate 138 ^ 43 (138 Xor 43 in VB.NET):
-
138 -> 10001010
43 -> 00101011
- Take the first bit of 138 (A) and the first bit of 43 (B). A = 1 and B = 0
- A is 1, B is 0, so write 1
- Take the next bits. Now, A = 0 and B = 0
- A and B are both 0, so write 0
- Take the next bits. Now, A = 0 and B = 1
- A is 0, B is 1, so write 1
- Take the next bits. Now, A = 0 and B = 0
- A and B are both 0, so write 0
- Take the next bits. Now, A = 1 and B = 1
- A and B are both 1, so write 0
- Take the next bits. Now, A = 0 and B = 0
- A and B are both 0, so write 0
- Take the next bits. Now, A = 1 and B = 1
- A and B are both 1, so write 0
- Take the next bits. Now, A = 0 and B = 1
- A is 0, B is 1, so write 1
- This is the sequence of all written bits: 10100001
- Convert 10100001 to a decimal number, then you get 161
- So,
138 ^ 43 (138 Xor 43 in VB.NET) is 161
Corresponding table of this method:
| A | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| B | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| A ^ B (A Xor B) | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
C# and VB.NET implementation of the Exclusive OR (XOR) operator:
byte exclusiveOrExample = 138 ^ 43
Dim exclusiveOrExample As Byte = 138 Xor 43
With the XOR swap algorithm[^], you can swap the values of two variables (having the same data type) without using a temporary variable.
int x = 31643;
int y = 134;
x ^= y;
y ^= x;
x ^= y;
Console.WriteLine(x);
Console.WriteLine(y);
Dim x As Integer = 31643
Dim y As Integer = 134
x = x Xor y
y = x Xor y
x = x Xor y
Console.WriteLine(x)
Console.WriteLine(y)
With the XOR operator, you can encrypt some text. Iterate over all characters, and the new (encrypted) character is c ^ k (c Xor k in VB.NET). c is the int value of the current char, k is the int value of a key.
string msg = "This is a message.";
char k = '.';
StringBuilder sb = new StringBuilder();
foreach (char c in msg)
{
sb.Append((char)(c ^ k));
}
Console.WriteLine(sb.ToString());
Dim msg As String = "This is a message."
Dim k As Char = "."C
Dim sb As New StringBuilder()
For Each c As Char In msg
sb.Append(ChrW(AscW(c) Xor AscW(k)))
Next
Console.WriteLine(sb.ToString())
The output is zFG]♫G]♫O♫CK]]OIK. This is simple to break using frequency analysis[^]. So, don't use one char as a key, but a string:
string msg = "This is a message.";
string k = "97k/ -X.O";
StringBuilder sb = new StringBuilder();
for (int i = 0; i < msg.Length; i++)
{
sb.Append((char)(msg[i] ^ k[i % k.Length]));
}
Console.WriteLine(sb.ToString());
Dim msg As String = "This is a message"
Dim k as String = "97k/ -X.O"
Dim sb As New System.Text.StringBuilder()
For i As Integer = 0 To msg.Length - 1
sb.Append(ChrW(AscW(msg(i)) Xor AscW(k(i Mod k.Length))))
Next
Console.WriteLine(sb.ToString())
The output is m_☻\ D+♫.↓Z♫\SL?Ka. Now, you can't break this using frequency analysis. But your application can be decompiled and if someone knows the key, then it's easy to decrypt your message. So, don't use only XOR encryption to encrypt a message. Anyway, if you're interested in security and encryption, you can use XOR encryption as a part of your encryption algorithm.
The bitwise NOT operator inverts each bit in a sequence of bits. A 0 becomes a 1, and a 1 becomes a 0. If the data type is a signed data type, a positive number becomes a negative number, and a negative number becomes a positive number. If the data type is a unsigned data type, a positive number stays positive. If you've a number, 52 for example (00110100 in binary, and a Byte, unsigned data type, so it's positive), then calculate ~52 (Not 52 in VB.NET) using this way:
| A | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| ~A | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
Convert 11001011 to a decimal number, then you get 203. So, ~52 (as a Byte) is 203.
The NOT operator in C# and VB.NET:
byte b = 52;
byte notB = (byte)~b;
Int16 int16NotB = (Int16)~b;
Dim b As Byte = 52
Dim notB As Byte = Not b
Dim int16NotB As Int16 = CShort(Not b)
In C#, if you convert ~b to a short (Int16), then you get -53. But if you convert Not b to an Int16 in VB.NET, then you get 203. Why? I tried (~b).GetType() in C#, and I got System.Int32. I tried (Not b).GetType() in VB.NET, and I got System.Byte. So, the standard data type of an inversed byte is Int32 in C#, and Byte in VB.NET. In this table, I calculate (Int16)~52:
| A | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| ~A (Not A) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
Convert 1111111111001011 to a decimal number (Int16 = signed data type, first bit is 1, so negative), and the result is -53. So, (Int16)~52 is -53.
x << n (a Left Shift) shifts all bits in x n places to left, and the empty bit-positions are filled with zeros.
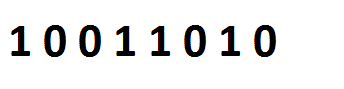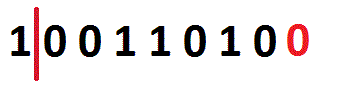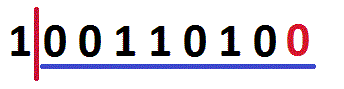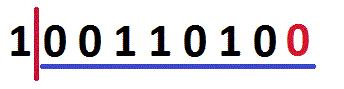
As you can see on the image, all bits are moved one place to left, and the empty bit-position is filled with a zero. So, 154 << 1 is 52.
5 << 2 shifts all bits in the binary form of 5 (00000101) two places to left: 00010100 (binary form of 2010). So, 5 << 2 is 20. A table on calculating 154 << n:
| 154 << 0 (= 154) | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 154 << 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 154 << 2 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| 154 << 3 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 154 << 4 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 154 << 5 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 154 << 6 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 154 << 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 154 << 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
The Left Shift operator in C# and VB.NET:
byte b1 = 154;
byte b2 = (byte)(b1 << 1);
Console.WriteLine(b2);
Dim b1 As Byte = 154
Dim b2 As Byte = b1 << 1
Console.WriteLine(b2)
1 << n returns 2<sup>n</sup>, but calculating powers of 2 using the Left Shift is faster than using the Math.Pow method:
System.Diagnostics.Stopwatch sw = new System.Diagnostics.Stopwatch();
sw.Start();
byte pow = 1 << 7;
sw.Stop();
Console.WriteLine(sw.Elapsed.TotalMilliseconds);
sw.Reset();
sw.Start();
byte mathPow = (byte)Math.Pow(2, 7);
sw.Stop();
Console.WriteLine(sw.Elapsed.TotalMilliseconds);
Dim sw As New System.Diagnostics.Stopwatch()
sw.Start()
Dim pow As Byte = 1 << 7
sw.[Stop]()
Console.WriteLine(sw.Elapsed.TotalMilliseconds)
sw.Reset()
sw.Start()
Dim mathPow As Byte = CByte(Math.Pow(2, 7))
sw.[Stop]()
Console.WriteLine(sw.Elapsed.TotalMilliseconds)
x >> n (a Right Shift) shifts all bits in x n places to right, and the empty bit-positions are filled with zeros.
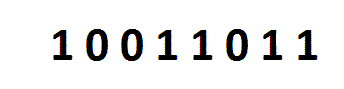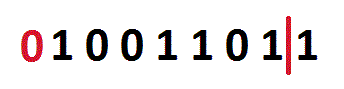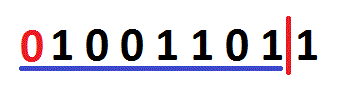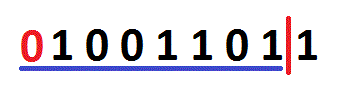
As you can see on the image, all bits are moved one place to right, and the empty bit-position is filled with a zero. So, 155 >> 1 is 77. Important note: if you've a signed data type, then the sign will be preserved.
A table on calculating 155 >> n:
| 155 >> 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 155 >> 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 155 >> 2 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| 155 >> 3 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 155 >> 4 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 155 >> 5 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 155 >> 6 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 155 >> 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 155 >> 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
The Right Shift operator in C# and VB.NET:
byte b1 = 155;
byte b2 = (byte)(b1 >> 1);
Console.WriteLine(b2);
Dim b1 As Byte = 155
Dim b2 As Byte = b1 >> 1
Console.WriteLine(b2)
x >> n is equal to x / 2<sup>n</sup>. For example, 8 >> 2 is equal to 8 / 2<sup>2</sup> and that is equal to 8 / 4 and that is equal to 2. So, 8 >> 2 is 2.
byte b = (byte)(8 >> 2);
Console.WriteLine(b);
Dim b As Byte = 8 >> 2
Console.WriteLine(b)
This is also faster than 8 / Math.Pow(2, 2);
System.Diagnostics.Stopwatch sw = new System.Diagnostics.Stopwatch();
sw.Start();
byte divisionUsingRightShift = 8 >> 2;
sw.Stop();
Console.WriteLine(sw.Elapsed.TotalMilliseconds);
sw.Reset();
sw.Start();
byte divisionUsingMathPow = (byte)(8 / Math.Pow(2, 2));
sw.Stop();
Console.WriteLine(sw.Elapsed.TotalMilliseconds);
Dim sw As New System.Diagnostics.Stopwatch()
sw.Start()
Dim divisionUsingRightShift As Byte = 8 >> 2
sw.[Stop]()
Console.WriteLine(sw.Elapsed.TotalMilliseconds)
sw.Reset()
sw.Start()
Dim divisionUsingMathPow As Byte = CByte(8 / Math.Pow(2, 2))
sw.[Stop]()
Console.WriteLine(sw.Elapsed.TotalMilliseconds)
A Circular Left Shift shifts all bits in b n places to left, and fills the last bit with the first bit (of the byte before shifting). 
The image shows 154 circularleftshift 1. 154 circularleftshift 1 is (for a byte) equal to 154 << 1 | 154 >> 7, and a circularleftshift n is equal to a << n | a >> (b - n). b is the count of bits. So, for a byte, the formula is a << n | a >> (8 - n), and for an Int32, the formula is a << n | a >> (32 - n). The circular left shift in C# and VB.NET (for a byte):
static byte CircularLeftShift(byte a, byte n)
{
return (byte)(a << n | a >> (8 - n));
}
byte b1 = CircularLeftShift(154, 1);
byte b2 = CircularLeftShift(154, 2);
Private Function CircularLeftShift(a As Byte, n As Byte) As Byte
Return CByte(a << n Or a >> (8 - n))
End Function
Dim b1 As Byte = CircularLeftShift(154, 1)
Dim b2 As Byte = CircularLeftShift(154, 2)
A Circular Right Shift shifts all bits in b n places to right, and fills the first bit with the last bit (of the byte before shifting).
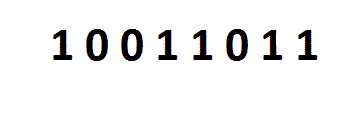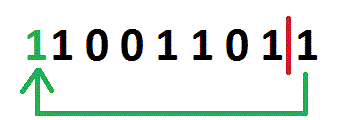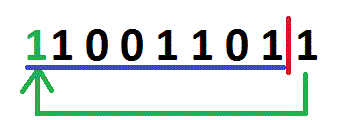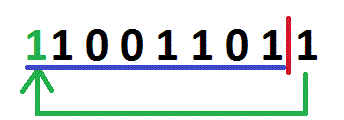
The image shows 155 circularrightshift 1. 155 circularrightshift 1 is (for a byte) equal to 155 >> 1 | 154 << 7, and a circularrightshift n is equal to a >> n | a << (b - n). b is the count of bits. So, for a byte, the formula is a >> n | a << (8 - n), and for an Int32, the formula is a >> n | a << (32 - n). The circular right shift in C# and VB.NET (for a byte):
static byte CircularRightShift(byte a, byte n)
{
return (byte)(a >> n | a << (8 - n));
}
byte b1 = CircularRightShift(155, 1);
byte b2 = CircularRightShift(155, 2);
Private Function CircularRightShift(a As Byte, n As Byte) As Byte
Return CByte(a >> n Or a << (8 - n))
End Function
Dim b1 As Byte = CircularRightShift(155, 1)
Dim b2 As Byte = CircularRightShift(155, 2)
- 30 Mar 2013
- Download added
- 27 Mar 2013
- Changed Calculating x / 22 using the Right Shift operator into Calculating x / 2n using the Right Shift operator
- 18 Mar 2013
- Circular Shift added
- 12 Mar 2013
- Minor error[^] fixed, Table of Contents added
- 9 Mar 2013
- I changed the description of the Left Shift and the Right Shift (Andreas Gieriet corrected me in this message[^])
- 8 Mar 2013
- First version
This member has not yet provided a Biography. Assume it's interesting and varied, and probably something to do with programming.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin