Abstract
In this article, .NET parallel class is utilized to boost the performance of bi-conjugate gradient stabilized algorithm which is an iterative method of solving system of linear equations. A Matrix class with appropriate operators, methods and properties is developed. A solver class capable of performing the algorithm on separate thread is developed and, a set of matrices of size 1000, 1500, 2000, 2500, 3000, 4000 and 6000 is tested and discussed. In this study, implementing Parallel Class could reduce the CPU time by an average of 41% and maximum of 65%.
Introduction
.NET Framework Parallel Class provides developers with a simple structured loop that executes a block in parallel on several cores. This class was first introduced with .NET Framework 4.0 and since then, it’s been practiced in several studies. In this article, Parallel Class is implemented inside a globally experienced algorithm of solving a system of linear equations known as bi-conjugate gradient stabilized. This job is performed through splitting the independent computations and performing them on iterations of the parallel loop. As for any equation of this type, the input data includes matrices of A, X and b. Matrices of X and b are in size n while matrix of A is of size n^2 . Thus, matrix of A requires heavy computations and it can be considered as a target of parallel computation wherever it appears inside the algorithm.
Bi-Conjugate Gradient Stabilized
Bi-Conjugate Gradient Stabilized or briefly BiConGradStab is an advanced iterative method of solving system of linear equations. This method and other methods of this family such as Conjugate Gradient are perfect for memory management due to implementing vectors of size n in their calculations rather than matrices of size n^2. In addition, this method is not restricted to a specific type or size of matrix and can be applied to any sparse matrices of A. The following illustrates the algorithm of BiConGradStab method.
- r0 = b − Ax0
- Choose an arbitrary vector r̂0 such that (r̂0, r0) ≠ 0, e.g., r̂0 = r0
- ρ0 = α = ω0 = 1
- v0 = p0 = 0
- For i = 1, 2, 3, …
- ρi = (r̂0, ri−1)
- β = (ρi/ρi−1)(α/ωi−1)
- pi = ri−1 + β(pi−1 − ωi−1vi−1)
- vi = Api
- α = ρi/(r̂0, vi)
- s = ri−1 − αvi
- t = As
- ωi = (t, s)/(t, t)
- xi = xi−1 + αpi + ωis
- If xi is accurate enough then quit
- ri = s − ωit
As shown above, there are two steps of 4 and 7 involved with matrices of size n^2 where matrices can be divided into smaller ones and then computed separately in parallel processes.
Matrix Class
In order to perform clear and easy-to-understand matrix calculations, it’s necessary to develop a matrix class that complies with algorithms and calculations. Following lists some of the properties, methods and operators of the developed matrix class.
| Property | Description |
n (Integer) | Returns number of i elements |
m (Integer) | Returns number of j elements |
Values (Double(,)) | (Default property) gets or sets values of element at i and j |
| Method | Description |
New () | Overloads: 1.void, 2. gets size of matrix, 3. returns identity matrix 4. gets values. |
T() | Returns transposed of calling matrix |
Split() | Splits current matrix into matrices of same n and returns an array of them |
Join() | Joins matrices of same n and returns a matrix |
CopyTo() | Copies elements in current matrix onto another matrix |
| Operator | Description |
| -/+ | Subtracts/adds matrices of appropriate size |
| * | Multiplies matrices of appropriate size |
| / | Divides element at (0,0) of one matrix by element of the same at another matrix and returns a matrix of size 1*1 of the result. |
Solver Class
The Solver Class contains methods and event for performing the BiConGradStab calculations. The SolverThread is executed in a separate class of SolverThreadClass. The Solve() method requires matrices of A, b, initial guess for X, number of parallel processes nParallel, and final iteration Iteration.
Public Sub Solve(A As Matrix, X As Matrix, b As Matrix, Parallel As Integer, Iterations As Integer)
A.CopyTo(Me.A)
X.CopyTo(Me.X)
b.CopyTo(Me.b)
SolverThread = New SolverThreadClass
AddHandler SolverThread.Solved, AddressOf _Solved
Dim T As New Threading.Thread(New Threading.ParameterizedThreadStart_
(AddressOf SolverThread.SolverThread))
T.Start(New Object() {_A, _X, _b, Parallel, Iterations})
End Sub
In Solve() method of the SolverThreadClass, the matrices of A and b are split into nParallel number of smaller matrices using Split() method.
Dim A() As Matrix = rawA.Split(nParallel)
Dim b() As Matrix = rawB.Split(nParallel)
In the main loop as shown below, steps 4 and 7 of the algorithm are being executed in Parallel blocks.
Do While nIteration < Iterations
NewRho = r_tilde * r
beta = (NewRho / Rho) * (Alpha / Omega)
P = r + beta * (P - Omega * V)
Parallel.For(0, nParallel, Sub(i As Integer)
V_Split(i) = A(i) * P
End Sub)
V.Join(V_Split)
Alpha = NewRho / (r_tilde * V)
s = r - Alpha * V
Parallel.For(0, nParallel, Sub(i As Integer)
t_Split(i) = A(i) * s
End Sub)
t.Join(t_Split)
Omega = (t.T * s) / (t.T * t)
X += Alpha * P + Omega * s
r = s - Omega * t
NewRho.CopyTo(Rho)
nIteration += 1
Loop
Using the Code
In order to use this solver in your application, you need to declare it as below so that you would be able to catch the Solved event once it's fired.
Friend WithEvents mySolver As Solver
And Solved event handler can be written as below:
Sub Solved(X As Matrix) Handles mySolver.Solved
Stop
End Sub
Now in the calling procedure, the solver class is instantiated and called for matrices of system of linear equations. A simple example is given:
mySolver = New Solver
Dim A As New Matrix(3, 3)
Dim x As New Matrix(1, 3)
Dim b As New Matrix(1, 3)
A(0, 0) = 0.1
A(1, 1) = 0.4
A(2, 2) = 0.2
A(1, 0) = 0.45
A(0, 1) = 0.67
A(0, 2) = 0.98
b(0, 0) = 1
b(0, 1) = 1.47
b(0, 2) = 1.58
x(0, 0) = 4
x(0, 1) = 2
x(0, 2) = 1
mySolver.Solve(A, x, b, 1, 5)
Results
CPU: 2.8GHz and | RAM: 2GB | Precision: Double
Matrix Size: 1000*1000
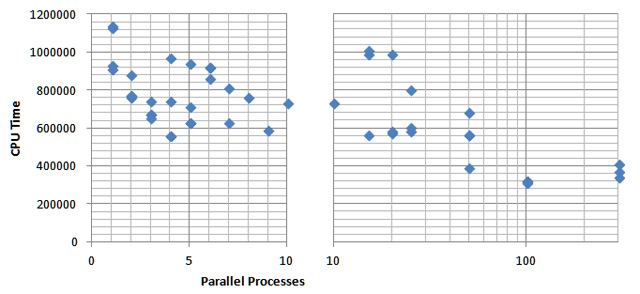
Matrix Size: 2000*2000

Matrix Size: 4000*4000
Matrix Size: 6000*6000
Discussion
The average CPU Time graph is a good indicator of the overall performance of Parallel Class for each matrix. As shown in the graph, the CPU time decreases gradually as the size of matrix increases relatively. For matrix of size 6000, it can be interpreted as a memory access issue as matrix of size 6000 would take two times more memory than that of 4000. In addition, the graph of best CPU Times suggests that the performance of Parallel Class for BiConGradStab gets improved softly by increasing the size of the matrix.

Conclusions
- The Parallel class improves the performance of
BiConGradStab by 41 to 65% on multi-runs and -35% to 75% on single-runs of CPU time on a dual core 2.8GHz with 2GB of RAM having Windows 8.1 installed and continuous condition. This may be relatively different on other systems of different hardware and software capabilities. - With high level of certainty, one would try using Parallel class for matrices of size 1000 and more and expect significant improvement in overall performance.
- There’s no exact estimation of improvement in overall or local performance because it’s being affected by several factors. But as for higher number of parallel processes, we’ve got least fluctuation and Parallel gives more reliable result.
- Best results achieved at maximum parallel processes where Iterations on Parallel class are comparable to size of the matrix, e.g., 1000 Parallel processes for a matrix of 3000 on each side.
- For smaller matrices, Parallel class is unstable but still effective.
Recommendations
- For more serious work, it'd be better to add tolerance and/or mse checkers to the iterative part of the code.
- Using pre-conditioners, one would achieve better convergence speed for
BiConGradStab method. Nonetheless, this code does not aim at evaluating the accuracy or convergence speed of this method. - A memory and CPU check procedure can be developed so that user would get informed about the status of memory and CPU before and when the iterations are in progress.
- At many scenarios, users may need to perform the algorithm several times for simulation purposes. For such cases, that would be great if a survey method determines the best run structure prior to the simulation job.
- The whole work could be simply accomplished through two separated loops of matrix operations without having other parts of
BiConGradStab algorithm involved, this work aims at showing the practical aspect of Parallel Class. One would try similar code for other iterative solutions wherever Parallel computation is possible.
I'm a Full-stack Software Developer with over a decade of experience at industrial and research projects having my main focus on Microsoft .Net stack.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 






