In this puzzle, we’re going to learn how to find the person whose birthday, among others, is in the middle. Knowing how to calculate the median value is a good skill to have. As you start to explore business intelligence, you’ll come across similar problems to solve.
Also, be sure to check out the bonus question. We’ll work with date from colonial times. The calendar was different, and you see that the standard DATETIME datatype falls short of our challenge.
Solving puzzles is a great way to learn SQL. Nothing beats practicing what you’ve learned. Once you have figured out the puzzle, post your answer in the comments so we can all learn from one another.
Calculate the Median Date among a List of Dates
Here is today’s puzzle written by Chris Huntley.
You have a list of people with birth dates and want to find the person who has the middle birth date?
In other words, who has the median birth date?
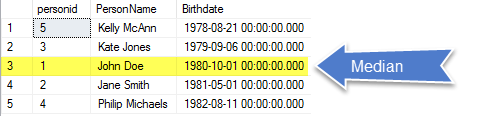
Are you up to the challenge? Can you write a single SQL statement to find this person?
To get started, be sure to download the code samples. You’ll find sample data for this and the bonus question here.
Beware of Date Conversion Issues
The first idea might be to convert it to an integer and then use that in a sort or to calculate median values. However, depending on how you convert it, you may end up with something you don’t want. For example, converting it to a numeric looking string and then into an integer value.
Here is one way to convert date to an INT, but not the right way!
SELECT personid,
personname,
birthdate,
CAST(CONVERT(NVARCHAR(10), birthdate,112)as INT) as BirthINT,
CAST(CONVERT(NVARCHAR(10), birthdate,112)as INT)+1 as BirthINTIncremented,
CAST(CONVERT(NVARCHAR(10), birthdate,112)as INT)+30 as BirthINTIncrementedMore
FROM @datetable
A disadvantage of this conversion is shown below. You can increment it like any other integer but it isn’t a date anymore so you get dates that don’t really exist. Incrementing dates should be done with appropriate datatypes and possibly appropriate functions.

Continuing with this idea, we just calculate the median value of this integer and get the following:
;WITH ctedateconversion AS (
SELECT personid,
personname,
birthdate,
CONVERT( INT, Birthdate) as BirthINT
FROM @datetable
)
SELECT CONVERT(DATETIME,
SUM(birthint)/(SELECT COUNT(*) FROM cteDateconversion)) As meanbirthdate
FROM ctedateconversion

We do get the median date, but it’s not a date on our list meaning it doesn’t represent a person in our table.
If we remove the outside conversion back into a date...
SUM(birthint)/(SELECT COUNT(*) FROM cteDateconversion) As meanbirthdate
...we would have received the value 29438.
Which is the number of days since 1/1/1900.
If you want to confirm this, use the following code:
SELECT DATEDIFF(dd, '1900-01-01 00:00:00','1980-08-07 00:00:00.000')
Answer to Calculating the Median Date
To get the median birth date, I decided to use (2) PERCENTILE_DISC. PERCENTILE_DISC computes a specific percentile for a distribution, which in our example, is a list of dates. Specifying PERCENTILE_DISC (.5) calculates the 50th percentile, which happens to be the median.
;with ctedateconversion as(
SELECT personid,
PersonName,
Birthdate,
Percentile_Disc(0.5) within group (order by Birthdate) OVER() as MedianBirthDate
FROM @datetable
)
SELECT personname,
birthdate
FROM ctedateconversion
WHERE Birthdate = MedianBirthDate
This gives us the answer:

There’s more than one way to get the answer you seek. How did you accomplish this task?
Bonus Question
Find the specific presidents that were the mean age of all presidents when they entered or left the presidency. Specifically, either they were the mean age of all presidents when they entered or the mean age of all presidents when they left. This requires you consider the datatypes you use carefully. The analyst who collected this data for you gave it to you in a denormalized format with everything in a string datatype since they couldn’t get DATETIME to work.
To get started, be sure to download the code samples. You’ll find sample data for the bonus question here.
Sample Data
The first thought might be convert it to a DATETIME, then just do the math. If you try that, you’ll find an error.
SELECT President,
Convert(DATETIME, Birthdate) as Birthdate,
Convert(DATETIME, TermStart) TermStart,
Convert(DATETIME, TermEnd) as TermEnd
FROM Presidents
Why?

DATETIME has a history and the dates it can hold are limited to dates greater than 1/1/1753. The history is that Pope Gregory, for whom the calendar is named, in 1582 enacted reform to change from the Julian to Gregorian calendar.
It took Britain and the Colonies quite a while to get around to it and they finally decided that 1752 would be the change over. In order to make the change over, they had to drop 11 days from September 1752.
Way back, when they were designing SQL server, they chose to just ignore this period and support from 1753 onward using the Gregorian Calendar.
An option might be convert to DATETIME2 which is Gregorian and supports all dates down to 00/00/0001 which makes it compatible with other DBMS.
SELECT President,
Convert(DATETIME2, Birthdate) as Birthdate,
Convert(DATETIME2, TermStart) TermStart,
Convert(DATETIME2, TermEnd) as TermEnd
FROM Presidents
How do we want to get this data? We can use chained CTEs (Common Table Expression) so we can convert and then perform the calculations as follows:
; with ctepresidents as(
SELECT President,
Convert(DATETIME2, Birthdate) as Birthdate,
Convert(DATETIME2, TermStart) TermStart,
Convert(DATETIME2, TermEnd) as TermEnd
FROM Presidents
)
,
CTESTEP2 as(
SELECT President,
CAST(DATEDIFF(dd, birthdate, termstart)/365.0 as INT) as startage,
CAST(DATEDIFF(dd, birthdate, termend)/365.0 as INT) as endage
FROM ctepresidents
)
,ctefinal as(
SELECT CAST(SUM(startage)/(select COUNT(*) FROM Ctestep2)as INT) as meanStartAge,
CAST(SUM(endage)/(select COUNT(*) FROM Ctestep2)as INT )as meanendAge
FROM CTESTEP2)
,cteconnectingitall as(
SELECT President
FROM CTESTEP2 c
INNER JOIN CTEFINAL f
on c.startage = f.meanStartAge
UNION ALL
SELECT President
FROM ctefinal ff
INNER JOIN CTESTEP2 cc
ON cc.endage = ff.meanendAge
)
SELECT * FROM cteconnectingitall
Giving us:
The mean age of start of a presidential term is: 54
The mean age of the end of a presidential term is: 59
Just to make confirmation easier, here’s the code:
;with ctepresidents as(
SELECT President,
Convert(DATETIME2, Birthdate) as Birthdate,
Convert(DATETIME2, TermStart) TermStart,
Convert(DATETIME2, TermEnd) as TermEnd
FROM Presidents
)
,
CTESTEP2 as(
SELECT President,
CAST(DATEDIFF(dd, birthdate, termstart)/365.0 as INT) as startage,
CAST(DATEDIFF(dd, birthdate, termend)/365.0 as INT) as endage
FROM ctepresidents
)
SELECT * FROM CTESTEP2
WHERE startage = 54
OR endage = 59

How did you get the answer? Did you have a flatter and easier way?
Bio
This blog was authored by Chris Huntley. He is a Business Intelligence Developer living in Dallas Fort Worth. He loves data, the Microsoft Bi Stack and tacos not necessarily in that order.
Chris frequently helps fellow SQL coders. One place you can find him is on the essentialSQL learning group.
Hello my name is Kris. I’m here because I am passionate about helping non-techie people to overcome their fear of learning SQL.
I know what it is like to not know where to start or whether the time spent learning is worth the effort. That is why I am here to help you to:
- Get started in an easy to follow step-by-step manner.
- Use your time wisely so you focus on what is important to learn to get the most value from your time.
- Answer your questions. Really! Just post a comment and I’ll respond. I’m here to help.
It wasn’t long ago that I was helping a colleague with some reporting. She didn’t know where to start and soon got overwhelmed and lost as she didn’t know SQL.
I felt really bad, as she was under pressure to get some summary information to her boss, the built-in reports were falling short, and to make them better would require her to know SQL. At that time that seemed impossible! It in dawned on me, it doesn’t have to be that way.
Then I discovered a way for anyone with the desire to easily learn SQL. I worked with my co-worker, started to teach her what I learned and soon she was able to write reports and answer her boss’ questions without getting stressed or ploughing hours into manipulating data in Excel.
It hasn’t always been easy. Sometimes the information seems abstract or too conceptual. In this case I’ve found out that a visual explanation is best. I really like to use diagrams or videos to explain hard-to-grasp ideas.
Having video, pictures, and text really help to reinforce the point and enable learning.
And now I want to help you get the same results.
The first step is simple, click here http://www.essentialsql.com/get-started-with-sql-server/




