The Diffie-Hellman Key Exchange algorithm, also called exponential key exchange, which is one of the public key exchange algorithm used in cryptography.
Introduction
The Diffie-Hellman Key Exchange algorithm, also called exponential key exchange, is one of the public key exchange algorithm. The algorithm is used for sharing the keys between two parties. The intruder cannot calculate the key until he cracks the private value of one of the parties.
Using the Code
The main part of the code is written in the class "DiffieHellman".
public class DiffieHellman {
BigInteger p, g;
public DiffieHellman(){}
public void genPrimeAndPrimitiveRoot(){
this.p = BigInteger.valueOf(new PrimeNumberGen().getPrimeNumber());
this.g = BigInteger.valueOf(new PrimitiveRootGen(this.p.intValue()).getPr());
}
public BigInteger getP() {
return p;
}
public BigInteger getG() {
return g;
}
public BigInteger getAliceMessage(BigInteger aliceSecretNumber){
return this.g.modPow(aliceSecretNumber, this.p);
}
public BigInteger getBobMessage(BigInteger bobSecretNumber){
return this.g.modPow(bobSecretNumber, this.p);
}
public BigInteger aliceCalculationOfKey
(BigInteger bobMessage, BigInteger aliceSecretNumber){
return bobMessage.modPow(aliceSecretNumber, this.p);
}
public BigInteger bobCalculationOfKey
(BigInteger aliceMessage, BigInteger bobSecretNumber){
return aliceMessage.modPow(bobSecretNumber, this.p);
}
}
The algorithm starts with calculating two values "p" and "g", which are public values shared by both users. The "p" is prime number, and "g" is one of the primitive root of "p".
The second step of the algorithm is selecting private values. Assumes the names of parties who are going to share the code are "Alice" and "Bob". Alice selects her secret key as aliceSec and Bob selects his secret key as bobSec.
The third step of the algorithm calculates the message to be shared between parties. Alice calculates her message by:
aliceMsg = galiceSec % p
And Bob calculates his message by:
bobMsg = gbobSec % p
Then, Alice and Bob will share the keys between them.
The next and last step is calculation of key. Alice calculates key from her end by using the formula:
aliceKey = bobMsgaliceSec % p
And Bob calculates key from his end using the formula:
bobKey = aliceMsgbobSec % p
The keys calculated by Alice and Bob will be equal and the key cannot be calculated (crack) by third party until he/she knows the secret key of Alice or Bob. Until the secret key is kept as secret, the key will be secured. :)
Screenshot
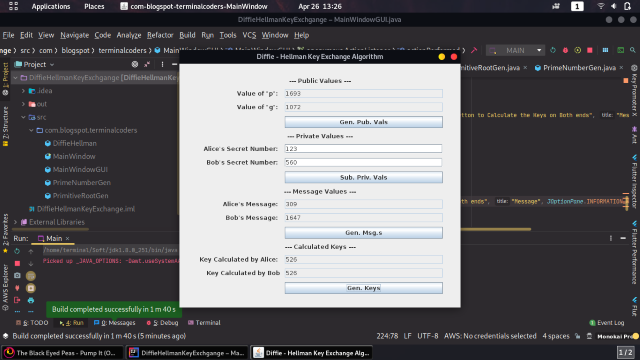
Points of Interest
It is interesting to see how the Euclidean algorithms are useful in network security and cryptography.
History
- 26th April, 2020: Initial version
Name Ajith Kp. Currently working at Tata Consultancy Service Ltd. I completed MCA from School of Information Science and Techonolgy, Kannur University Campus, Mangattuparamba. I like programming as well as computer/network security analyzing. I'm concentrating programming in Android, PHP, Python, Ajax, JQuery, C# and JAVA.
Blog: http://www.terminalcoders.blogspot.com
Knowledge in Java, Python, PHP, and Android.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 








