| 
fig. 1 - one normal per triangle
| 
fig. 2 - interpolated normals
|
| 
fig. 3 - testing with reflective material
|
Introduction
In this new article in our ray-tracing series we will start handling more complex objects. These objects are formed by points, vertices and polygons as we have seen before.
Polygons as flat surfaces have one normal vector, and this vector against the light vectors and viewer vector gives us its color. So, working with one normal per polygon face gives a non linear result as we see in fig. 1. To solve this I have implemented an algorithm to obtain normals at each vertex and them for each ray hitpoint provide a normal interpolation between the triangle vertices giving us different normals on each polygon intersection, and hence a linear colouring between the vertices.
Note: All the articles I am posting here are for learning purposes, so do not worry at any point about speed or optimization. Instead we will keep that for more advanced articles, so please do not focus on improvements at this point.
Background
At first I recommend a previous reading in the last ray tracing articles.
Calculating normal vector of triangles
From linear algebra a normal vector of a plane can be obtained by proceeding a cross product between two vectors of this plane.
In our situation a triangle is ideal, by definition 3 points gives us a unique plane.
We have P1, P2 and P3, it is easy to get 2 vectors from this:
a = P1-P2
b = P3-P2 (remember we have 3 coordinates for each point x,y,z)
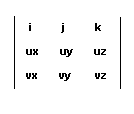
Fig 3 - cross product matrix
The cross product is given by solving the matrix given by fig. 3:
public static void Cross3(double ax, double ay, double az,
double bx, double by, double bz,
ref double outx, ref double outy, ref double outz)
{
outx = ay * bz - az * by;
outy = az * bx - ax * bz;
outz = ax * by - ay * bx;
}
At this point our rendering has the fig. 1 result. Now lets think about how to calculate the interpolated normals.
At first we need to get normals for each triangle vertex, but how to achieve this?
Once we already have one normal per triangle, obtained by cross product, lets look to our points grid.
Each point belongs to more than one triangle, so it is easy to get a normal composition for each point by just adding each triangle normal on this. Aha, now we have normals at vertices!
But it is not enough... How to interpolate a hitpoint inside a triangle if we have just the vertices normals?
It is simple, we need to calculate in a similar way as we calculated the proportions for textures in our last article.
If we get u and v proportions for a given point of intersection P the interpolation is given by:
(1.0 - (u + v)) * P2 Normal + P1 Normal * u + P3 Normal * v
or better:
nx = -( (1.0 - (u + v)) * tData.normalVector(nb).x +
tData.normalVector(na).x * u + tData.normalVector(nc).x * v);
ny = -( (1.0 - (u + v)) * tData.normalVector(nb).y +
tData.normalVector(na).y * u + tData.normalVector(nc).y * v);
nz = -( (1.0 - (u + v)) * tData.normalVector(nb).z +
tData.normalVector(na).z * u + tData.normalVector(nc).z * v);
The function
public override void getNormal(double x, double y, double z,
ref double nx, ref double ny,
ref double nz)
{
tPoint U = new tPoint(tData.point(va).x - tData.point(vb).x,
tData.point(va).y - tData.point(vb).y,
tData.point(va).z - tData.point(vb).z);
tPoint V = new tPoint(tData.point(vc).x - tData.point(vb).x,
tData.point(vc).y - tData.point(vb).y,
tData.point(vc).z - tData.point(vb).z);
tPoint N = new tPoint(x - tData.point(vb).x,y -
tData.point(vb).y,z - tData.point(vb).z);
double dU = tAlgebra.modv(U.x, U.y, U.z);
double dV = tAlgebra.modv(V.x, V.y, V.z);
double dN = tAlgebra.modv(N.x, N.y, N.z);
tAlgebra.Normalize(ref N.x, ref N.y, ref N.z);
tAlgebra.Normalize(ref U.x, ref U.y, ref U.z);
double cost = tAlgebra.Dot3(N.x, N.y, N.z, U.x, U.y, U.z);
if (cost < 0) cost = 0;
if (cost > 1) cost = 1;
double t = Math.Acos(cost);
double distY = 0, distX = 0;
distX = dN * Math.Cos(t);
distY = dN * Math.Sin(t);
double u = distX/ dU;
double v = distY/ dV;
tAlgebra.Normalize(ref tData.normalVector(na).x,
ref tData.normalVector(na).y,
ref tData.normalVector(na).z);
tAlgebra.Normalize(ref tData.normalVector(nb).x,
ref tData.normalVector(nb).y,
ref tData.normalVector(nb).z);
tAlgebra.Normalize(ref tData.normalVector(nc).x,
ref tData.normalVector(nc).y,
ref tData.normalVector(nc).z);
nx = -( (1.0 - (u + v)) * tData.normalVector(nb).x +
tData.normalVector(na).x * u +
tData.normalVector(nc).x * v);
ny = -( (1.0 - (u + v)) * tData.normalVector(nb).y +
tData.normalVector(na).y * u +
tData.normalVector(nc).y * v);
nz = -( (1.0 - (u + v)) * tData.normalVector(nb).z +
tData.normalVector(na).z * u +
tData.normalVector(nc).z * v);
}
Using the code
The samples includding classes and obj file are inside the zip file for download on the top of the article.




 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 






