Introduction
In general, recursion means self repeating patterns. In Mathematics, it can be a function that is defined in terms of itself, such as factorial, Fibonacci etc. In computer programming, recursion means a function that is defined in terms of itself. In other words, a function that calls itself. Every recursive function has a termination condition; otherwise, it will call itself forever, and this condition can be called the base condition.
Usually, recursion is a little bit difficult to understand for most students. Researchers usually come up with different strategies to teach recursion easily for students, such as teach recursion before teaching arrays [4], delegations [2], or recursively generated geometric designs [3].
Types of Recursion
In C++, the types of recursion can be defined in more than one dimension. In one dimension, it can be categorized as runtime recursion and compile time recursion using template meta-programming.
Runtime recursion is the most common recursion technique used in C++. This can be implemented when a C++ function (or member function) calls itself.
In C++, we can also do compile time recursion with the help of template meta-programming. When you instantiate a template class (or structure) in C++, the compiler will create the code of that class at compile time. Just like runtime recursion, we can instantiate the template class itself to perform the recursion. Just like runtime recursion, we also need the termination condition; otherwise, instantiation will go forever, at least theoretically, but, of course, limited to the resources of the computer and the compiler. In template meta-programming, we can specify the termination condition (or base condition) with the help of template specialization or partial template specialization, depending on the termination condition.
One can think that we might do the same thing with the preprocessor of C++, using macros, because they will also be replaced during compilation. In fact, technically, preprocessor replaces all macros even before compilation, so it is not performing at compile time. The preprocessor also has lots of limitations like, there is no debug symbol defined for the debugger because of simple text replacement, but the most critical limitation is it can not be recursive. The section 16.3.4.2 of the Standard of C++ [1] strictly restricts writing macros that call themselves recursively, therefore we can’t do recursive programming using macros just like we do in templates.
The other way to look at recursion is how a recursive algorithm is implemented. Recursive algorithms can be implemented in more than one way, such as linear, tail, mutual, binary, or nested recursion. We can implement them either at compile time using template meta-programming, or at runtime using functions or member functions.
We can represent the different types of recursion using the following diagram. This diagram shows the different types of recursion based on their implementation (i.e., linear, tail, mutual etc.) and when it will be performed.
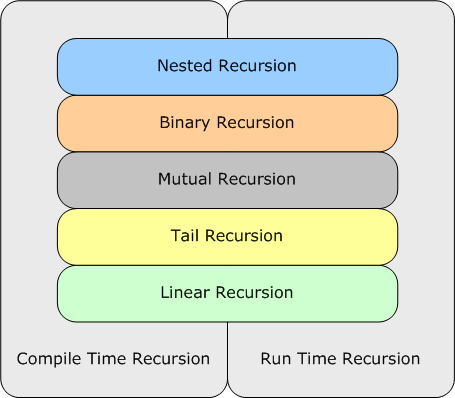
Now, we are going to explore the different types of algorithms one by one, and take a look at their runtime as well as compile time implementations.
Linear Recursion
Linear recursion is the simplest form of recursion, and perhaps the most commonly used. In this recursion, a function simply calls itself until it reaches the termination condition (also known as the base condition); this process is known as winding. After calling the termination condition, the execution of the program returns to the caller; this is known as unwinding.
Functions may perform some additional tasks during winding or unwinding, such as in the case of the factorial function, it will multiply the input number with the return value of the function during the unwinding phase. This process can be demonstrated with the following diagram that shows both the winding and unwinding phase of the factorial function using linear recursion.

Mathematically, we can write the factorial function recursively this way, i.e., when the value of “n” is zero, then return one, and when the value of “n” is greater than zero, then call the function recursively with “n-1” and multiply the result with the return value of the recursive function.

int Factorial(int no)
{
if (no < 0)
return -1;
if (0 == no)
return 1;
return no * Factorial(no - 1);
}
Program 1: Runtime example of linear recursion
The above program is a runtime version of linear recursion. Here, we have a termination condition of 0, and this program starts unwinding when it reaches the termination condition. There is one more error condition in this program to prevent infinite function calls if someone passes a negative number to this function. This function will simply return -1 as an error if the value of the parameter is negative.
template <int No>
struct Factorial
{
enum { value = No * Factorial<No - 1>::value };
};
template <>
struct Factorial<0>
{
enum { value = 1 };
};
Program 2: Compile time example of linear recursion
This program is a compile time counter part of Program 1. Here, we use template instantiation to perform the recursion. We also have a termination condition in the form of a template specialization. This is quite a simple example of template specialization, and we do not have a lot of code, but in a few cases, we might have to rewrite all the code in the template specialization class (or structure) too, because we can’t inherit the code from the template class (or structure) to the specialization class (or structure).
Here, we didn’t even introduce the error condition of a negative number, because this program won't even compile if someone tries to call this with a negative number. This is one very big advantage of compile time recursion that we can’t compile the infinite calling condition. However, the error message is perhaps not very obvious in that case.
Here is a usage of compile time recursion.
cout << Factorial<6>::value << endl;
cout << Factorial<0>::value << endl;
cout << Factorial<-2>::value << endl;
Here, the compiler will refuse to compile the last statement and give a long cryptic error message.
Tail Recursion
Tail recursion is a specialized form of linear recursion where the recursive function call is usually the last call of the function. This type of recursion is usually more efficient because a smart compiler will automatically convert this recursion into a loop to avoid nested function calls. Because a recursive function call is usually the last statement of a function, there isn’t any work done during the unwinding phase; instead, they simply return the value of the recursive function call. Here is an example of the same program converted to tail recursion.

We can define the tail recursion mathematically using this equation, i.e., when the value of “n” is zero, then simply return the value of “a”; if the value of “n” is greater than zero, then call the recursive function by passing “n-a” and “n*a”. Here, you can also notice that during the unwinding phase, every recursive function simply returns the value of “a”.

int Factorial(int no, int a)
{
if (no < 0)
return -1;
if (0 == no || 1 == no)
return a;
return Factorial(no - 1, no * a);
}
Program 3: Runtime example of tail recursion
This is a modified version of the linear recursion program. Here, we perform all the calculations before calling the recursive function, and simply return whatever value we got from the recursive function. Here, the calculation order is the reverse of the linear recursion. In linear recursion, we first multiply 1 with 2, then its result with 3, and so on; on the other hand, here we multiply n with n-1, then with n-2, until we reach 0.
template <int No, int a>
struct Factorial
{
enum { value = Factorial<No - 1, No * a>::value };
};
template <int a>
struct Factorial<0, a>
{
enum { value = a };
};
Program 4: Compile time example of tail recursion
Here is the compile time version of the same program doing the same thing at compile time.
Tail recursion is very useful and some times unavoidable in functional languages, because they might not have a looping construct. They usually perform the looping with the help of tail recursion. You can do almost everything with tail recursion that can be done with looping, but this is usually not true in reverse. Here is a very simple example to demonstrate looping via tail recursion:
void RecursiveLoop(int n)
{
if (0 == n)
return;
cout << n << endl;
return RecursiveLoop(--n);
}
Program 5: Demonstration of looping via tail recursion - simple version
But, this program looks very rigid, and we can not customize it. With the help of templates and function objects, we can customize this function so you can control each individual piece of it. Here is a modified version of the same program where we can control each and every part of it.
template <typename TType, typename TTerminate, typename TAction, typename TStep>
void RecursiveLoop(TType n)
{
if (TTerminate()(n))
return;
TAction()(n);
return RecursiveLoop<TType, TTerminate, TAction, TStep>(TStep()(n));
}
Program 6: Demonstration of looping via tail recursion - template version
Here is the default implementation of “Termination condition”, “Action to be performed”, and “Stepping of the loop”.
template <typename T>
class IsTerminate
{
public:
bool operator () (T n)
{
return n == 0 ? true : false;
}
};
template <typename T>
class Step
{
public:
T operator () (T n)
{
return --n;
}
};
template <typename T>
class Action
{
public:
void operator () (T n)
{
cout << n << endl;
}
};
Program 6: Implementation of each step for recursive loop via tail recursion - template version
And, here is a simple usage of this function:
RecursiveLoop<int, IsTerminate<int>, Action<int>, Step<int> >(10);
We can not give the default implementation in the “RecursiveLoop” function because C++ doesn’t allot the default template parameter to the function template. We can do this only in the case of a C++ class. To overcome this situation, we can make a “RecursiveLoop” function object instead of a simple function and passe the default action as the default parameter, so its calling will be much simpler. Here is the revised version of the existing program:
template <typename TType,
typename TTerminate = IsTerminate<TType>,
typename TAction = Action<TType>,
typename TStep = Step<TType>
>
class RecursiveLoop
{
public:
void operator ()(TType n)
{
if (TTerminate()(n))
return;
TAction()(n);
return RecursiveLoop<TType, TTerminate, TAction, TStep>()(TStep()(n));
}
};
Program 7: Implementing looping via tail recursion using a function object and a default template parameter
Now, the usage of this function object is very simple.
RecursiveLoop<int>()(10);
Mutual Recursion
Mutual recursion is also known as indirect recursion. In this type of recursion, two or more functions call each other in a circular way. This is the only way of doing recursion if the programming language doesn’t allow calling functions recursively. The termination condition in this recursion can be in one or all of the functions.

Mathematically, we can define these functions as:


bool isEven(int no)
{
if (0 == no)
return true;
else
return isOdd(no - 1);
}
bool isOdd(int no)
{
if (0 == no)
return false;
else
return isEven(no - 1);
}
Program 8: Runtime example of mutual recursion
This is the most primitive example of mutual recursion. We know that zero is an even number and 1 is an odd number. If we want to check whether a number is even or odd, then we can call these functions, which internally call each other by subtracting one from the input value until the base condition is reached. Of course, this is not the best way to implement this algorithm; it will take a lot of resources to check whether a number is even or odd. In addition, if someone passed a negative number, then they will keep calling each other, and eventually throw a stack overflow error at run time.
template <int no>
struct isEven
{
enum { value = no == 0 ? 1 : isOdd<no - 1>::value };
};
template <>
struct isEven<0>
{
enum { value = 1 };
};
template <int no>
struct isOdd
{
enum { value = no == 0 ? 0 : isEven<no - 1>::value };
};
template <>
struct isOdd<0>
{
enum { value = 0 };
};
Program 9: Compile time example of mutual recursion
Here is the compile time version of the same program. The only difference between this program and the above one is that it will not even compile if we try to pass a negative number to it.
Determining whether a number is even or odd using mutual recursion is not a very good idea. A more interesting example is male sequence and female sequence. Both functions recursively call each other, and can be defined as:


Here is the runtime and compile time versions of the Male and Female functions, using mutual recursion:
int MaleSequence(int n)
{
if (0 == n)
return 0;
return n - FemaleSequence(MaleSequence(n-1));
}
int FemaleSequence(int n)
{
if (0 == n)
return 1;
return n - MaleSequence(FemaleSequence(n-1));
}
Program 10: Runtime mutual recursion implementation of the Male and Female functions
template <int n>
struct MaleSequence
{
enum { value = n - FemaleSequence<MaleSequence<n - 1>::value>::value };
};
template <>
struct MaleSequence<0>
{
enum { value = 0 };
};
template <int n>
struct FemaleSequence
{
enum { value = n - MaleSequence<FemaleSequence<n - 1>::value>::value };
};
template <>
struct FemaleSequence<0>
{
enum { value = 1 };
};
Like other compile time recursion functions, we have to do template specialization for both functions to handle the termination condition.
Binary Recursion
In binary recursion, the recursive function calls itself twice, not once. This type of recursion is very useful in some data structures like traversing a tree in prefix, postfix, or infix order, generating Fibonacci numbers etc.
Binary recursion is a specific form of exponential recursion where one function calls the recursive function more than once (in case of binary, two). In other words, recursive functions call exponentially in this type of recursion.

Mathematically, we can define the Fibonacci sequence as:

int Fib(int no)
{
if (no < 1)
return -1;
if (1 == no || 2 == no)
return 1;
return Fib(no - 1) + Fib(no - 2);
}
Program 12: Runtime example of binary recursion
Here is a simple implementation of Fibonacci numbers calling the recursive function twice. Here we have two base cases, when the value of input parameter is 1 and 2. This is, of course, not the best implementation of Fibonacci numbers, and we can convert it into tail recursion by changing it a little bit. But, before converting this one into tail recursion, take a look at the compile time version of binary recursion.
template <int n>
struct Fib
{
enum { value = Fib<n - 1>::value + Fib<n - 2>::value };
};
template<>
struct Fib<2>
{
enum { value = 1 };
};
template <>
struct Fib<1>
{
enum { value = 1 };
};
Program 13: Compile time example of binary recursion
In the compile time version of binary recursion, we specialize the template class (or structure) twice. In general, we have to do template specialization in every base case.
int Fib(int n, int a, int b)
{
if (1 == n)
return b;
else
return Fib(n-1, b, a+b);
}
Program 14: Runtime example of converting binary recursion into tail recursion
Here, we convert binary recursion into tail recursion. We simply perform the calculation before calling any recursive function, therefore we do not need to call the recursive function twice. In Fibonacci numbers, we always need the last two numbers, so after performing the calculation on the last two numbers, we just discard the first one, i.e., “a”, and replace the second one in place of the first, i.e., place the value of “b” in “a”, and calculate the next number.
Mathematically, we can define this as:

template <int n, int a, int b>
struct Fib
{
enum { value = Fib<n-1, b, (a+b)>::value };
};
template<int a, int b>
struct Fib<1, a, b>
{
enum { value = b };
};
Program 15: Compile time example of converting binary recursion into tail recursion
Here is the compile time version of this program. Here, we have only one termination condition (i.e., base case), therefore we need only one template specialization. Here, we perform partial template specialization because we want the last calculated value in the base case when the value of n is equal to 1.
Nested Recursion
This is a special type of recursion when the recursive call is nested. All of the above recursions can be replaced with either simple looping or looping with stack, but this type of recursion can not be easily replaced by a simple loop.
One typical example of nested recursion is the Ackermann function. Here is a simple diagram of the Ackermann function to demonstrate nested recursion. We explicitly select a small value as a parameter, for simplicity.

Mathematically, the Ackermann function is defined as:

int Ackermann(int m, int n)
{
if (m < 0 || n < 0)
return -1;
if (0 == m)
return n + 1;
else if (m > 0 && 0 == n)
return Ackermann(m-1, 1);
else
return Ackermann(m-1, Ackermann(m, n-1));
}
Program 16: Runtime example of nested recursion
Here is the runtime implementation of nested recursion. This function has two termination conditions; one condition terminates the nested calls and starts performing linear recursion, and the other termination condition stops the linear recursion. The first “if” condition is for error checking.
template <int m, int n>
struct Ackermann
{
enum { value = Ackermann<m-1, Ackermann<m, n-1>::value>::value };
};
template <int m>
struct Ackermann<m, 0>
{
enum { value = Ackermann<m-1, 1>::value };
};
template <int n>
struct Ackermann<0, n>
{
enum { value = n + 1 };
};
Program 17: Compile time example of nested recursion
In compile time version of nested call we have to do template specialization twice because of two termination condition. The first specialization stops the nested call and start doing linear recursion and the second specialization stops the linear recursion.
Template Recursion
All the programs we discussed above either run completely at compile time or at runtime. We can make a program that can use both compile time as well as time features. One such example is instantiating an object at compile time using compile time recursion and then using it at runtime. For example, if we want to create a class of multi-dimensional arrays, then we can pass the dimension, with type, as a parameter and create an object of the same class with one less dimension inside. When the dimension reaches one, we can stop it with template specialization and provide implementation of a one dimensional array. We can represent this concept with the following diagram.

Here is a simple implementation of this. Just to make it simple, I avoid const correctness, use std::vector, and give the minimum possible interface of this class.
template <typename T, int Dim>
class Array
{
private:
Array<T, Dim - 1> vecRow;
public:
Array(int iSize = 0)
{
vecRow.Resize(iSize);
}
void Resize(size_t iSize)
{
vecRow.Resize(iSize);
}
size_t Size()
{
return vecRow.Size();
}
Array<T, Dim - 1>& operator [] (size_t x)
{
if (x >= 0 && x < vecRow.Size())
{
return vecRow;
}
throw std::out_of_range("Index is out of range");
}
};
template <typename T>
class Array<T, 1>
{
private:
std::vector<T> vecRow;
public:
Array(int iSize = 10)
{
Resize(iSize);
}
void Resize(size_t iSize)
{
vecRow.resize(iSize);
}
size_t Size()
{
return vecRow.size();
}
T& operator [] (size_t x)
{
if (x >= 0 && x < vecRow.size())
{
return vecRow.at(x);
}
throw std::out_of_range("Index is out of range");
}
};
Program 18: Multidimensional class using template recursion
And, here is the usage of this class:
Array<int, 3> obj(10);
obj[0][0][0] = 100;
obj[0][1][0] = 200;
obj[1][2][0] = 300;
obj[0][3][0] = 400;
In this example, object creation is performed at compile time using the template recursion technique. Once the object is created, then its method will be called at runtime.
Acknowledgments
I’d like to thank “Tafseer Ahmed” and “Shahzaib Saleem” for reading this and giving me their useful comments and pointing out several mistakes in the initial draft, to make it better.
References
- Programming Language ISO/IEC 14882, 2003
- Teaching and viewing recursion as delegation, Jeffrey Edgington
- Teaching recursion using recursively generated geometric design, Aaron Gordon
- Why Structure Recursion should be taught before Arrays in CS1, Kim B. Bruce, Andrea Danyluk, Thomas Murtagh
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 








