Introduction
Magic square is an ancient mathematical problem that many people try to solve. May be you see it in some magazines or your teacher might have introduced it in a class.
Details
A magic square is an arrangement of numbers from 1 to n2 in an [n x n] matrix, with each number occurring exactly once, and such that the sum of the entries of any row, any column, or any main diagonal is the same.
It is not hard to show that this sum must be n [ ( n2 + 1) / 2 ]. If we use this formula for that example output which is below, for [5x5] matrix; 5 [ ( 52 + 1 ) / 2 ] = 65.
| 17 | 24 | 1 | 8 | 15 | 65 |
| 23 | 5 | 7 | 14 | 16 | 65 |
| 4 | 6 | 13 | 20 | 22 | 65 |
| 10 | 12 | 19 | 21 | 3 | 65 |
| 11 | 18 | 25 | 2 | 9 | 65 |
| 65 | 65 | 65 | 65 | 65 | 65 |
Now, I want to show you a way to calculating magic squares in any order by using your talented computer.
Siamese method
This method is useful for calculating magic squares with odd order. It begins by placing a 1 in any location (in the center square of the top row in the above example), then incrementally placing subsequent numbers in the square one unit above and to the right. The counting is wrapped around, so that falling off the top returns on the bottom and falling off the right returns on the left. When a square is encountered which is already filled, the next number is instead placed below the previous one and the method continues as before. The method, also called de la Loubere's method.
For example, if order of square is 5, we have:
void CalculateOddMagicSquare()
{
n=5;
int matrix[5][5];
int nsqr = n * n;
int i=0, j=n/2;
for (int k=1; k<=nsqr; ++k)
{
matrix[i][j] = k;
i--;
j++;
if (k%n == 0)
{
i += 2;
--j;
}
else
{
if (j==n)
j -= n;
else if (i<0)
i += n;
}
}
}
Here is a very nice flash animation to show you how to fill square's cells. Thanks KIVANÇ HiKMET ANAR, for his flash.
Complete Work
Below is full source code of calculating magic squares in any order.
#include "stdafx.h"
#include <vector>
using namespace std;
void OddMagicSquare(vector<vector<int> > &matrix, int n);
void DoublyEvenMagicSquare(vector<vector<int> > &matrix, int n);
void SinglyEvenMagicSquare(vector<vector<int> > &matrix, int n);
void MagicSquare(vector<vector<int> > &matrix, int n);
void PrintMagicSquare(vector<vector<int> > &matrix, int n);
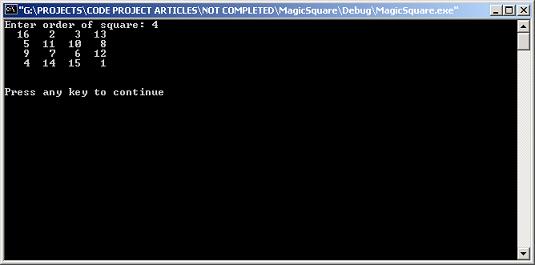
int main(int argc, char* argv[])
{
int n;
printf("Enter order of square: ");
scanf("%d", &n);
vector<vector<int> > matrix(n, vector<int> (n, 0));
if (n<3)
{
printf("\nError: n must be greater than 2\n\n");
return -1;
}
MagicSquare(matrix, n);
PrintMagicSquare(matrix, n);
return 0;
}
void MagicSquare(vector<vector<int> > &matrix,int n)
{
if (n%2==1)
OddMagicSquare(matrix, n);
else
if (n%4==0)
DoublyEvenMagicSquare(matrix, n);
else
SinglyEvenMagicSquare(matrix, n);
}
void OddMagicSquare(vector<vector<int> > &matrix, int n)
{
int nsqr = n * n;
int i=0, j=n/2;
for (int k=1; k<=nsqr; ++k)
{
matrix[i][j] = k;
i--;
j++;
if (k%n == 0)
{
i += 2;
--j;
}
else
{
if (j==n)
j -= n;
else if (i<0)
i += n;
}
}
}
void DoublyEvenMagicSquare(vector<vector<int> > &matrix, int n)
{
vector<vector<int> > I(n, vector<int> (n, 0));
vector<vector<int> > J(n, vector<int> (n, 0));
int i, j;
int index=1;
for (i=0; i<n; i++)
for (j=0; j<n; j++)
{
I[i][j]=((i+1)%4)/2;
J[j][i]=((i+1)%4)/2;
matrix[i][j]=index;
index++;
}
for (i=0; i<n; i++)
for (j=0; j<n; j++)
{
if (I[i][j]==J[i][j])
matrix[i][j]=n*n+1-matrix[i][j];
}
}
void SinglyEvenMagicSquare(vector<vector<int> > &matrix, int n)
{
int p=n/2;
vector<vector<int> > M(p, vector<int> (p, 0));
MagicSquare(M, p);
int i, j, k;
for (i=0; i<p; i++)
for (j=0; j<p; j++)
{
matrix[i][j]=M[i][j];
matrix[i+p][j]=M[i][j]+3*p*p;
matrix[i][j+p]=M[i][j]+2*p*p;
matrix[i+p][j+p]=M[i][j]+p*p;
}
if (n==2)
return;
vector<int> I(p, 0);
vector<int> J;
for (i=0; i<p; i++)
I[i]=i+1;
k=(n-2)/4;
for (i=1; i<=k; i++)
J.push_back(i);
for (i=n-k+2; i<=n; i++)
J.push_back(i);
int temp;
for (i=1; i<=p; i++)
for (j=1; j<=J.size(); j++)
{
temp=matrix[i-1][J[j-1]-1];
matrix[i-1][J[j-1]-1]=matrix[i+p-1][J[j-1]-1];
matrix[i+p-1][J[j-1]-1]=temp;
}
i=k;
j=0;
temp=matrix[i][j]; matrix[i][j]=matrix[i+p][j]; matrix[i+p][j]=temp;
j=i;
temp=matrix[i+p][j]; matrix[i+p][j]=matrix[i][j]; matrix[i][j]=temp;
}
void PrintMagicSquare(vector<vector<int> > &matrix, int n)
{
for (int i=0; i<n; i++)
{
for (int j=0; j<n; j++)
printf(" %3d", matrix[i][j]);
printf("\n");
}
printf("\n\n");
}
Conclusion
Enjoy!
I was born in Shiraz, a very beautiful famous city in Iran. I started programming when I was 12 years old with GWBASIC. Since now, I worked with various programming languages from Basic, Foxpro, C/C++, Visual Basic, Pascal to MATLAB and now Visual C++.
I graduated from
Iran University of Science & Technology in Communication Eng., and now work as a system programmer for a telecommunication industry.
I wrote several programs and drivers for Synthesizers, Power Amplifiers, GPIB, GPS devices, Radio cards, Data Acquisition cards and so many related devices.
I'm author of several books like Learning C (primary and advanced), Learning Visual Basic, API application for VB, Teach Yourself Object Oriented Programming (OOP) and etc.
I'm winner of January, May, August 2003 and April 2005 best article of month competition, my articles are:
You can see list of my articles, by clicking here
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 










