Introduction
Simpson’s rule is a simple and effective technique for numerically evaluating integrals. However, practical implementation requires more than is often presented in introductions to the method. This article will show how to implement the algorithm n C# and will discuss how to prepare integrals for evaluation.
Background
Calculus books often give a quick introduction to the trapezoid rule and Simpson’s rule as ways to approximately calculate integrals that cannot be computed exactly by hand.
Given an interval [a, b] and an even number n, Simpson’s rule approximates the integral
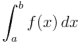
by
![\frac{h}{3} \left[f(x_0) + 4 f(x_1) + 2 f(x_2) + 4 f(x_3) + 2f(x_4) + \cdots + 4 f(x_{n-1}) + f(x_n) \right]](data:image/gif;base64,R0lGODlhAQABAAAAACH5BAEKAAEALAAAAAABAAEAAAICTAEAOw==)
where h = (b - a)/n and xi = a + ih.
While that is a correct description of the algorithm, it leaves two related questions unanswered:
- How good is the approximation?
- How should I choose n?
In practice you seldom know before you start how large n needs to be in order to meet your accuracy requirements. If you can estimate your error at runtime, you can use that estimate to determine n.
A common approach is to repeatedly apply Simpson’s rule, doubling the number of integration points at each stage. The difference between two successive stages gives an estimate of the error, so you continue doubling the stages until the error estimate is below your tolerance.
There are a couple practical matters to implementing this approach. First, if naively implemented, the method will re-evaluate the integrand at the same points multiple times. At each new stage, half of the integration points are the same as they were at the previous stage. A little algebra makes it possible to reuse the integral estimate from the previous stage and only evaluate the integrand at the new integration points.
The second practical implementation matter is to not check the stopping condition too soon. If you check the stopping rule after each stage, it is possible in the early stages that your integration points miss regions of variability in your integrand and you are led to believe the method has converged when it has not. The code given here only checks for convergence after five stages of Simpson’s rule.
Using the Code
The class SimpsonIntegrator has only two methods, overloaded implementations of Integrate. The simpler version of Integrate returns nothing but the value of the integral. The more detailed version returns the number of function evaluations used and an estimate of the error. The simpler version is implemented by calling the more detailed method and discarding the extra information. Also, the more detailed version allows the user to specify the maximum number of integration stages; the simpler version sets a default value for this parameter.
Here is an example integrating the function f(x) = cos(x) + 1 over the interval [0, 2π]:
double twopi = 2.0*Math.PI;
double epsilon = 1e-8;
double integral = SimpsonIntegrator.Integrate(x => Math.Cos(x) + 1.0, 0,
twopi, epsilon);
double expected = twopi;
Assert.IsTrue(Math.Abs(integral - expected) < epsilon);
Note that C#'s support for implicit functions is handy for simple integrands.
According to the theoretical derivation of Simpson’s rule, the method should integrate polynomials up to degree three exactly with only one stage of integration. Here's an example of calling the more detailed interface to specify that the method should use only one stage to integrate f(x) = x3 over an interval [a, b]. We also verify that the code respected our request to only use one stage by checking that the integrand is only evaluated three times. (The first stage of Simpson’s rule evaluates the integrate at each end of the interval and at the midpoint.)
double a = 2, b = 5;
double epsilon = 1e-10;
double integral;
int functionEvalsUsed;
double estimatedError;
double expected;
int maxStages = 1;
integral = SimpsonIntegrator.Integrate(x => x*x*x, a, b, epsilon,
maxStages, out functionEvalsUsed, out estimatedError);
expected = (b*b*b*b - a*a*a*a)/4.0;
Assert.AreEqual(functionEvalsUsed, 3);
Assert.IsTrue(Math.Abs(integral - expected) < epsilon);
Simpson’s rule only applies to smooth functions on a closed interval. If this does not describe your integral, it may still be possible to apply the method after a little preparation. On the other hand, naively applying the method directly where it is not appropriate can give poor results.
A function with a kink in the middle is not smooth and so Simpson’s rule does not directly apply. However, such a function can simply divided into two integrals where the integrand is smooth over both separately. For example, to integrate the function exp(-|x|) over [-3, 5], we would need to split the problem into one integral over [-3, 0] and another over [0, 5] because the integrand has a sharp bend at 0.
An integral over an infinite range cannot be computed by Simpson’s rule directly. However, it is often possible to use a change of variables to convert the integral into a well-behaved integral over a finite range.
Simpson’s rule also does not apply to functions that become infinite. See Care and treatment of singularities for an example of how to use Simpson’s rule for such integrals.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 






 the trick of reusing previously evaluated points.
the trick of reusing previously evaluated points.
