Applying algorithm of the Chaos Theory on development of the new technology of compression of audio data.
4.97/5 (47 votes)
This article presents brief review on fractal transformation - element of the Chaos Theory and presents its real implementation - new technology of compression of audio data.
Introduction
I have an interest for such weird branch of math as the Chaos Theory. I spent much time on studying of it and resolving of problems with implementation of its into the real tasks. I had postgraduate education and got science degree with the thesis about implementation of element of the Chaos Theory – Fractal Transformation in the task of processing of images. The results of that science work were published in my book: Algorithms of Fractal Compression of Image . Now I have decided to present some result of my research in the field of applying of fractal transformation in the task of compression of audio data.
This article presents brief review on fractal transformation – element of the Chaos Theory and presents its real implementation – the new technology of compression of audio data.
What you WILL NOT FIND there:
- Complex equations. More complex definition of fractal transformation you can find in many books. For instance, in my book: Algorithms of Fractal Compression of Image.
- Abstract ideas (may be just a couple).
- Any generators of fractal images. You can find thousands such programs for generating image of fractals on the Internet, but no one of them is not resolve any real task (except the task to get nice view picture).
What you WILL FIND there:
- Brief view on how fractal transformation can be applyed to the real task. More information can be found in my book: Algorithms of Fractal Compression of Image (it is not a promotion action :)).
- Unusual physical interpretation of fractal transformation. It can help to pay your attantion on it.
- REAL CODE OF ENCODER AND DECODER OF COMPRESSION OF AUDIO DATA BY FRACTAL TRANSFORMATION. The presented soft allows to encode the raw WAVE format file into the file of new format and decode it back into WAVE format file (or just simple plays it in the embedded player).
- Description of a new format for storing encoded audio data with FIVE UNIQUE FEATURES, which cannot be found in any well known industrial audio formats.
Background
I have been interested by the Chaos Theory many years ago and paid much time on studying of it and way of applying of it in the real task. I have got some result of those researches and have decided to present some of them there. I think that some readers of this article will pay attention on fractal transformation and will try to apply it in their projects (and may be buy my book :)).
Let's go.
Brief history review
If you type 'fractal' in the search bar of "CodeProject" then you find many links on articles about fractals, but almost all of them use fractal transformation for creating images in the different forms. For example: The beauty of fractals - A simple fractal rendering program done in C#, Visualizing Fractals. You can ask - what about its implementation in the real tasks? You can find a couple books about 'How to earn much money on stock by fractals', but I think that it would be more interesting to see examples from the branch of signal processing.
I spent much time on research of progress in applying of fractals to the task in IT industry and I can say that there were only some attempts to do it. Two of them are very interesting in my view:
- Video codec - 'ClearVideo' by company Iterated System.
- Image/video codec - 'FIASCO' by Ullrich Hafner
You can ask - Why I have not heart about it? So, the mentioned codecs were developed in 90s of 20th Century and now they are collapsated: according to site 'MultimediaWiki' - 'Iterated Systems developed the ClearVideo codec. They are apparently no longer in business.', and the developer of 'FIASCO' posted last news on 11/28/2000 - '11/28/2000: FIASCO 1.3 is released. This release fixes a rendering bug for 24bpp displays. Moreover, the first release of a FIASCO GIMP plugin is available (input support only).'. However, before to understand why they were not successed it would be useful to present how they work.
Mathematicial basement
The idea of the fractal image encoding-decoding - to build fractal image which is close to the original image. Of course, if you look at visualisation of the Mandelbrot fractal set which is generated by the next equation then you you say it is not a real image.
Z(n+1) = Zn2 + C where n = 1, 2, 3, ...

However, the fact is that very complex visualisation can be reached by very simple equation. It leads to the next question - Is it possible to find such equation which can generate set which is identical to the original set (for example set of points - real image)? In many books you can find that it is possible (especially in the ONE BOOK which must be on the top of other books, in my view :)).
More correctly, I can say that it is possible to find such fractal transformation, which can generate image with distortions less or equal than any predefined value. It means that generated image can be differ from the original one in value which cannot be marked by viewer due to redundancy of visual information in image. So, fractal image encoding-decoding is LOSSY quality image processing technique.
PIFS schema
You can ask - How to do a fractal encoding (or more correct - a fractal analyse)? Of course, the visualisation of the Mandelbrot fractal set is impressing, but it was developed after many years of the research. It is a nonsense to set people before tables, give pictures and order to find the suitable equations (however, the first solutions were very similar to it). Solution of that problem was proposed by Michael Barnsley and his aspirants (first of them started Iterated Systems Incorporated). They proposed partitioned iterated function systems (PIFS). That technique copies the original image into two sets: ragns and domains, then computer matches each rang to a domain and produces an affine transformation from the domain to the rang.


The transformations are stored into the output file, and if the size of the result file is less then the size of the original image file - we have compression. The main idea is to find the system of local functions  . The fact is that analitical fractal transformation of Mandelbrot or geomentrical fractal transformation of Sierpinski (Sierpinski triangle) have the global similarity - each part of those sets are simular to all those sets. However, it is almost imposible to find the global similarity in the real images. We can only find that, for exmaple, one small part of image very similar to other small part which is very similar to the third one which is similar to the first one.
. The fact is that analitical fractal transformation of Mandelbrot or geomentrical fractal transformation of Sierpinski (Sierpinski triangle) have the global similarity - each part of those sets are simular to all those sets. However, it is almost imposible to find the global similarity in the real images. We can only find that, for exmaple, one small part of image very similar to other small part which is very similar to the third one which is similar to the first one.
You can see that PIFS covers whole image and sets the relations between different parts of image. It creates system of simple equations which can be usen for describing of image. That approach for processing of image is very different from the classical idea of linear interpolation of signals. As a result, for understanding of it we need to know three facts about fractal transformations for understanding of working of PIFS:
- fractal transformation is recursion — it is based on the idea of self-similarity;
- fractal transformation is shrink – it means that copy always smaller than original;
- space of fractal transformation is compact – all operations on the set is reflected on itself.
A more precise definition is enought complex and is not great interest from the view point of applying. Lets consider the use of fractal transformation on the basis of the following expression:

there  - transformation in space of set;
- transformation in space of set;  - shrinking transformation of vector with length of
- shrinking transformation of vector with length of  into the vector with length of
into the vector with length of 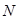 , but what do
, but what do  and
and  mean? Variables
mean? Variables  and
and  describe transformation in space, but each pixel has a special value – luminance, and it must be considered as part of fractal transformation space:
describe transformation in space, but each pixel has a special value – luminance, and it must be considered as part of fractal transformation space:  - shrink transformation of luminance,
- shrink transformation of luminance,  - offset of luminance.
- offset of luminance.
So, what are we should doing with it, ask you? It is simple – such operation is executed for all rangs  which cover the original image. And again, and again. After infinitive repetitions we get very complex image which includes drawing molecules, atoms and quarks :). In the reality, it is much more simple – after each recursion iteration of decoding the result image becomes more close to the original one in big objects, and distorsions are remarkable in smaller ones (more correct definition you can find in the BOOK). There is a question – what will happened if the size of small objects with distorsions has become less then resolution of digital image (real space of digital image is DISCRET – Kotelnikov's theorema). So, the answer is simple – those objects will drop down between samples of image. It will happens after about
which cover the original image. And again, and again. After infinitive repetitions we get very complex image which includes drawing molecules, atoms and quarks :). In the reality, it is much more simple – after each recursion iteration of decoding the result image becomes more close to the original one in big objects, and distorsions are remarkable in smaller ones (more correct definition you can find in the BOOK). There is a question – what will happened if the size of small objects with distorsions has become less then resolution of digital image (real space of digital image is DISCRET – Kotelnikov's theorema). So, the answer is simple – those objects will drop down between samples of image. It will happens after about 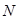 recursion iterations, and any execution of equation will not reflect on the result image. This is way of decoding fractal image.
recursion iterations, and any execution of equation will not reflect on the result image. This is way of decoding fractal image.
I expecte the next question – how to find the mentioned coefficients of fractal transformation? It is nonsense to set a person before table, give original image, ruler and give task to find for each rang  the suitable domain
the suitable domain  and coefficients
and coefficients  ,
,  ,
,  . So, the task of searching the suitable fractal transformation – fractal analysis, can be automated be the next equation:
. So, the task of searching the suitable fractal transformation – fractal analysis, can be automated be the next equation:

The task includes finding pair  , which has the minimum length of vector
, which has the minimum length of vector  . If we set that value to zero – the best case, then it is possible to find the partial solution for coefficients
. If we set that value to zero – the best case, then it is possible to find the partial solution for coefficients  and
and  :
:


Equations are not complex, but the main reason the actual failure of the implementation of the fractal transformation in the area of image compression - the need of finding for every rang the suitable domain with minimum value of  . It can be compared with the task of “Salesman” - rangs are the cities and roads are combinations rangs with domains with length
. It can be compared with the task of “Salesman” - rangs are the cities and roads are combinations rangs with domains with length  . The problem is that the length of each road is unknown. We have to go along each of them and measure them before selecting the shortest one. It can take hours for image.
. The problem is that the length of each road is unknown. We have to go along each of them and measure them before selecting the shortest one. It can take hours for image.
You can ask – it is OK, but how about the topic of article – compression of audio? The answer is simple – fractal transformation binds abstract meaning of Set: set of points in digital image, set of samples in digital audio stream or set of galaxies in the Universe. All presented above equations are the same for digital space of image and sound. It does not mean what about are we thinking, when use vectors  and
and  - set pixels of images or set samples of audio stream – the math is same.
- set pixels of images or set samples of audio stream – the math is same.
How is it realized?
Using the code
So, the source code can be found there - https://github.com/Xirexel/ROAD, and also compiled files for Windows platform: Audio_Fractal_Bin.zip. The project is written on Qt framework(C++) and can be easy replaced on any supported platform. The project is divided on five parts:
TEMPLATE = subdirs
SUBDIRS += \
Audio_Fractal_Encoder_Library\
Audio_Fractal_Encoder_Widget\
Audio_Fractal_Decoder_Library\
Audio_Fractal_Decoder_Widget\
Audio_Fractal_GUI
Audio_Fractal_GUI – general widget for linking the widgets of encoder and decoder;
Audio_Fractal_Encoder_Widget – widget for supporting GUI of encoder;
Audio_Fractal_Decoder_Widget – widget for supporting GUI of decoder;
Audio_Fractal_Encoder_ Library – library for execution of encoding;
Audio_Fractal_Decoder_ Library – library for execution of decoding.
Firts, second and third modules are used for presenting GUI and do not have the great interest. Encoder and decoder are much more interesting. The architect of those modules are developed by UML modeling.
Module library of encoder includes 26 classes and interfaces. UML schema is big and cannot be presented there (you can find it on link - Download FractalEncoding.pdf). However, it is possible to mention some of them:
Audio_Fractal_Encoder— main class which execute of the management of encoding;DataBuffer— class for storing samples of audio stream;Domain— class for storing samples of one domain;DomainPool— class for management of set of domains;FractalItem— class for storing coefficients of fractal transformation;FrameFractalItemCollection— class for management of set of instances of FractalItem class;FractalDataContainer— class for management and storing of packed coefficients of fractal transformations before saving in out file;FractalEncoder— class which executes fractal analysis;FractalEncodingOptions— class for storing configuration of fractal analysis.
Widget of encoder has the next view:

In the process of encoding each encoded frame is partitioned by BinTree schema.
The general algorithm is simple:
- code gets 10 frames from the original audio stream – superframe;
- mixing data in channel for reducing inter-channel redundancy;
- take one frame with length of 2048 samples;
- copy frame in the pool of domains;
- consider whole frame as a silence block;
- compute the value of distortion of sound samples in silence block. If the value is less than silence threshold – block is marked as a silence block and IS NOT ENCODED – step on the previous stage.
- If the value is more then the silence threshold — the block is partitioned by BinTree schema;
- If the length of a new block is more than maximum length of rang (32 samples) – go to 5th step;
- If the length of a new block is less than maximum length of rang (32 samples), but more then maximum length of rang (4 samples), then code executes search for that block the best domain with the minimum error or splits block by BinTree schema go to 9th step;
- If the length of the new block is less than minimum length of rang (4 samples), then the previous block is the smallest and its coefficients of fractal transformation is stored in file. Go to the next block;
The next values are stored in file:
bit of silence,
number of domain J,
index of transformation  ;
;
value of  ,
,
value of  .
.
It is enough for decoding, which is executed by Audio_Fractal_Decoder_ Library. UML schema classes of decoder is presented on next link - Download FractalDecoding.pdf. The schema is simple (however, it includes 26 classes and interfaces). GUI has the next view:

The code of project is enough huge, but it is possible to present the short section of encoding cycle:
FractalEncoding::Audio_Fractal_Encoder encoder(lptrReader.get(), lptrWriter.get(), options);
bool isRunning = true;
while(isRunning)
{
result = encoder.doEncoding();
switch(result)
{
case FractalEncoding::ERROR:
{
isRunning = false;
}
break;
case FractalEncoding::DONE:
break;
case FractalEncoding::FINISHFILE:
{
isRunning = false;
}
break;
}
qint32 percent = lptrReader->getPercentOfProcessedFile();
if(percent < 0)
break;
emit progressValue(percent);
if (QThread::currentThread()->isInterruptionRequested())
{
result = FractalEncoding::ERROR;
break;
}
}
if(result == FractalEncoding::ERROR)
{
lptrWriter->reject();
}
else
{
lptrWriter->flushAndCloseFile();
}
Instance of FractalEncoding::Audio_Fractal_Encoder class - encoder is created with the three arguments:
lptrReader.get() - pointer on audio data reader,
lptrWriter.get() - pointer on fractal pack writer,
options - instance of options container class.
Execution of fractal analyse is doing by calling method encoder.doEncoding(). We get variable result which presents the result of processing.
The next code is used for presenting of persentage of precessing progress:
qint32 percent = lptrReader->getPercentOfProcessedFile();
if(percent < 0)
break;
emit progressValue(percent);
After go out of processing loop the code flush fractal data to out put file or reject its:
if(result == FractalEncoding::ERROR)
{
lptrWriter->reject();
}
else
{
lptrWriter->flushAndCloseFile();
}
So, it is a simple description of 'How it works'.
Points of Interest
Features:
- Prelistening.
If you have some experience with format compression of image JPEG2000 then you know the similar word - preview. However, what does it mean for audio file? If you look at equation for computing of
 , than you can see that it includes computing average values for domains and rangs – the average value of samples. As a result, we get the next equation:
, than you can see that it includes computing average values for domains and rangs – the average value of samples. As a result, we get the next equation:
This equation is enough complex, but it shows the one important fact – part of packed data can be considered as an average, low sampled version of the original audio stream with low sample rate. It is right, because any fractal transformation needs the initial point - “seed” for growing up the result set. This “seed” can be small version of the result set (due to similarity of fractal transformation). It leads to the next feature of format.
- Some fractal transformation coefficients can be interpretated as low sample rate version of the original audio track. It leads to the next idea - consider the fractal compression as a top level of stack of encoders which produce coefficients and low sampled stream. The low sampled stream can be encoded by other, well known industrial encoder. The result file can look like WELL KNOWN INDUSTRIAL FORMAT and can be played on any player, which support that industrial format. However, the player WILL PLAY IT WIHOUT ANY PROBLEM WITH LOW SAMPLED QUALITY. The another part will be hiden from the regular player. Only the special player can play the file in the full quality. For presenting this feature I selected wll known format WAVE from Microsoft.

The fact is that I DID NOT CHANGE that industrial format. I only added two additional chunks for storing additional fractal coefficients into the RIFF container.
- "Over clocking".
Just take a simple coffee-break. Let’s imaging that a student at MIT has decided to develop decoder of MP3 format with special function – increasing output audio stream. It could be cool to have decoder which from the original encoded stream with 48000 Hz frequency can decode the output stream with 96000 Hz or ever 192000 Hz. The student has decided to increase frame of inverse Fourier transformation in 2 times. It needs to take 2 times more coefficients from encoded stream, but it is impossible – format has fixed length of frame encoding. The student has decided to put the new coefficients to zero – gets significant distortions. The student has decided to double the existence ones – gets significant distortions. The student has asked the mentor. The mentor, before kicking the student out MIT with shame, lectured long lecture about linear orthogonal transformations.
The case of problem is that it is impossible to resolve system of linear orthogonal equations if there is not full set of coefficients. You can ask – how about the developed system? In format MP3 all data are regular – they have the same meaning – frequency. However, in the developed fractal format all coefficients have different meaning. It is impossible to find the initial length of rang from the coefficients of fractal transformation. It is a problem. If a student with shame can go to work in Microsoft, we need a real solution. It is obviously that
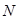 must be more than zero. It is like with the growing the crystal – you can choose the "seed" and grow up the crystal to any size. In the real world we have three limits:
must be more than zero. It is like with the growing the crystal – you can choose the "seed" and grow up the crystal to any size. In the real world we have three limits:1. Value of
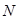 must be more or equal one — due to discretisation of signal space. It is impossible to take N with half or quarter sample's width. So, the least possible audio stream sample rate is 1 sample on rang – or the speed of audio stream for prelistening.
must be more or equal one — due to discretisation of signal space. It is impossible to take N with half or quarter sample's width. So, the least possible audio stream sample rate is 1 sample on rang – or the speed of audio stream for prelistening.
2. As it is mentioned previously – the original frame of samples is spitted by scheme of BinTree – relation between rangs is power of 2. As a result, the decoded stream can has sample rate in one, two, four, eight and more times more then sample rate of audio stream for prelistening.
3. It is obviously limitated by audio equipment.
You will ask – how is it realised in the presented project?
After opening file with fractal content panel ‘Options of 'ROAD' part’ will be enabled, and you can select comboBox – ‘Frequency of Output stream’. The list of possible frequencies for fractal file, which is encoded from the audio file with the original frequency 44100 Hz will be filled with items from 11025 Hz to 88200 Hz.

The list of possible frequencies for fractal file, which is encoded from the audio file with the original frequency 48000 Hz will be filled with items from 12000 Hz to 96000 Hz (if you are fortune on your computer the top frequency will be 192000 Hz).

You can download some audio tracks for testing this feature: Origa - Inner Universe 4Samples.road.wav, Alpha - Revolution in Paradise 32Samples.road.wav, Alpha - Revolution in Paradise 8Samples.road.wav, Alpha - Revolution in Paradise 4Samples.road.wav Attention!!! These files are based on 'WAVE' format. Your regular audio player can play it with quality of Mono channel with 12000 Hz (or 11050 Hz). Only presented in this article player can play it with the mentioned options!!! (version for Windows: Audio_Fractal_Bin.zip)
You can test the track - StepSignals.road.wav.

-
“Expanding”.
I think that many people who is reading this article know about audio standards, and know about limitation of an amount of bits per sample in audio stream. It is usually 16 bits. However, what will happened if we decide to increase its value for output audio stream? In the usually situation it is the same as increase the loud in 65536 times (it is powerful :)). You can say - just a minute, how about "Over clocking". The fact is that in the case of "Over clocking" the new samples will be synthesised in the new bit range. It means that they fill dynamic range, which was cut out in the time of recording of the original audio file!!! It can be executed in the programm by selecting option: «Output bits per sample»:
-
None-Determenated, stochastic decoding.
Firstly, each decoded frame is the union of rangs, and each rang can be processed independent in any order:

Secondly, they can have the recursion reference. It means that they can work with the same buffer, and the result of fractal transformation of one rang can be used for computing others. You can say – it leads to Chaos, but fractal transformation is based on Chaos. The fact is that each execution of fractal transformation increase similarity in signal and decrease non-similarity:

You say – OK, but the system is determinate, like any computer system. Yes, of course. For generating random numbers I use in code the random number generator from С++ 11 std library. It allows to mess order of execution of fractal transformation. It looks like to take flock of monkeys, give them the book – “Plays of Shakespeare for Dummies” and allows to tear it and link it in any order. In the case of fractal transformation – you will get the full collection of Shakespeare’ plays with author’s edition :))).
Interpretation:
Many mathematical conceptions have the physical interpretation. For instance – numeral  and a circle. It is common to find the general interpretation of the fractal transformation in the description of growing of crystals or ever trees. However, I would like to present another physical interpretation of fractal transformations.
and a circle. It is common to find the general interpretation of the fractal transformation in the description of growing of crystals or ever trees. However, I would like to present another physical interpretation of fractal transformations.
If you look at the main equation which is used in the article:

Then you can see that it can be presented in the next schema:

If it presents for each sample then we can get the next schema:

I think that many readers mark that it is very similar to the schema of artificial neuron:

transformations  and
and  are considered as functions of averaging by input,
are considered as functions of averaging by input,  - it sensitive of neuron for income signals,
- it sensitive of neuron for income signals,  - level of a bias input. The different is only in a couple details: sensitive of neuron for income signals is defined for each input, and output value is transformed by transfer function to Boolean state - step function (however, there is also a linear combination).
- level of a bias input. The different is only in a couple details: sensitive of neuron for income signals is defined for each input, and output value is transformed by transfer function to Boolean state - step function (however, there is also a linear combination).
So, what will happen if we look at fractal transformation from theory of artificial neuron network? Each samples in vector  can be considered as one artificial neuron with soft decision. In this case vector
can be considered as one artificial neuron with soft decision. In this case vector  is a layer of artificial neurons with the common properties. As a result we can make the next interpretation – transformation
is a layer of artificial neurons with the common properties. As a result we can make the next interpretation – transformation  can be considered as tracking connections between neurons. Artificial neuron network with tracking connections (topology) between neurons for each specific task – is someone heard about it? You can ask – what about other features of fractal transformations? So, I can make the next suggestions:
can be considered as tracking connections between neurons. Artificial neuron network with tracking connections (topology) between neurons for each specific task – is someone heard about it? You can ask – what about other features of fractal transformations? So, I can make the next suggestions:
- Recursion — the result of artificial neuron network has become her input, but condition of shrinking of signal makes the state of network stable after some iterations;
- Topology 'spiral' — it is possible to create spiral links between rangs-layers.

- Random selecting of sequence of the rangs for computing - stochastic interaction between layers of artificial neuron network;
- Prelistening — possibility to set the rational interpreted levels of bias input for artificial neurons.
- “Over clocking” – simple scaling of the existing artificial neuron network by simple adding new neurons in each layer-rang WITHOUT changing of configuration of the network. It results to more detailed state of the network with generation of the new details (it likes scaling of fractals image for viewing of new element).
So, what is name of it all? Recursion scaled asynchonized non-determinate artificial neuron network with tracking of topology and soft decision. is not it? How can it be used? On the pictures you can see examples of recursion application fractal transformation to image which is close to the encoded one - "Lena" (but with some distortions).



You can see that after excluding of some elements the fractal transformation can build image, very close to encoded after one iteration. However, for image "Rose" which is differ from the original one we get real “Chaos” after first iteration (more detailed information can be found in my book :)).
Summary
In this article I present some result of my working with implementation of fractal transformation in the real task - compression of audio data. I present the new technology and show the difference from the others. You can ask - if it is so cool - why is it not used? The fact is that for encoding of ONE 5 minutes track the code takes 6000 SECONS - almost TWO HOURS. It is huge time. However, I keep a hope that the problem with time consumption can be resolved - the fact is that code is compiled on MinGW. In my view it is possible to accelerate execution of code by using optimised compiler, by using SSE commands (about 2 or 3 time) and by parallel threading of code (at least 2 times). Of course, you can say that 1000 SECONDS (or about 16 minutes) for encoding of 5 minutes track is too much, but the FIVE ABOVE MENTIONED FEATURES of the new format can override it is disadvantage. It is interesting question - how much time do people spend on encoding the lovely music and how many times do people listen it with the perfect quality?
If you have got some interest about the new technique of compression of audio data - so, you can join to my project on https://github.com/Xirexel/ROAD.
UPDATE
ROADConvertor
I updated the project of ROAD and added the ROADConvert util.
I wrote about the stack structure of the new format, which is used in the project and it is presented there:

The schema presents the mentioned ideas: the top element is a fractal compression algorithm - ROAD, the middle element is manager level for pack-unpack fractal coefficient and execution entropy compression, the bottom element is level for processing of storing in the file - at the present time it is a WAVE format. As a result, the developed stack has name ROADoverWAVE.
I developed more simple programm for converting WAVE format files into the ROAD format. The interface of it is presented on the next two images:


You can see that the programm is more friendly for user. The files for encoding can be added by pushing the button "Add files" or just by drag-and-drop of the original WAVE format files. The type of stack of encoding can be selected from the combobox - by default it is ROADoverWAVE stack format. Encoding of each audio track is executed in the seperated thread - it leads to multithreading processing of data. The workable programm for Windows platform can be found on link - ROADConvertor. The code can be found in my project on https://github.com/Xirexel/ROAD or the release can be downloaded on link - ROAD-v0.0.1.zip. The encoded files of ROAD fromat is stored into the Document folder.
Winamp input ROAD plugin
So, embedded player for the format - it is OK, but how it can work with the real audio player? I wrote simple input plugin for Winamp player which can now play the new developed ROAD fromat - Download Winamp in_road-noexe.zip plugin. For using the plugin, it is enough to take it from the ZIP file and put it into Plugins folder of the Winamp player. The code of the plugin can found on my GitHub repository - WinampPlugin_in_road. The zip release can be downloaded on link - WinampPlugin_in_roadv0.0.zip. Working with the in_road plugin is presented on the next two images:


You can see from the last image that the decoded track is played with the unusual byte speed - about 10 Mbyte/c and sample frequency - 176 kHz!?! The answer can be found from the below code:
lsamplesPerRang = 1;
lNewSampleRate = globalROADoverWAVEproxy.sampleRate;
lOutBPS = lBPS;
lChannels = globalROADoverWAVEproxy.fractalFormat._originalAmountOfChannels;
if(lBPS == 16)
lOutBPS = 32;
for(lSampleRate = lNewSampleRate;
lSampleRate <= globalMaxSampleRate;
lSampleRate = lsamplesPerRang * globalROADoverWAVEproxy.sampleRate)
{
int res = mod.outMod->Open(lSampleRate,lChannels,lOutBPS, -1,-1);
if(res >= 0)
{
lNewSampleRate = lSampleRate;
result = 0;
}
lsamplesPerRang *= 2;
mod.outMod->Close();
}
lsamplesPerRang = lNewSampleRate / globalROADoverWAVEproxy.sampleRate;
globalROADoverWAVEproxy.openFile(fn, lsamplesPerRang, globalROADoverWAVEproxy.fractalFormat, lBPS, lOutBPS, &globalROADoverWAVEproxy._ptrIReader);
The code enumerates all accesseble values of the Winamp output driver and finds the most top options of the output driver for increase value of the lsamplesPerRang for scaling up of the decoded sample rate.
History
25.10.2014 - add references on ROADConvertor and Winamp input ROAD format plugin.
