Symbolic Differentiation
4.89/5 (335 votes)
This article demonstrates differentiating expressions using a stack and displaying the input expression and its derivative.
Contents
- Introduction
- Differentiation Definition
- Mathematical Expression
- Differentiation Steps
- Differentiation Pseudo Code
- Program Tabs
- Points of Interest
- Updates
- References
- License
Introduction
In this article, I describe how we can parse a mathematical expression and identify its elements. I chose a simple application of a symbolic differentiation as an example, to add more value to the article and to give maximum benefit to the readers. The application, as in the previous figure, includes a simple grid to draw an input curve and its differentiation in the same view. I will not dig into the mathematics, as that is out of the article scope. I will just include a definition of the derivative in the next section. If you are not interested in the math, you can skip it.
Differentiation Definition
The derivative of a function can be interpreted either as a function whose value at x is equal to the gradient of the tangent line to the graph of y=f(x) at x, or, alternatively, as a function that describes the instantaneous rate of change of y with respect to x at the point x. The derivative of f with respect to x can also be denoted by:
d(f(x))/dx,
or if y = f(x), dy/dx
Differentiation Formulas
| Serial | Expression | Derivative | Remarks |
u+v |
du/dx+dv/dx |
||
u-v |
du/dx-dv/dx |
||
u/v |
(v*du/dx-u*dv/dx)/v^2 |
||
u*v |
u*dv/dx+v*du/dx |
||
c*u |
c*du/dx |
c is constant |
|
u^v |
v*u^(v-1)*du/dx+u^v*ln(u)*dv/dx |
||
u^n |
n*u^(n-1)*du/dx |
n is real |
|
c^u |
c^u*ln(c)*du/dx |
c is constant |
|
e^u |
e^u*du/dx |
e = 2.7182818284590452353602874713527 |
|
| 1 | sin(u) |
cos(u)*du/dx |
|
| 2 | cos(u) |
-sin(u)*du/dx |
|
| 3 | tan(u) |
sec(u)^2*du/dx |
|
| 4 | sec(u) |
sec(u)*tan(u)*du/dx |
|
| 5 | cosec(u) |
-cosec(u)*cot(u)*du/dx |
|
| 6 | cot(u) |
-cosec(u)^2*du/dx |
|
| 7 | sinh(u) |
cosh(u)*du/dx |
|
| 8 | cosh(u) |
sinh(u)*du/dx |
|
| 9 | tanh(u) |
sech(u)^2*du/dx |
|
| 10 | sech(u) |
sech(u)*tanh(u)*du/dx |
|
| 11 | cosech(u) |
cosech(u)*coth(u)*du/dx |
|
| 12 | coth(u) |
-cosech(u)^2*du/dx |
|
| 13 | asin(u) |
1/sqrt(1-u^2)*du/dx |
|
| 14 | acos(u) |
-1/sqrt(1-u^2)*du/dx |
|
| 15 | atan(u) |
1/(1+u^2)*du/dx |
|
| 16 | asec(u) |
1/(|u|*sqrt(u^2-1))*du/dx |
|u| is abs(u) |
| 17 | acosec(u) |
-1/(|u|*sqrt(u^2-1))*du/dx |
|u| is abs(u) |
| 18 | acot(u) |
-1/(1+u^2)*du/dx |
|
| 19 | asinh(u) |
1/sqrt(u^2+1)*du/dx |
|
| 20 | acosh(u) |
1/sqrt(u^2-1)*du/dx |
|
| 21 | atanh(u) |
1/(1-u^2)*du/dx |
|
| 22 | asech(u) |
-1/(u*sqrt(1-u^2))*du/dx |
|
| 23 | acosech(u) |
-1/(u*sqrt(1+u^2))*du/dx |
|
| 24 | acoth(u) |
1/(1-u^2)*du/dx |
|
| 25 | sqrt(u) |
1/(2*sqrt(u))*du/dx |
|
| 26 | log10(u) |
1/(u*ln(10))*du/dx |
|
| 27 | log(u) |
1/u*du/dx |
|
| 28 | ln(u) |
1/u*du/dx |
|
| 29 | sign(u) |
0 |
|
| 30 | abs(u) |
u/|u|*du/dx |
|u| is abs(u) |
Mathematical Expression
A mathematical expression includes numbers, operators, functions, variables and operators. Operators include +, -, *, / and ^. Functions are like sin(x) and variables are like x. Our target here is to identify each element and to get the right differentiation rule applied to that element or a group of elements.
Expression examples:
sin(2*x)/x
sin(45+cos(2)/tan(x)
sign(cos(x)
32*9-8/2
Differentiation Steps
Expression Parsing to Fill Stack
Expression parsing is the process of scanning an expression to find its elements (numbers, operators, functions and variables). Each operator should have two operands; for example, take 2*12. The operator "*" has two operands: 2 and 12. Each function has its argument. For example, for sin(x), the function is sin and the argument is x. So, we should scan the expression in a specific way to identify each operator and the operands, as well as each function argument, to simplify the calculation or the differentiation.
Expression execution depends on operator precedence. If we can construct a stack of operators and operands such that each operator is followed by its two operands, 2*12 should construct this stack: "*, "2", "12". So, the calculation function checks the stack. If the item is an operator, then it takes its two operands and does the calculation for them in a recursion formula, so the whole expression can be calculated. For example, the expression:
sin(2*12)/7+9^2
...should be calculated in these steps:
- Calculate
sin(2*12)/7 - Calculate
9^2 - Then apply the operator
+for the two results - To calculate point 1, we need to:
- Calculate
sin(2*12) - Calculate 7
- Then divide the two results
- To calculate point 4.1, we need to:
- Calculate
2*12 - Apply the
sinfunction to the result - To calculate point 4.4.1, we need to:
- Apply the operator
*to the two operands 2 and 12
- Apply the operator
- Calculate
- Calculate
The function that does the scanning takes the input expression and an array of operands depending on their precedence, as in the following code:
///////////////////////////////////////////////////////////
// GetOperator: scan the input string
// to search for any of the input operators
///////////////////////////////////////////////////////////
int GetOperator(IN LPCSTR lpcs, IN LPCSTR lpcsOperators[])
{
for(int nIndex = 0; lpcsOperators[nIndex]; nIndex++)
{
int nOpen = 0;
// scan the expression from its end
LPSTR p = (LPSTR)lpcs+strlen(lpcs)-1;
// loop tells reach expression start
while(p >= lpcs)
{
// check for close
if(*p == ')')
nOpen++;
// check for open
else if(*p == '(')
nOpen--;
// check for operator
else if(nOpen == 0 && strchr(lpcsOperators[nIndex], *p) != NULL)
// check if the operator in not a sign mark
if((*p != '-' && *p != '+') ||
(p != lpcs && IsRightSign(*(p-1),
lpcsOperators, nIndex+1)))
// return operator index
return (int)(p-lpcs);
p--;
}
}
// operator not found
return -1;
}
It is obvious now that it is a recursion operation. To do that, we need to formulate the expression in a stack of operators and operands, and process that stack in a certain way to get the final result. The main steps to do that in brief are:
- Find operators
- Split the expression at the operator index
- Add the two resultant operands to the stack
- If operators are not found, then check if the expression starts with a function name
If we apply the previous steps, we will have the stack in this form:
| + | ||||
| / | ||||
| sin(2*12) |
|
|||
| 7 | ||||
| ^ | ||||
| 9 | ||||
| 2 |
To describe that in more detail, let us have a look at the code that parses the expression and fills the stack:
bool FillStack(LPCSTR lpcsInput, vector<EXPRESSIONITEM*>& vStack)
{
// operators array from high to low
priority LPCSTR lpcsOperators[] = { "+-", "*/", "^%", NULL };
// insert first input into the stack
vStack.push_back(new ExpressionItem(lpcsInput));
// loop in Expression stack to check if
// any Expression can be divided to two queries
for(int nIndex = 0; nIndex < (int)vStack.size(); nIndex++)
// check if Expression item is operator
if(vStack[nIndex]->m_cOperator == 0)
{
// copy Expression string
CString str = vStack[nIndex]->m_strInput;
// parse expression to find operators
int nOpIndex = GetOperator(str, lpcsOperators);
if(nOpIndex != -1)
{
// split the Expression into
// two queries at the operator index
vStack[nIndex]->m_cOperator = str[nOpIndex];
// add the left operand of the
// operator as a new expression
vStack.insert(vStack.begin()+nIndex+1,
new ExpressionItem(str.Left(nOpIndex)));
// add the right operand
// of the operator as a new expression
vStack.insert(vStack.begin()+nIndex+2,
new ExpressionItem(str.Mid(nOpIndex+1)));
}
else
// check if Expression string
// starts with function or parenthesis
if((vStack[nIndex]->m_nFunction = GetFunction(str,
vStack[nIndex]->m_nSign)) == 0
&& vStack[nIndex]->m_nSign == 0)
// remove parentheses and re-scan the Expression
vStack[nIndex--]->m_strInput =
str.Mid(1, str.GetLength()-2);
}
return true;
}
No one can ever deny now that this is the simplest code you can find about mathematical expression parsing. We can collect its comments in points, as follows:
- Insert the first input into the stack
- Loop in the expression stack to check if any expression can be divided into two queries
- Check if the expression item is an operator (+-*/^)
- Parse the expression to find the operators
- If an operator is found:
- Split the expression into two queries at the operator index
- Add the left operand of the operator as a new expression
- Add the right operand of the operator as a new expression
- Else
- Check if the expression string starts with a function or a parenthesis
- If a function is found, set its number in the expression data
Apply Differentiation Formulas on the Stack
Applying differentiation formulas means to iterate the stack, take each operator and apply the differentiation rule - depending on the operator - on the two operands of the operator:
| Expression | Derivative |
u+v |
du/dx+dv/dx |
u-v |
du/dx-dv/dx |
u/v |
(v*du/dx-u*dv/dx)/v^2 |
u*v |
u*dv/dx+v*du/dx |
c*u |
c*du/dx |
u^n |
n*u^(n-1)*du/dx |
c^u |
c^u*ln(c)*du/dx |
e^u |
e^u*du/dx |
If any operand is an operator, then the function is called again in a recursive way to differentiate the whole expression. The following code represents this function:
CString DifferentiateStack(vector<EXPRESSIONITEM*>& vStack, int& nExpression)
{
ExpressionItem *pQI = vStack[nExpression++];
if(pQI->m_cOperator)
{
// get left operand
CString u = vStack[nExpression]->GetInput();
// get left operand differentiation
CString du = DifferentiateStack(vStack, nExpression);
// get right operand
CString v = vStack[nExpression]->GetInput();
// get right operand differentiation
CString dv = DifferentiateStack(vStack, nExpression);
if(du == '0') // u is constant
...
else if(dv == '0') // v is constant
...
else
switch(pQI->m_cOperator)
{
case '-': // d(u-v) = du-dv
case '+': // d(u+v) = du+dv
pQI->m_strOutput = '('+du+pQI->m_cOperator+dv+')';
break;
case '*': // d(u*v) = u*dv+du*v
pQI->m_strOutput = '('+u+'*'+dv+'+'+du+'*'+v+')';
break;
case '/': // d(u/v) = (du*v-u*dv)/v^2
pQI->m_strOutput = '('+du+'*'+v+'-'+u+'*'+dv+")/("+v+")^2";
break;
case '^': // d(u^v) = v*u^(v-1)*du+u^v*ln(u)*dv
pQI->m_strOutput = '('+v+'*'+u+"^("+v+"-1)*"+ du+
'+'+u+'^'+v+"*ln("+u+")*"+dv+')';
break;
}
}
else
// get Expression differentiation
pQI->GetDifferentiation();
// return resultant differentiation
return pQI->m_strOutput;
}
Optimize Equation
Optimizing the equation includes these simple steps:
- Replace "--" with "" or "+"
- Replace "+-" with "-"
- Replace "((....))" with "(....)"
- Remove any "1*"
- Remove any "*1"
- Remove any "^1"
- Remove any "1*"
- Remove unneeded parentheses
Differentiation Pseudo Code
Differentiate(input)
{
Stack = FillStack(input)
output = DifferentiateStack(Stack)
Optimize(output)
return output
}
FillStack(input)
{
operators[] { "+-", "*/", "^%" }
stack.push(input)
loop( n = 1 to stack.size() )
{
if stack[n] is not operator
if GetOperator(stack[n],
operators) success
{
Split stack[n]
stack.Insrt(left operand)
stack.Insrt(right operand)
}
else
GetFunction(stack[n])
}
}
DifferentiateStack(stack, index)
{
if stack[index] is operator
{
index++
u = stack[index]
du = DifferentiateStack(stack, index)
v = stack[index]
dv = DifferentiateStack(stack, index)
if operator = '-' or '+'
output = du+operator+dv
else if operator = '*'
output = u*dv+du*v
else if operator = '/'
output = (du*v-u*dv)/v^2
else if operator = '^'
output = v*u^(v-1)*du+u^v*ln(u)*dv
}
else
output = stack[index++].GetDifferentiation()
return output
}
void Optimize(str)
{
replace "--" with "" or "+"
replace "+-" with "-"
replace "((....))" with "(....)"
remove any 1*
remove any *1
remove any exponent equal 1
remove unneeded parentheses
if str changed then
Optimize(str)
}
ExpressionItem::GetDifferentiation()
{
if Function then
{
arument = Argument(input);
if function = SIN
output = Differentiate(arument)*cos(arument)
else if function = COS
output = Differentiate(arument)*(-sin(arument))
else
...
}
}
else
{
if input = "x"
output = "1"
else if input = "-x"
output = "-1"
else if input is numeric
output = "0"
else
output = "d"+input+"/dx"
}
}
Program Tabs
Differentiation
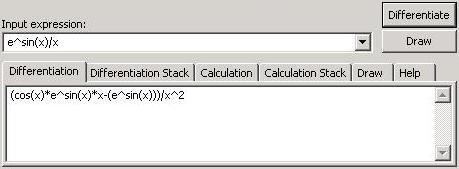
The Differentiation tab displays the differentiation results after applying the differentiation steps in the input expression. The input expression is calculated before differentiation to optimize any arithmetic part that includes numbers as in the example:
e^sin(pi/3)/tan(x) is optimized to 2.377442/tan(x) before differentiation to get the result (-2.377442*sec(x)^2)/(tan(x))^2.
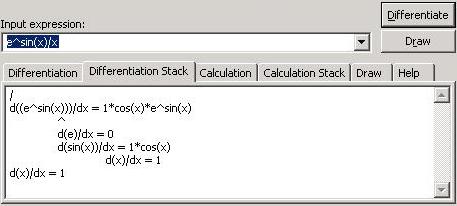
Differentiation Stack
Calculation
This tab is a Symbolic Calculator that can calculate any mathematical expression, however complicated. The calculation includes only two constants:
e = 2.7182818284590452353602874713527
pi = 3.1415926535897932384626433832795

Calculation Stack
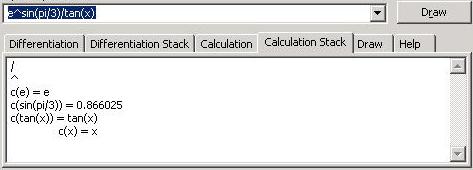
This view is used to view the stack of the calculation details. c( ) means "the calculation of." The stack contents are arranged from top to bottom. Calculation steps are differentiation steps, except the operators' formulas. The advantage of this view is that it enables showing of the parts that can be calculated in the expression and those that can't be calculated, as in the example in the figure.
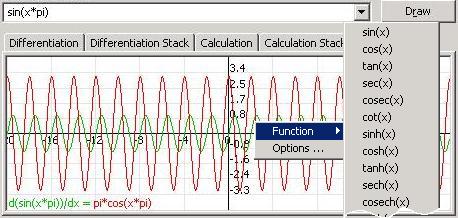
Draw
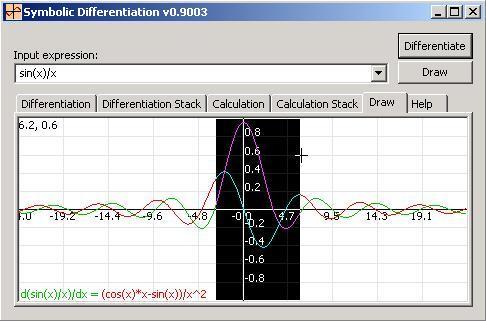
This tab is used to view the input function curve and its differentiation curve. You can view the input function curve only by clicking "Draw." The view includes horizontal and vertical axes, as well as grid lines. You move over any point in the view to see its coordinates in the left upper corner, and you can zoom in on any part by selecting it with the mouse. The horizontal and vertical axes' limits update automatically to include the input function points in the view. You can change these limits by right clicking the view.
Help
This tab just displays a list of allowed functions in the application.
Points of Interest
- Part of Expression Calculation
The advantage of my expression parsing over other parsers on the net is that it can calculate part of the expression and leave the other part, and that includes any variables. For example, take the expression
sin(45+sin(2))/tan(x). If you try to input this expression to any free parser on the net, it will give an error indicating an invalid characterx. However, my parser gives you0.937227/tan(x). For any complex expression, my parser tries to optimize the expression before the differentiation, and calculates any part that can be calculated. So, the differentiation ofsin(45+sin(2))/tan(x)is(-0.937227*sec(x)^2)/(tan(x))^2. - Operator Precedence
When a complex expression has multiple operators, the operator precedence determines the sequence in which the operations are performed. The order of execution can significantly affect the resulting value. Operators have these precedence levels. An operator on higher levels is evaluated before an operator on a lower level:
- + (Positive), - (Negative)
- ^ (Exponent), % (Modulo)
- * (Multiply), / (Division)
- + (Add), - (Subtract)
When two operators in an expression have the same operator precedence level, they are evaluated left to right based on their position in the expression. For example, in
4 - 2 + 27, the subtraction operator is evaluated before the addition operator to get2 + 27, which yields an expression result of29.Use parentheses to override the defined precedence of the operators in an expression. Everything within the parentheses is evaluated first to yield a single value before that value can be used by any operator outside of the parentheses. For example,
2 * 4 + 5evaluates to8 + 5, which yields an expression result of13. The expression2 * (4 + 5)evaluates to2 * 9; the parentheses cause the addition to be performed first and so the expression result is 18.If an expression has nested parentheses, the most deeply nested expression is evaluated first. The example
2 * (4 + (5 - 3) )contains nested parentheses, with the expression5 - 3in the most deeply nested set of parentheses. This expression yields a value of2. Then the addition operator (+) adds this result to4, which yields a value of6. Finally, the6is multiplied by2to yield an expression result of12. - Zoom In
In the drawing area, you can select any area to zoom in on. For example, the function
sin(100*x)has a very large variation, as in the following figure:
By zooming in many times, we can view the smaller details, as in the following figures:



Note: Check the horizontal axis resolution after each zoom-in.
Updates
- v0.9001: Added error checking for function arguments
- v0.9002: Added exponent derivative and some equation optimization,
d(u^v) = v*u^(v-1)*du+u^v*ln(u)*dv - v0.9003: Solved the bug of incorrect definitions for the
sec,cosec,sechandcosechfunctions - v0.9004: Added software license section
- v0.9005: d(cosh(x))/dx = sinh(x) thanks to 'Mike O'Neill'
- v0.9006: Corrected the calculation of the atan function thanks to 'Kevin'
- v0.9007: Adjusted equation optimization function. Thanks to 'Kevin'
- v0.90071: [5-03-2008] Adjusted equation optimization function. Thanks to 'Kevin'
References
- Advanced Mathematics for Engineers and Scientists, by Murray R. Spiegel, Ph.D. 1983 (Differentiation Formulas)
- Microsoft Developer Network (Operator Precedence)
