Towers of Hanoi Puzzle Simulation
2.71/5 (6 votes)
The article describes a recursive solution for the famous puzzle of the towers of Hanoi
Introduction
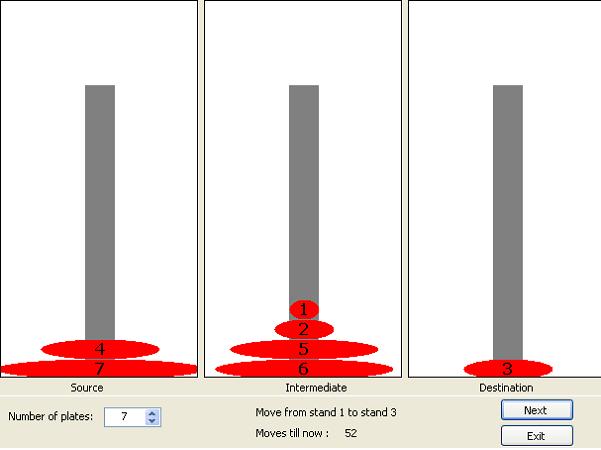
The Tower of Hanoi or Towers of Hanoi is a mathematical game or puzzle. It consists of three stands, and a number of plates of different sizes which can be put over each other on any stand.
The puzzle starts with the plates stacked in order of size on one stand we call source, smallest at the top, making a pyramidshape.
The object of the game is to move the entire stack to another stand (destination), obeying the following rules:
- Only one disc may be moved at a time.
- No disc may be placed on top of a smaller disc.
Solution
Recursive Algorithm
- Label the stands Src, Intr, Dest.
- Let n be the total number of discs.
- Number the discs from 1 (smallest, topmost) to n (largest, bottommost).
To move n discs from stand Src to stand Dest:
- Move n-1 plates from Src to Intr. This leaves plate #n alone on plate Src.
- Move plate #n from Src to Dest.
- Move n-1 plates from Intr to Dest so they sit on plate #n.
The above is a recursive algorithm: to carry out steps 1 and 3, apply the same algorithm again for n-1. The entire procedure is a finite number of steps, since at some point the algorithm will be required for n = 1. This step, moving a single plate from stand Src to stand Dest, is trivial.
The Tower of Hanoi is a problem often used to teach beginning programming, in particular as an example of a simple recursive algorithm. It is also an example of an exponential time algorithm — for all but the smallest number of discs, it will take an impractically huge amount of time, even on the fastest computers in the world. There is no way to improve on this, because the minimum number of moves required to solve the puzzle is exponential in the number of plates, which is 2n - 1, calculated by using recurrence relations, where n is the number of plates.
Code
SolveTowers()
// code for the recursive method
// count are number of plates,
// source stand, destination stand and intermediate stand
private void SolveTowers(int count, int source, int dest, int inter)
{
if (count == 1)
{
MoveFromTo(source, dest);//To Draw the action performed
TotalMoves++; //keep track of number of moves
}
else
{
//1- Move n-1 from source to intermediate stand using destination as a
//spare
solveTowers(count - 1, source, inter, dest);
//2-Move plate #n from Src to Dest
solveTowers(1, source, dest, inter);
//3-Move n-1 plates from intermediate to dest so they sit on plate #n
solveTowers(count - 1, inter, dest, source);
}
}
Reference
History
- 12th July, 2006: Initial post
