2D Polygon Collision Detection
4.77/5 (52 votes)
An article on polygon collision detection. Can be used to implement collision between sprites in a 2D game. The algorithm can also be extended to 3D.

Introduction
This article describes how to detect the collision between two moving (2D) polygons. It's not the first tutorial on the topic, however, the tutorials on the net tend to be a bit too complex for a relatively simple problem. The source codes I could find also had too many abbreviations that I don't get, or were crippled with C optimizations. So here, I'll try to keep it as simple as possible. In any case, it should be possible to include the functions presented here to your C# projects quite straightforwardly. The technique can be used to detect collisions between sprites as an alternative to pixel-perfect collisions which are usually too slow.
Background
To detect if two polygons are intersecting, we use the Separating Axis Theorem. The idea is to find a line that separates both polygons - if such a line exists, the polygons are not intersecting (Fig. 1). The implementation of this theorem is relatively simple, and could be summed up in this pseudo code:
- For each edge of both polygons:
- Find the axis perpendicular to the current edge.
- Project both polygons on that axis.
- If these projections don't overlap, the polygons don't intersect (exit the loop).
This can be easily extended to deal with moving polygons by adding one additional step. After having checked that the current projections do not overlap, project the relative velocity of the polygons on the axis. Extend the projection of the first polygon by adding to it the velocity projection (Fig. 2). This will give you the interval spanned by the polygon over the duration of the motion. From there, you can use the technique used for static polygons: if the projections of polygons A and B don't overlap, the polygons won't collide. (NB: However, remember that if the intervals do overlap, it doesn't necessarily mean that the polygons will collide. We need to do the test for all the edges before knowing that.)
Once we have found that the polygons are going to collide, we calculate the translation needed to push the polygons apart. The axis on which the projection overlapping is minimum will be the one on which the collision will take place. We will push the first polygon along this axis. Then, the amount of translation will simply be the amount of overlapping on this axis (Fig. 3).
That is it! Now, each time a collision occurs, the first polygon will nicely slide along the surface of the other polygon.

Figure 1: Projections of the polygons onto an axis.
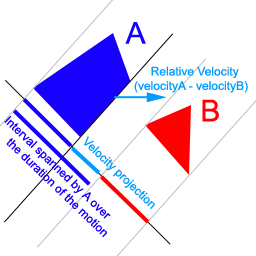
Figure 2: Projections for moving polygons.
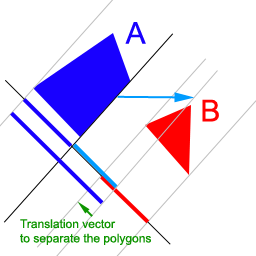
Figure 3: Find the minimum interval overlapping, then calculate the translation required to push the polygons apart.
Using the code
The PolygonCollision() function does all of the above, and returns a PolygonCollisionResult structure containing all the necessary information to handle the collision:
// Structure that stores the results of the PolygonCollision function
public struct PolygonCollisionResult {
// Are the polygons going to intersect forward in time?
public bool WillIntersect;
// Are the polygons currently intersecting?
public bool Intersect;
// The translation to apply to the first polygon to push the polygons apart.
public Vector MinimumTranslationVector;
}
Two helper functions are used by the PolygonCollision function. The first one is used to project a polygon onto an axis:
// Calculate the projection of a polygon on an axis
// and returns it as a [min, max] interval
public void ProjectPolygon(Vector axis, Polygon polygon,
ref float min, ref float max) {
// To project a point on an axis use the dot product
float dotProduct = axis.DotProduct(polygon.Points[0]);
min = dotProduct;
max = dotProduct;
for (int i = 0; i < polygon.Points.Count; i++) {
dotProduct = polygon.Points[i].DotProduct(axis);
if (d < min) {
min = dotProduct;
} else {
if (dotProduct> max) {
max = dotProduct;
}
}
}
}
The second one returns the signed distance between two given projections:
// Calculate the distance between [minA, maxA] and [minB, maxB]
// The distance will be negative if the intervals overlap
public float IntervalDistance(float minA, float maxA, float minB, float maxB) {
if (minA < minB) {
return minB - maxA;
} else {
return minA - maxB;
}
}
Finally, here is the main function:
// Check if polygon A is going to collide with polygon B.
// The last parameter is the *relative* velocity
// of the polygons (i.e. velocityA - velocityB)
public PolygonCollisionResult PolygonCollision(Polygon polygonA,
Polygon polygonB, Vector velocity) {
PolygonCollisionResult result = new PolygonCollisionResult();
result.Intersect = true;
result.WillIntersect = true;
int edgeCountA = polygonA.Edges.Count;
int edgeCountB = polygonB.Edges.Count;
float minIntervalDistance = float.PositiveInfinity;
Vector translationAxis = new Vector();
Vector edge;
// Loop through all the edges of both polygons
for (int edgeIndex = 0; edgeIndex < edgeCountA + edgeCountB; edgeIndex++) {
if (edgeIndex < edgeCountA) {
edge = polygonA.Edges[edgeIndex];
} else {
edge = polygonB.Edges[edgeIndex - edgeCountA];
}
// ===== 1. Find if the polygons are currently intersecting =====
// Find the axis perpendicular to the current edge
Vector axis = new Vector(-edge.Y, edge.X);
axis.Normalize();
// Find the projection of the polygon on the current axis
float minA = 0; float minB = 0; float maxA = 0; float maxB = 0;
ProjectPolygon(axis, polygonA, ref minA, ref maxA);
ProjectPolygon(axis, polygonB, ref minB, ref maxB);
// Check if the polygon projections are currentlty intersecting
if (IntervalDistance(minA, maxA, minB, maxB) > 0)\
result.Intersect = false;
// ===== 2. Now find if the polygons *will* intersect =====
// Project the velocity on the current axis
float velocityProjection = axis.DotProduct(velocity);
// Get the projection of polygon A during the movement
if (velocityProjection < 0) {
minA += velocityProjection;
} else {
maxA += velocityProjection;
}
// Do the same test as above for the new projection
float intervalDistance = IntervalDistance(minA, maxA, minB, maxB);
if (intervalDistance > 0) result.WillIntersect = false;
// If the polygons are not intersecting and won't intersect, exit the loop
if (!result.Intersect && !result.WillIntersect) break;
// Check if the current interval distance is the minimum one. If so store
// the interval distance and the current distance.
// This will be used to calculate the minimum translation vector
intervalDistance = Math.Abs(intervalDistance);
if (intervalDistance < minIntervalDistance) {
minIntervalDistance = intervalDistance;
translationAxis = axis;
Vector d = polygonA.Center - polygonB.Center;
if (d.DotProduct(translationAxis) < 0)
translationAxis = -translationAxis;
}
}
// The minimum translation vector
// can be used to push the polygons appart.
if (result.WillIntersect)
result.MinimumTranslationVector =
translationAxis * minIntervalDistance;
return result;
}
The function can be used this way:
Vector polygonATranslation = new Vector();
PolygonCollisionResult r = PolygonCollision(polygonA, polygonB, velocity);
if (r.WillIntersect) {
// Move the polygon by its velocity, then move
// the polygons appart using the Minimum Translation Vector
polygonATranslation = velocity + r.MinimumTranslationVector;
} else {
// Just move the polygon by its velocity
polygonATranslation = velocity;
}
polygonA.Offset(polygonATranslation);
Reference
History
- September 13, 2006: First version.
- September 14, 2006: Minor changes, and added the Reference section.
