Universal Framework for Science and Engineering - Part 8: Digital Image Processing

• Download source code - 2,159.3 KB
• Download installer - 1,602.0 KB
• Download documentation - 2,066.5 KB
• Download sample of local transformation - 637.5 KB
• Download sample of nonlocal transformation - 374.5 KB
• Download sample of 2D visualization of physical phenomenon - 3.6 KB
• Download sample of image graph piecewise-linear approximation - 23.9 KB
• Download sample of image graph polynomial approximation - 23.6 KB
• Download processing of oscillogram 162.1 - KB
• Download sample of Videonavigation - 18.2 KB
• Download sample of 3D Shapes 38.9 - KB

Useful links:

• Universal Science and Engineering Framework homepage
• Project AstroFrame homepage

Contents

• Introduction
• Background
• Local Processing
• Nonlocal Processing
• 2D Visualization of Physical Phenomena
• Determination of Math Dependency
• Processing of Oscilloscope Image
• Videonavigation
• Points of Interest
• History

Introduction

Digital image processing is one of the most important engineering problems. I'll not describe its applications, since you can find them here. This framework may solve lots of kinds of image processing problems. Inclusion of image processing to the framework gives several advantages. For example, image processing may be applicable to determination of the 6D position of a 3D object by photos. Latest tasks require contours of 2D images of 3D shapes. The picture at the beginning of this article is such a contour obtained by image processing.

Background

Lots of methods of image processing are based on the following principle. The color of an image pixel is the result of a calculation. The data-in of this calculation are the colors of a source image. There exist two types of processing. The first one is local, where the color of a pixel in the destination image depends on the corresponding color of one pixel in the source image only. In the second case, that of nonlocal processing, the color of a destination pixel depends on neighboring source pixels. Let' s consider these two types of processing.

Local Processing

The scheme of local processing is presented below:

This picture describes two images. Lady Rose is a source image and Lady Blue is the destination one. Other squares are math transformations. The ladies are presented below:

According to my software functionality, the result of the transformation does not only depend on the color of the pixels of the source image. It also depends on the coordinates of the pixels. So, the color of the faces and hands of both ladies are equal.

• Click here to download this sample - 637.5 KB

Nonlocal Processing

Nonlocal processing is more science-intensive than local. For example, it is used for face detection. I've used it for determination of the 6D position of a 3D object by photos. Now I'll present the Sobel gradient method. The scheme is presented below:

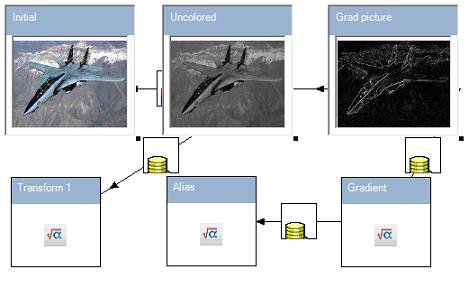
This scheme contains cascade transformations of images from Initial to Uncolored and then to Grad picture. These three pictures are presented below:

• Click here to download this sample - 374.5 KB

2D Visualization of Physical Phenomena

This section does not directly relate to image processing. Sometimes we need a 2D visualization of a physical phenomenon. Data processing of the framework enables us to do this. The picture below is a representation of one phenomenon related to optical fibers:

• Click here to download this sample - 3.6 KB

Determination of Math Dependency

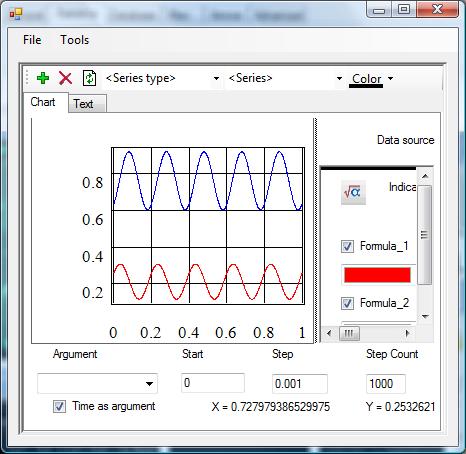
The true purpose of the framework is more the application of image processing to engineering tasks than pure image processing. Let us consider typical tasks in this area. Suppose that we have a dirty picture of a graph and we would like to build math dependency. This situation is presented in the following picture.

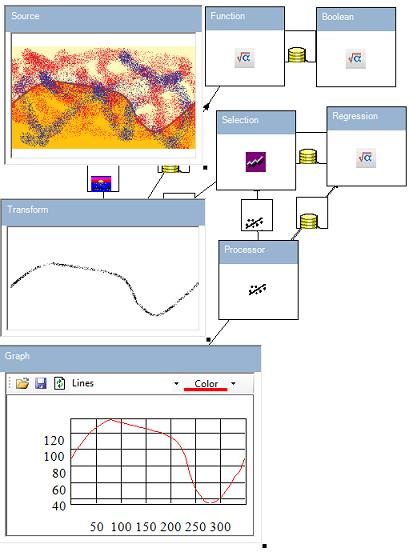
The Source picture is a bad image of math dependency. The Transform is a result of image transformation. The Selection component makes two selections from the Transform image. The first selection is a collection of black points in x-coordinates and the second one is a collection of y-coordinates. Using the regression (see Part 2) component Processor, we've processed these selections and obtained an approximation of the graph by a piecewise-linear function.

• Click here to download this sample 23.9 KB

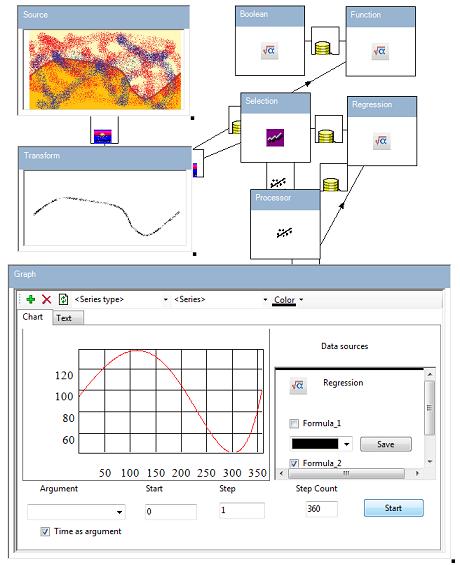
An example of an approximation graph by polynomials is presented in the following picture:

• Click here to download this sample 23.6 KB

Processing of Oscilloscope Images

Let us consider a more complicated example. Suppose we have the following oscillogram photo:

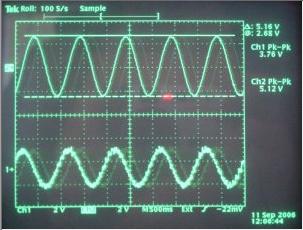
We would like to obtain the math formulas of the sine graphs, but the photo is not ideal. Moreover, axes of coordinates are not strongly horizontal and vertical. First of all, local and nonlocal processing should been applied. The brief results are presented in the following picture:

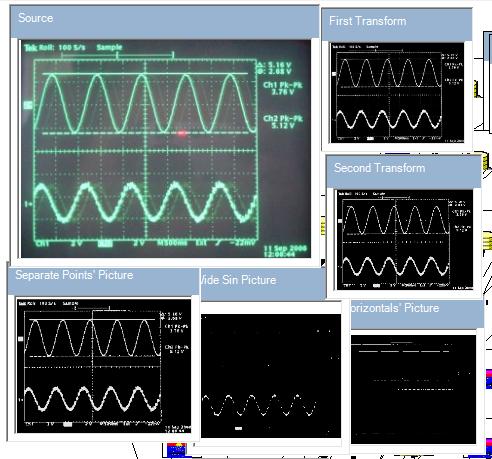
Lots of processing was left outside this picture. At last, pure sine functions and frame lines were obtained:

Then, using vertical and horizontal lines, we can obtain math parameters of border parallelograms. After this work, we can obtain a true math model of sine functions. The definition of parallelogram and sine parameters have been performed by regression (see Part 2). The result is presented in the following picture:

We had supposed that both the width and height of the border parallelogram were equal to 1.

• Download this sample - 162.1 KB

Videonavigation

If we have several sets of photos of a 3D object, we can obtain its 6D position. In this example, this problem is solved in the following way. From the photos and virtual cameras, we obtain the contours of the object as it is presented on the following picture:

The red contour corresponds to the photo. Then we perform virtual 6D motion of the object to match contours to the 3D image. In result, we have a match that looks like this:

For solving this problem, we shall use the following combination of components:

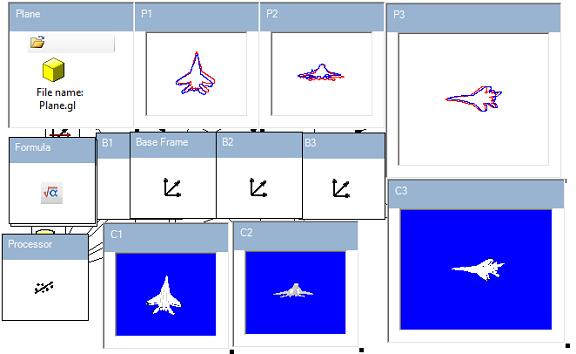
The regression component (Part 2) has been used for resolving this problem.

• To try this sample, you should download and install 3D models - 38.9 KB
• Download this sample - 18.2 KB

Points of Interest

True art has a single way. Sometimes I think that the code of good developers is my own. I was a student of the VDI Software Engineering Training Center and I could not distinguish my code from the code of other students. Similar situations arise in other branches of art. Any deformation of a Greek statue made it ugly, although this statue remains magnificent even when it left its hands. Any error of an excellent pianist is a shock for the audience. Recently, I read a book written by Gaius Julius Caesar and found that military art also has a single way. Public policy is also a kind of art. Errors of political figures lead to the shock of civilians. After many years of development, I've found that my framework has only a single way. I encountered errors along the way; however, I should inevitably correct these errors.

History

• 24 January, 2007 -- Original version posted
• 16 November, 2007 -- Article content and downloads updated