Art Gallery Problem: polygon triangulation & 3-coloring
3.78/5 (8 votes)
May 4, 2007
3 min read
64006
2581
This is a solution implementation to the well-known art gallery problem using polygon triangulation and 3-coloring methods

Introduction
From Wikipedia
The art gallery problem or museum problem is a well-studied visibility problem in computational geometry. The motivation for the problem is the real-world problem of guarding an art gallery with the minimum number of security cameras that can each rotate to obtain a full field of vision. In the computational geometry version of the problem the layout of the art gallery is represented by a simple polygon and each security camera is represented by a point in the polygon. A set S of points is said to guard a polygon if, for every point p in the polygon, there is some
such that the line segment between p and q does not leave the polygon.
As in my computational-graphics course, I was requested to implement a solution program to the art gallery problem stated above. So using cut-ear triangulation and 3-coloring algorithms, I did implement the above program in screenshot.
Background
The reader needs to have basic knowledge of computational-geometry (polygons, points, etc..)
Theory
Two-Ears
A principal vertex pi of a simple polygon P is called a ear if the diagonal (pi-1, pi+1) that bridges pi lies entirely in P. We say that two ears pi and pj are non-overlapping if the interior of triangle (pi-1, pi, pi+1) does not intersect the interior of triangle (pj-1, pj, pj+1)
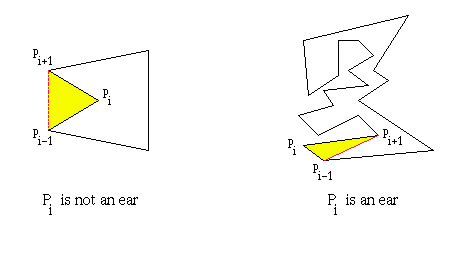
Note: The program code uses 'Polygon Triangulation in C#' of fgshen (http://www.codeproject.com/csharp/cspolygontriangulation.asp) as skeleton triangulation code. For more info about the triangulation and two-ears theorem, please check the page.
3-coloring
Graph 3-coloring is the task of coloring each node of the graph either red, green, or blue with the constraint that the two endpoints of any edge must get different colors.

Using the code
Basically the code is developed with Visual Studio 2005 using C#. The code uses the System.Drawing library for most drawing and computational-geometry.
Here's a class list for the code.

Triangulation - triangulate()*
Handles the two-ears theorem triangulation algorithm.
public void triangulate() // triangulate the bigger polygon-shape
{
mPolygon poly = new mPolygon(updated_vertices);
// create a polygon from the current vertices
Boolean finished = false; // triangulation-finished?
if (updated_vertices.Length == 3)
// if there's only 3 points, no need to run algorithm
finished = true;
Point p = new Point();
while (finished == false)
// loop while triangulation not finished yet
{
int i = 0;
Boolean not_found = true;
// did we found an ear? no, not yet
while (not_found && (i < updated_vertices.Length))
// while we did not found any ear and
// not yet processed all vertices
{
p = updated_vertices[i]; // get current point
if (is_ear(p))
// check if we can get an ear from that vertice
not_found = false; // good we found one
else
i++; // continue to search
}
update_vertices(p);
// remove the vertice we found the ear
// from the updated_vertices list
poly = new mPolygon(updated_vertices);
// reupdate the polygon from the rest of vertices
if (updated_vertices.Length == 3)
// if there's only 3 vertice left
finished = true;
// this means we finished the triangulation
}
// when the CS:IP reaches here, this means triangulation finished
polygons = new Point[ears.Count + 1][];
// init polygons structure to ears.count +
// 1(for last 3 points left)
for (int i = 0; i < ears.Count; i++)
{
Point[] points = (Point[])ears[i];
// move ears to final triangulated polygons list
polygons[i] = new Point[3];
polygons[i][0] = points[0];
polygons[i][1] = points[1];
polygons[i][2] = points[2];
}
// we have 3 left vertices on updated_vertices list,
// - the last triangulated polygon -
polygons[ears.Count] = new Point[updated_vertices.Length];
// add it to triangulated polygons list also
for (int i = 0; i < updated_vertices.Length; i++)
{
polygons[ears.Count][i] = updated_vertices[i];
}
}
Triangulation - is_ear()*
Check if given point is in a valid ear.
private Boolean is_ear(Point p) // checks if given vertice is in a ear
{
mPolygon m = new mPolygon(updated_vertices);
// init. a polygon from the current vertices
if (m.is_vertex(p) == true) // if given point is a vertex
{
if (m.vertex_type(p) == VertexType.ConvexPoint)
// and it's a convex point
{
Point curr_point = p;
Point prev_point = m.get_prev_point(p);
// find previous adjacent point
Point next_point = m.get_next_point(p);
// find next adjacent point
for (int i = updated_vertices.GetLowerBound(0);
i < updated_vertices.GetUpperBound(0); i++)
// loop through all other vertices
{
Point pt = updated_vertices[i];
if (!(is_points_equal(pt, curr_point) ||
is_points_equal(pt, prev_point) ||
is_points_equal(pt, next_point)))
{ // if pt is not equal to checked vertice or
// its's next and prev adjacent vertices
if (is_point_in_triangle(new Point[]
{ prev_point, curr_point, next_point }, pt))
// check pt lies in triangle
return false;
// if another vertice lies in this
// triangle, then this is not an ear
}
}
}
else // concave
return false;
// we cannot make ears from concave points
return true; // if CS:IP reaches here, this means
// vertice passed the test and is an ear
}
return false; // if the given vertex is not an vertex,
// it's not related to an ear also!
}
3-Coloring - traverse()
Start point for 3-coloring algorithm. Colors the last processed polygon and calls the deep-first coloring algorithm
public void traverse() // travers the triangulated polygons list for
// assigning 3-colors
{
int last_poly = polygons.Length - 1; // find last polygon on list
lb.Items.Add("[p" + last_poly + "] Last Polygon: \t" +
polygons[last_poly][0] + polygons[last_poly][1] +
polygons[last_poly][2]); // debug message
// directly assign last polygons vertex's colors
vertex_colors[get_index(polygons[last_poly][0])] = vertex_color.Red;
vertex_colors[get_index(polygons[last_poly][1])] = vertex_color.Blue;
vertex_colors[get_index(polygons[last_poly][2])] = vertex_color.Green;
colorize(0); // start deep-first 3-color algorithm
}
3-Coloring - colorize()
Deep-first algorithm to assign colors for vertexes.
public void colorize(int i) // algorithm for colorizing points
{
int next = i + 1;
if (next < input_vertices.Length) // use deep-first strategy
{
colorize(next);
}
find_polygons(input_vertices[i]); // find given points related polygons
}
3-Coloring - find_polygons()
Find polygons related for a given point. Used in 3-coloring algorithm for finding a given points related polygons and if there's non-color assigned vertex in that found polygon, the code assigns it a color.
public void find_polygons(Point p) // find given points related polygons
{
int v0_index, v1_index, v2_index;
for (int i = polygons.Length - 1; i > -1; i--)
// loop through all polygons
{
if ((p == polygons[i][0]) || (p == polygons[i][1]) ||
(p == polygons[i][2]))
// if given point is one of the vertexes of current polygon
{
for (int j = 0; j < 3; j++)
// check polygons all 3-vertexes colors
{ // vertexes are rounded and each one is
// checked with two other
v0_index = get_index(polygons[i][j]); // vertex1
v1_index = get_index(polygons[i][(j + 1) % 3]);
// vertex2
v2_index = get_index(polygons[i][(j + 2) % 3]);
// vertex3
if (vertex_colors[v0_index] == vertex_color.Empty)
// if selected vertex's color is not set yet
{
vertex_colors[v0_index] =
find_color(vertex_colors[v1_index],
vertex_colors[v2_index]);
// try to set a color to it using
// other two vertexes colors
lb.Items.Add("[s" + v0_index + "]
Assigned color: \t" + str_color
(vertex_colors[v0_index]) + " {" +
str_color(vertex_colors[v1_index]) +
" ," + str_color(vertex_colors[v2_index]) +
"} " + polygons[i][j]); // debug message
}
}
}
}
}
Running the program
Drawing a polygon
Using the left mouse button, mark the vertices of the polygon.
Use the right mouse button to let program finalize the polygon.
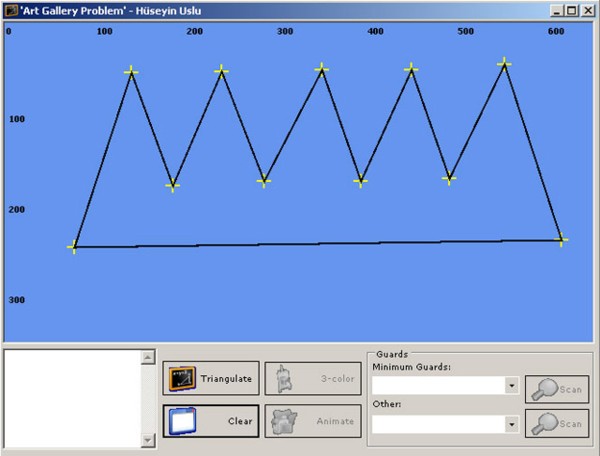
Triangulate
Use the Triangulate button to let program run triangulation algorithm.

3-Color
Use the 3-Color button to let program 3-color the vertices.

Animation
The program can animate the 3-coloring algorithm both using the animate button or by clicking a step in listbox.

Guard-Scanning
The program can scan selected guards view area by the scan buttons.

History
- 04.05.2007 - Initial post

References
* Triangulation code mostly based on http://www.codeproject.com/csharp/cspolygontriangulation.asp
