A short discussion on mapping 3D objects onto a 2D display.
This article describes, in simple terms, how to translate three dimensional co-ordinates into the two dimensional co-ordinates to be displayed on a screen.
It is intended to be an introduction to the basics of rendering 3D images and does not cover topics like rotation or movement.
A few basic definitions and assumptions
The co-ordinate system that we will be working in is the standard Cartesian co-ordinate system as depicted in figure 1.
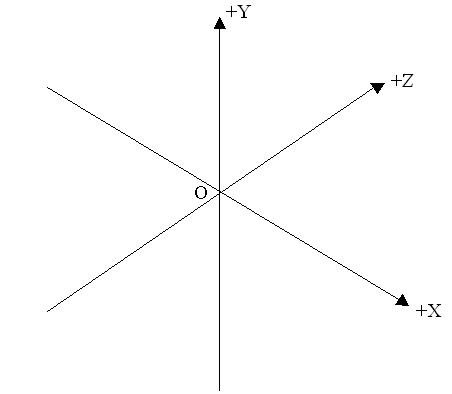
where: o is the origin
+x is
to the right (-x is to the left)
+y is up
(-y is down)
+z is
forwards (-z is the opposite direction)
A point within this 3D space can have it's location represented as P(x, y, z) representing it's position relative to our origin defined
above. A polygon will simply be a collection of such points joined by lines.
Next, we also need to define where we are looking from (the viewpoint). This will be
the position of the camera E. In order to simplify the explanation a
little, the camera will be placed at the origin
(0, 0, 0). Later in
this article, we will move the camera away from the origin. Another
simplification can be made by assuming that the camera is always looking along
the Z axis towards +Z. The maths is more complicated if this is not so, and I won't discuss
that here.
Finally, we need somewhere to project the image onto, screen S. This will always be in a plane that is at right angles to the
direction we are viewing and at a distance of Sz from the origin. This screen
can be assumed to extend as far as required. Figure 2 show the current scenario:

Seeing the point
If we view the scene from along the X axis, we get a 2D cross section of the YZ plane (looking towards the origin from the positive
side). Now we draw an imaginary line between the camera and the point we want to show on the screen, we can see that line will
intersect the screen at a point S. Figure 3 illustrates this.

We already know the z co-ordinate for our screen point (Sz, same as the screen) we need to work out it's y value.
Basic Trigonometry can give us the answer here. Using the rules for similar triangles, we can see that the ratio of
Sz over Pz is the same as the ratio of Sy over Py; Written as an equation, we have:-
Sz = Sy<br>
Pz Py
and re-arranging the formula gives the following equation for Sy;
Sy = Py Sz<br>
Pz
A similar process will result in a similar equation for the X co-ordinate.
Sx = Px Sz<br>
Pz
You can see that if we have another point P2, as shown in figure 4, which has the same X and Y values but a different Z value,
you can see that it intersects the screen at a different point. This mimics the perspective effect we notice in real life.
Objects further away appear to be smaller than those that are nearer.

Moving the camera is away from the origin?
The formula given above are valid only when the co-ordinates are presented relative to the the origin (ie (0, 0, 0).
If the camera is not at the origin, we need to adjust the formulae to account for this. Figure 5 shows the camera moved along the Y axis
and the Z axis.

If we go back to the first equations and adjust them for the offset, we have:
(Sz-Ez) = (Sy-Ey)<br>
(Pz-Ez) (Py-Ey)
and re-arranging the formula gives us
(Sy-Ey) = (Py-Ey)*(Sz-Ez)<br>
(Pz-Ez)
so, we end up with
Sy = (Py-Ey)*( Sz-Ez) + Ey<br>
( Pz-Ez)
Similarly doing a similar transformation for Sx,
Sx = (Px-Ex)*( Sz-Ez) + Ex<br>
( Pz-Ez)
About the program
With this being Code Project, I suppose it's useful to supply some code. The demonstration
program is something I wrote to show the effect of changing some of the parameters that affect the rendering of the image.
I have used Chris Maunder's 3D
classes, but most of the functionality in those classes is not used.
Using the program
When you run the program, you are presented with three 'wire frame' houses which are in fact all the same size, but placed at different
Z co-ordinates. You can use the toolbar buttons or the keyboard to move the camera around.
The following keys do things in the program:
K/L: Move the position of the screen along the 'Z' axis
A/D: Move the position of the camera along the 'X' axis
W/X: Move the position of the camera along the 'Y' axis
R/T: Move the position of the camera along the 'Z' axis
Pressing the toolbar buttons will move the camera in the direction indicated by the button icon (if you can decode my artistic efforts)
This member has not yet provided a Biography. Assume it's interesting and varied, and probably something to do with programming.
 General
General  News
News  Suggestion
Suggestion  Question
Question  Bug
Bug  Answer
Answer  Joke
Joke  Praise
Praise  Rant
Rant  Admin
Admin 









