Solve Linear and Polynomial Equations
4.91/5 (16 votes)
This is used to Solve Linear or Polynomial equations.
Introduction
Linear and polynomial equations are used in many different applications. So solving these equations is useful for many people. This application has the method to solve the linear and polynomial equations. The user can select Polynomial or Linear equation and then give the relevant parameters. There is a GUI form to input the parameters for easy understanding of the user.
Background
Linear Equations
The equation in the below format is called a linear equation:
51x+4y+38z = 35
In the above equation, x, y and z are unknowns. If you want to solve 3 unknowns, you need 3 equations with those unknowns.
Polynomial Equations
The equation in the below format is called polynomial equation:
4x^3+7x^2-12=0
Polynomial equation has only one unknown variable. In the above equation, x is the unknown variable. Maximum power of the unknown variable is called the order of the equation. Order of the above equation is 3. Maximum number of solution for a polynomial equation is the order of that equation.
Solve Equation
The number of unknowns should be equal to the number of the equation to get a solution for linear equations. Matrix row operations are used to solve the Linear equation. Newton-Raphson method is used to solve polynomial equation.
The program has three GUI forms to get inputs from the user. The first form is to get the type of the equation and the number of the parameters for the equation. In other words, the number of unknowns or order of the equation.
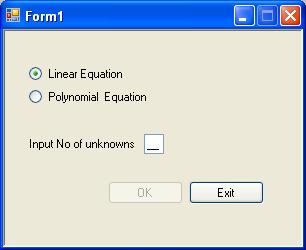
Solve Linear Equation
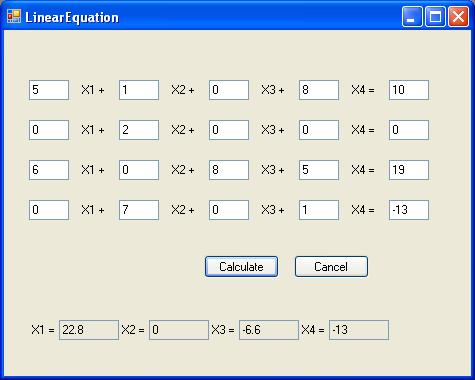
The above form is use to get inputs for solving linear equations. Fill the tables with the relevant values. Unknowns are indicated as X1, X2, ..., etc. Then click the "Calculate" button.
Solve Polynomial Equation
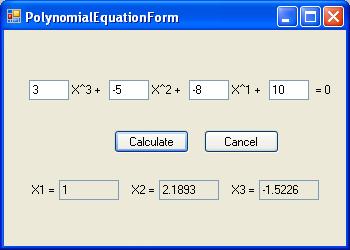
The above form is used to get the input from the user. The text boxes below give the Output values after click "Calculate" button.
Using the Code
Solve Linear Equation
Assume you need to solve the below 3 equations:
4x+23y-6z = 3-7x+3y+12z = 255+10y-7z = 30
It can be written in matrix production as below:
[4 23 -6] [x] .. [ 3]
[-7 3 12] [y] = [25]
[5 10 -7] [z] .. [30]
3 matrices are there:
- coefficient matrix(3,3)
- unknown variable matrix(3,1)
- answer matrix(3,1)
Assume that the number of unknowns are 'n'. Then consider the first matrix(n,n) and third matrix(n,1), combine both matrices and create a 2D array (n,n+1).
Example (for the above equations):
[4 23 -6 | 3]
[-7 3 12 |25]
[5 10 -7 |30]
Then make a coefficient matrix as unit matrix by row operations. The matrix multiplication will not change by the row operation. So the answer matrix becomes the solution of the unknowns.
for (int i = 0; i < nVar; i++)
{
//If the element is zero, make it non zero by row operation
if (equationMatrix[i, i] == 0)
{
int j;
for (j = i+1; j < nVar; j++)
{
if (equationMatrix[j, i] != 0)
{
for (int k = i; k < nVar + 1; k++)
equationMatrix[i, k] += equationMatrix[j, k];
break;
}
}
//If all value for this variable is zero, there should a duplicated equation
if (j == nVar)
throw new Exception("Same equation repeated. Can't solve it");
}
//make the diagonal element as 1
for (int k = nVar; k >= i; k--)
equationMatrix[i, k] /= equationMatrix[i, i];
//use row operation to make upper matrix
for (int j = i+1; j < nVar; j++)
{
for (int k = nVar; k >= i; k--)
equationMatrix[j, k] -= equationMatrix[i, k]*equationMatrix[j,i];
}
}
//It is to make diagonal matrix
for (int i = nVar-1; i > 0; i--)
{
for(int j=i-1; j>=0; j--)
{
equationMatrix[j, nVar] -= equationMatrix[j, i] * equationMatrix[i, nVar];
equationMatrix[j, i] = 0;
}
}
double []ans = new double[nVar];
for(int j=0; j < nVar; j++)
ans[j] = equationMatrix[j,nVar];
Solve Polynomial equation
It uses Newton-Raphson method. It is an approximation method. So it needs more iterations to get more accurate values. This program has an accuracy around 0.0001. The number of iterations changes according to the accuracy of the answer.
while (Math.Abs(x - x0) > 0.0001)
{
if (itr++ > maxIteration)
{
return NoSolution;
}
x0 = x;
func = 0; dFunc = 0;
for (int i = 0; i < coefficient.Count; i++)
{
func += coefficient[i] * Math.Pow(x, coefficient.Count-1 - i);
}
for (int i = 0; i < dCoeff.Count; i++)
dFunc += dCoeff[i] * Math.Pow(x, dCoeff.Count-1 - i);
if (dFunc != 0)
x = x - func / dFunc;
else if (func < 0.0001)
return x;
else
x += 1;
}
Note
The methods "List<double> SolvePolynomialEquation(List<double> coeffient)" and "double[] SolveLinearEquation(double[,] equationMatrix)" had the capability to solve the equations which have the order of more than 10. I restricted order of the equations to 10 in this program.
Points of Interest
There is an initial value and then approximation method used to get the solution for polynomial equation. If you know the approximation value for the equation, then give that value to reduce the iterations.
History
- 2nd November, 2011: Initial version
