Number crunching: Why you should never, ever, EVER use linked-list in your code again
4.86/5 (73 votes)
Most programming resources are wrong when comparing linked-list to vector. Here you can read and understand how they are wrong and why linked-list is (mostly) to be avoided.

Mea Culpa - Please read before continuing
Let us look at the title again. It contains a very important prefix. The title says:
Number crunching: Why you should never, ever, EVER use linked-list in your code again.
The number crunching prefix is key to this whole article. If the "Number crunching:" part of the title is ignored it might be understood as a general advice to always stay away from linked-list, that is not the purpose of this article.
The point of the article is to explain why linked-list is so badly suited for number crunching tasks. What number crunching is will soon be explained. Even so there are of course always exceptions to the rule and so the title cannot be 100 percent true.
The title above is a hyperbole. It strongly emphasizes a purpose but being deliberately over the top. Since I do have mixed feelings about it, and obviously so do some readers then a possible title change could be:
Why you should never, ever, EVER use linked-list for number crunching
However I decided to keep it since it could be more confusing to change it. A few readers have also commented that they think the title is just right. So let's just leave it with that.
Now, why on earth did I decide in the first place for such a CodeProject unusual act as to put a hyperbole title on the article? Honestly, because the message needed to get out. My impression is that the performance impact of using a linked-list for number crunching is not commonly known and that is why I decided to write this article.
I hope with this Mea Culpa you can see beyond any initial confusion which is all my fault and see to the core issue: the cons of linked-list for a set of number crunching problems.
Table of Contents
- Mea Culpa - Please read before continuing
- Introduction
- In Real Life
- Table of Contents
- Disclaimer
- Scope
- On-line resources
- Important Stuff comes now
- Locality of Reference I
- The Code
- Locality of Reference II
- Devils Advocate
- Devil's Advocate I - Cost of copying
- Devil's Advocate II : Linear, sorted insert with smart linked-list
- Devil's Advocate III : Fragmented memory makes vector a big no-no
- Devil's Advocate IV : Algorithms with merge or sort
- Devil's Advocate V : Insert at first position
- What to Do Now?
JavaandC#- Conclusion
- References
- History
Introduction
This article will explain why the linked-list is a less then ideal choice for dealing with number crunching.
Number crunching is the term used here for describing the crunching, sorting, inserting, removing and simply juggling of raw numbers or POD data. This article is about why linked-list is not well suited for these tasks and should in fact be avoided. It is written with an attitude but backed up with facts and proofs. You are welcome, even encouraged, to verify these claims and all code and proofs are either accessible online or are available to download.
The intention is to clearly show some obvious examples to prove a point. The article is not written to cover every special case and exception to its recommendation.
These obvious examples are for some readers edge cases, for other readers it is common programming tasks. Some readers think the point of the article is common sense, others that it is a joke and are shocked when they realize that it is in fact reality. I especially recommend the latter readers to not easily dismiss this article but in fact take time to study it. You might just get a new insight.
In Real Life
Number crunching tasks are sometimes similar to my examples below, sometimes not. They can be found in a variety of areas such as avionics technology, heart surgery equipment, surveillance technology and [...] well you name it. What to remember as you continue is that number crunching as used in this article is referring to numbers and POD data that is stored, retrieved, removed and sorted. Nothing weird, and very common and are always types that are cheap to copy
A few times in my professional career I have encountered performance issues where some time critical areas got bad performance just because of number crunching by linked-list. I have witnessed these linked-list related performance issues in a range of areas from real-time, embedded, small memory constrained PowerPC systems to x86 PC applications.
These times it came as a complete surprise to those involved. It was a surprise because to them it was proven by mathematical complexity models that it was a very efficient data structure for this or that use. That it was slow was considered bad, but OK, because other data structures would be slower according to the same mathematical line of reasoning.
Unfortunately for a given problem set these mathematical models are likely to lead you astray. Following blindly the Big-O complexity of the data structures and algorithms might lead you to a conclusion that is completely and utterly false.
Big-O notations tells nothing about how one (data structure with algorithm) fare against another. Big-O will only tell you how performance will degrade as n increases. So comparing one a data structure that is RAM intensive to another data structure that is cache friendly from an abstract Big-O point-of-view is just pointless. This is nothing new, but since the books and online resources rarely, or ever, mention this not many know about it, or at least tend to forget.
Disclaimer
Just in case my Mea Culpa and Introduction did not cover it. Let me be clear: This article is not disqualifying the linked-list for other types of usages, such as when it contains types that have pointers to other types, large and expensive-to-copy types (and yes, POD can also be too large).
This article is not about specific usage patterns where linked-list makes extra sense - because there sure are several of those. Take a peek later in the comments section and you can find several more, or less, good examples of such cases. This article is an opinionated article but backed up with hard facts. It does not discredit linked-list overall except in one specific area: number crunching.
Other types of containers are used to compare with the linked-list. The purpose is not to hype these containers but to show the areas where linked-list is lacking. It even goes as far as using these containers in clearly suboptimal ways which still by far outperforms the linked-list.
The code examples and container names in this article are from C++. std::vector would in Java be called ArrayList and the Linked-list in C++ is called std::list, which in Java it would be called LinkedList
OK, enough with the disclaimer, lets get going.
Scope
What data structure should you use? What data structure should you avoid?
Imagine that you have to use a data structure. It is nothing fancy, only a storage for raw numbers, or POD data carriers that you will use now and then and some later on.
These items will be inserted, then removed intermittently. They will have some internal order, or significance, to them and be arranged accordingly. Sometimes insertions and removal will be at the beginning or the end but most of the times you will have to find the location and then do an insertion or removal somewhere in between. An absolute requirement is that the insertion and removal of an element is efficient, hopefully even O(1).
Now, what data structure should you use?
On-line resources
At a time like this it is good advice to double check with books and/or on-line resources to verify that your initial hunch was correct. In this situation maybe you recollect that vectors are generally fast for accessing an item but can be slow in modifying operators since items not at the end that are inserted/removed will cause part of the contents in the array to be shifted. Of course you also know that an insertion when the vector is full will trigger a re-size. A new array storage will be created and all the items in the vector will be copied or moved to the new storage. This seems intuitively slow.
A linked list on the other hand might have slow O(n) access to the item but the insertion/removal is basically just switching of pointers so this O(1) operations are very much appealing. I double check with a few different online resources and make my decision. Linked-list it is…
BEEEEEEEEP. ERROR. A RED GNOME JUMPS DOWN IN FRONT OF ME AND FLAGS ME DOWN. HE TELLS ME IN NO UNCERTAIN WAYS THAT I AM WRONG. DEAD WRONG.
www.cplusplus.com/reference/stl/list Regarding std::list[...] Compared to other base standard sequence containers (vector and deque), lists perform generally better in inserting, extracting and moving elements in any position within the container, and therefore also in algorithms that make intensive use of these, like sorting algorithms.
www.cplusplus.com/reference/stl/vector Regarding std::vector[...] vectors are generally the most efficient in time for accessing elements and to add or remove elements from the end of the sequence. [...] For operations that involve inserting or removing elements at positions other than the end, they perform worse than deques and lists.
http://en.wikipedia.org/wiki/Sequence_container_(C%2B%2B)#List Vectors are inefficient at removing or inserting elements other than at the end. Such operations have O(n) (see Big-O notation) complexity compared with O(1) for linked-lists. This is offset by the speed of access — access to a random element in a vector is of complexity O(1) compared with O(n) for general linked-lists and O(log n) for link-trees.
In this example most insertions/removals will definitely not be at the end, this
is already established. So that should mean that the linked-list
would be more effective than the vector, right? I decide to double check with
Wikipedia,
Wiki.Answers and
Wikibooks on Algorithms. They all seem to agree and I cannot understand what
the RED GNOME is complaining about.
I take a break to watch
Bjarne Stroustrup’s Going Native 2012 keynote. At time 01:44 in the video-cast
and slide 43, something interesting happens. I recognize what the RED GNOME
has tried to to tell me. It all falls into place. Of course. I should have known.
Duh. Locality of Reference.
Important Stuff comes now
It does not matter that the linked-list is faster than vector for inserting/removing an element. In the slightly larger scope that is completely irrelevant. Before the element can be inserted/removed the right location must be found. And finding that location is extremely slow compared to a vector. In fact, if both linear search is done for vector and for linked-list, then the linear search for vector completely, utterly and with no-contest beats the list.
- The extra shuffling, copying overhead on the vector is time-wise cheap. It is dirt cheap and can be completely ignored if compared to the huge overhead for traversing a linked-list.
Why? you may ask? Why is the linear search so extremely efficient for vector compared to the supposedly oh-so-slow linked-list linear search? Is not O(n) for linked-list comparable to O(n) for vector?
In a perfect world perhaps, but in reality it is NOT! It is here that Wiki.Answers and the other online resources are wrong! as the advice from them seem to suggest to use the linked-list whenever non-end insertion/removals are common. This is bad advice as they completely seem to disregard the impact of locality of reference.
Locality of Reference I
The linked-list have items in disjoint areas of memory. To traverse the list the cache lines cannot be utilized effectively. One could say that the linked-list is cache line hostile, or that the linked-list maximizes cache line misses. The disjoint memory will make traversing of the linked-list slow because RAM fetching will be used extensively.
A vector on the other hand is all about having data in adjacent memory. An insertion or removal of an item might mean that data must be shuffled, but this is cheap for the vector. Dirt cheap (yes I like that term). The vector, with its adjacent memory layout maximizes cache utilization and minimizes cache line misses. This makes the whole difference, and that difference is huge as I will show you soon.
Let us test this by doing insertions of random values. We will keep the data structure sorted and to get to the right position we will use linear search for both vector and the linked-list. Of course this is silly way to use the vector but I want to show how effective the adjacent memory vector is compared to the disjoint memory linked-list.
The Code
/* NumbersInVector &randoms is pre created random values that are stored in a
std::vector. This way the same random values can be used for testing and comparing the
vector to the linked-list.
Example:
0, 1, 8, 4, 1 will get sorted to:
0, 1, 1, 4, 8 */
template <typename Container>
void linearInsertion(const NumbersInVector &randoms, Container &container)
{
std::for_each(randoms.begin(), randoms.end(),
[&](const Number &n)
{
auto itr = container.begin();
for (; itr!= container.end(); ++itr)
{
if ((*itr) >= n) { break; }
}
container.insert(itr, n); // sorted insert
});
}
/* Measure time in milliseconds for linear insert in a std container */
template <typename Container>
TimeValue linearInsertPerformance(const NumbersInVector &randoms, Container &container)
{
g2::StopWatch watch;
linearInsertion(std::cref(randoms), container);
auto time = watch.elapsedMs().count();
return time;
}
The time tracking (StopWatch that I wrote about here) is easy with C++11... Now all that is needed is the creation of the random values and keeping track of the measured time for a few sets of random numbers. We measure this from short sets of 10 numbers all the way up to 500,000. This will give a nice perspective
void listVsVectorLinearPerformance(size_t nbr_of_randoms)
{
std::uniform_int_distribution distribution(0, nbr_of_randoms);
std::mt19937 engine((unsigned int)time(0)); // Mersenne twister MT19937
auto generator = std::bind(distribution, engine);
NumbersInVector values(nbr_of_randoms);
// Generate n random values and store them
std::for_each(values.begin(), values.end(), [&](Number &n)
{ n = generator();});
NumbersInList list;
TimeValue list_time = linearInsertPerformance(values, list);
NumbersInVector vector;
TimeValue vector_time = linearInsertPerformance(values, vector);
std::cout << list_time << ", " << vector_time << std::endl;
}
Calling this for values going all the way up to 500,000 gives us enough values to plot them in a graph and which shows exactly what Bjarne Stroustrup told us at the Going Native 2012. For removal of items we get a similar curve but that is not as time intensive. I have google doc collected some timing results that I made on IdeOne.com and on a x64 Windows7 and Ubuntu Linux laptop for you to see.

Can you see the red fuzz at the bottom? The graph is not displayed incorrectly. That red fuzz is the time measurements for vector. 500,000 sorted insertions in a linked-list took some 1 hour and 47 minutes. The same number of elements for the vector takes 1 minute and 18 seconds.
You can test this yourself. The code is attached with this article. For a quick test you can try out the smaller (max 15 seconds) test of up to 40.000 elements at the pastebin and online compiler IdeOne: http://ideone.com/62Emz
Locality of Reference II
The processor and cache architecture has a lot of influence on the result obviously. On a Linux OS the cache level information can be retrieved by
grep . /sys/devices/system/cpu/cpu*/cache/index*/*
On my x64 quad-core laptop that gives each core-pair 2x L1 cache a 32 KBytes and with a cache line size of 64 bytes. 2x L2 cache a 256 KBytes. All cores share a 3 MBytes L3 cache.

Conceptual drawing of quad core Intel i5
I thought it would be interesting to compare my quad-core against a simpler and older computer. Using the CPU-Z freeware software I got from my old dual-core Windows7 PC that it has 2xL1 caches a 32KBytes and 1xL2 cache a 2048 KBytes. Testing both with a smaller sets of values shows the cache significance clearly (disregarding different bus bandwidth and CPU Speed )

x86 old dual-core PC

x64 quad-core Intel i5
Devils Advocate
Of course there are always exceptions, special cases, and objections to either using vector or the advice of not using linked-list. If we can ignore the obvious non-related cases and focus on just the POD or number crunching then there are still some valid concerns that should be addressed.
Devil's Advocate I - Cost of copying
For vector the traditionally perceived overhead for copying, shuffling and resizing (with memory allocations and copying) is sufficient reasons for some (ref: [2] to [7]) for choosing the linked-list over the vector.
Above was shown how the perceived inefficiency of the vector was in fact dirt cheap compared to the cost of traversing a linked-list. The linked-list item insertion is cheap but to get to the insertion place a very expansive traversal in disjoint memory must be done.
The examples above are somewhat extreme. The integer examples brings out another bad quality of linked-list. The linked-list need 3 * size of integer to represent one item when the vector only need 1. So for small data types it makes even less sense to use a linked-list.
However, what would happen if the cost of copying was not so cheap? If the cost for modifying the vector would increase?
For larger types you might see the same behavior as shown above but obviously the times would differ. As the types grow in size and becoming more expensive then finally the linked-list would outperform the vector which has to shuffle and copy a lot of objects. Using the C++ move operator would perhaps change this. I have not tested with move operator so that is up to you to try out for yourself.
As PODs grow larger in size, the copying cost will also grow. The overhead in copying and shuffling will take its toll. The cache architecture and the cache's line size will also make an impact. If the POD size is larger than the cache-line size then the cache usage will be suboptimal compared to when used for smaller POD size.
At some POD size this extra overhead will even be more time consuming then the linked-list slow traversal. At this point choosing to use a vector is a worse choice then choosing the linked-list, even for the scenario used earlier in this article.
This is shown in the three graphs below. The tests were done for 200, 4000 and 10.000 elements. Each graph represents a fixed number of elements, where the byte size of the PODs is increasing.
Observe the intersection between the linked-list and the vector performance. It is at the intersection that the performance goes from being in favor of vector to being in favor of linked-list for that number of elements

From the graphs it is obvious that for the same number of elements the POD size has virtually no impact on the linked-list performance. For vector the POD size is of massive importance. The cost of copying increase proportionally with the size.

Efficiency when using the linked-list is limited by the cost of RAM access and thus almost POD size ignorant. However as the number of items increase the total cost for RAM access will be more expensive and substantially larger PODs (bytes) are needed before linked-list will outperform the vector.

The data is collected in a google document and also in the download area in excel format. A quick look using ideone.com can be done at ideone.com/W9vpT and also available with the downloads.
Devil's Advocate II : Linear, sorted insert with smart linked-list
A common objection to the linear, sorted insert comparison shown above is that since the linked-list linear is known to be slow the iterator to the last inserted location should be kept. That way on average the linear search could benefit from O(n/2) instead of O(n).
When testing this it showed what huge impact the cache architecture has on the performance on adjacent memory structures. The first test run was made at ideon.com/XprUU. The ideone online compiler has unknown cache architecture and since it is serving multiple runs simultaneously it is likely that the caches utilization is unpredictible and RAM usage is heavy.
With this likely cache under utilization the smart linked-list was clearly the winner. At least up to a certain number of elements. It took up to 6000 elements before the vector had caught up to the smart linked-list. This was a huge surprise to me! but it made sense when I tested it with a known cache architecture.

The same test was run on a known cache architecture, my x64 laptop, with L1, L2 and L3 cache. It immediately showed the benefits of cache utilization for adjacent memory structures. The smart linked-list and the vector kept even pace up to about 100 elements, at 500 elements the difference was around 20 percent and steadily increasing.

If you take a peek at its data sheet you can see the performance data both when running at ideone.com/XprUU and on the x64 laptop.
On other computers with different cache architectures and when using other languages (Java, C#, etc) this will give different results..
Devil's Advocate III : Fragmented memory makes vector a big no-no
For fragmented memory, or systems where the memory can be suspected to be fragmented, or for huge
vectors, then it might be beneficial to use list-of-vectors instead. There are a few different types to choose from: unrolled linked-lists [12] or the std::deque are two.
I have not tested the fragmented memory scenario as I simply could not come up with a way to force the memory to be easily fragmented. On 32-bit dual-core PC and 64-bit quad-core PC I never once encountered allocation exception, even for multiples of the 500.000 items comparison testing.
Devil's Advocate IV : Algorithms with merge or sort
Yes, what about it? The online resources pointed out earlier are stating that
merge or sort of the containers is where the linked-list will outperform the vector. I am sorry to say but this is not the case for a computer with a modern cache architecture. At least not in the area of number crunching, and is it not there that sort
are most commonly used?
Once again these resources are giving you bad advice.
From a mathematical perspective YES it does makes sense when calculating big-O complexity. The problem is that the mathematical models (at least the ones I have seen) are flawed. At least flawed in that aspect that making a decision for what to use from the big-O complexity value is just not good enough.
Computer cache, RAM and memory architecture are completely disregarded and only the mathematical, SIMPLE, complexity is regarded.
To show this some simple sort testing is laid out below.
void listVsVectorSort(size_t nbr_of_randoms)
{
std::uniform_int_distribution<int> distribution(0, nbr_of_randoms);
std::mt19937 engine((unsigned int)time(0)); // Mersenne twister MT19937
auto generator = std::bind(distribution, engine);
NumbersInVector vector(nbr_of_randoms);
NumbersInList list;
std::for_each(vector.begin(), vector.end(), [&](Number& n)
{ n = generator(); list.push_back(n); } );
TimeValue list_time;
{ // list measure sort
g2::StopWatch watch;
list.sort();
list_time = watch.elapsedUs().count();
}
TimeValue vector_time;
{ // vector measure sort
g2::StopWatch watch;
std::sort(vector.begin(), vector.end());
vector_time = watch.elapsedUs().count();
}
std::cout << nbr_of_randoms << "\t\t, " << list_time << "\t\t, " << vector_time << std::endl;
}
The sort testing I made is available on the
google spreadsheet on tab “sort comparison“. I used std::sort (vector) vs std::list::sort.
Sure, it is two different algorithms who likely use two different algorithms so this test might be a leap of faith. Either way it can be interesting since both algorithms are at their best and this is where the linked-list supposedly should be the winner. No big surprise that it was not.
The std::sort (vector) beats the std::list::sort hands-down. The complete code is attached and available here http://ideone.com/tLUeK.
The graph below show the sort performance from 10 up to 1.000 elements. The cost is always higher for the linked-list. Both show a proportional cost increase as the number of elements increase but the linked-list has a steeper incline. The linked-list sorting will compared to the vector be obviously more expensive per item as the elements increase.
Testing this on a modern x64 computer with better CPU-cache architecture would increase the difference between std::list and vector even more.

As the number of elements continue to grow this initial performance perspective does not change. The graph below shows from 10 to 100.000 elements but has virtually the same proportional properties as when compared 10 to 1.000.

The corresponding sort test but for merge was not tested. However, for merge of two sorted structures, that after the merge should still be sorted, then that involves traversal again and once again the linked-list is no good.
Devil's Advocate V : Insert at first position
A reader wrote in the comments below:
“[If] Your insertion is always done [at] the index 0 or somwhere in the middle. No matter how large list grows the operation perfomed in constant time O(1). With vectors it is O(log(n)). The larger the array the slower the insertion.”Another reader wrote in my blog :
“[A] very common example when adding elements to the beginning a list. Using a LinkedList this would be a fairly simple operation (just swapping some pointers) while the ArrayList [Java version of dynamic array] would struggle to make such insertion (moving the entire array)”
Copy and pasting from my own article comment answer to the first reader:
“What you wrote above is completely accurate. You are not the first to mention this and while it is so right it is also so wrong. Let me explain.
The scenario you outlined is very believable. In fact putting one piece of data in front of an older piece of data and so forth is perhaps the most common task for data collecting?
In this scenario it makes sense to do insert at “index 0” for the linked-list. This does not makes sense for the vector.
The default insertion on vector should be done by
push_back. Insertion in the direction of growth. An obvious choice to avoid shifting the whole previous section. This is made abundantly clear in C++ where thestd::vector[^] havepush_back, andinsertbut lacks completely the function.push_frontSo, let us not be silly [naive] here, right? Doing
push_backon the vector instead and comparing that to insert at index 0 on the linked-list that is probably the valid options a programmer would choose from. Don’t you agree?
push_backon the vector does not need to shuffle everything for every new element. The overhead when the vector is full and need to be re-sized still applies.“
A code and performance comparison between these three insertions can be seen at http://ideone.com/DDEJF. It compares between the common linked-list operation : insert at “index 0” vs std::vector push_back vs a naive std::vector “
push_front
From: http://ideone.com/DDEJF. Times are given in microseconds [us]
elements, list, vector, vector (naive)
10, 3, 6, 1
100, 7, 3, 13
500, 43, 7, 83
1000, 70, 10, 285
2000, 149, 27, 986
10000, 928, 159, 22613
20000, 1578, 284, 97330
40000, 3138, 582, 553636
100000, 7802, 1179, 3555756
Exiting test,. the whole measuring took 4266 milliseconds (4seconds or 0 minutes)

What to Do Now?
Donald Knuth made the following statement regarding optimization:
“We should forget about small efficiencies, say about 97% of the time: premature optimization is the root of all evil” .
Meaning that “Premature Optimization” is when the software developer thinks he is doing performance improvements to the code without knowing for a fact that it is needed or that it will greatly improve performance. The changes made leads to a design that is not as clean as before, incorrect or hard to read. The code is overly complicated or obfuscated. This is clearly an anti-pattern.
On the other hand we have the inverse of the extreme Premature Optimization anti-pattern, this is called Premature Pessimization. Premature pessimization is when the programmer chose techniques that are known to have worse performance than other set of techniques. Usually this is done out of habit or just because.
Example 1: Always copy arguments instead of using const reference.
Example 2: Using the post increment ++ operator instead of pre increment ++. I.e value++ instead of ++value.
The cost for incrementing native types pre- or post-increment is inconsequential,but for class types the performance difference can have an impact. So using value++ always is a bad habit that when used for another set of types actually is degrading performance. For this reason it is always better to just do pre increments. The code is just as clear as post increments and performance will never be worse
Using linked-list in a scenario when it has little performance benefit (say 10 elements only touched rarely) is still worse compared to using the vector. It is a bad habit that you should just stay away from.
Why use a bad performance container when other options are available? Options that are just as clean and easy to work with and have no impact on code clarity.
Stay away from Premature Optimization but be sure to not fall into the trap of Premature Pessimization! You should follow the best (optimal) solution, and, of course, common sense without trying to optimize and obfuscate the code and design. Sub-optimal techniques such as linked-list should be avoided since there are clearly better alternatives out there.
Java and C#
One comment got when this article was published was something in the line of
This might be true for C++ but for Java or C# this is not so important.
Those languages are not chosen for speed but for faster development time [etc, etc].
This might be true but actually since the speed aspect will likely hit Java and C# just as fast and hard as C++ code it might still be important.
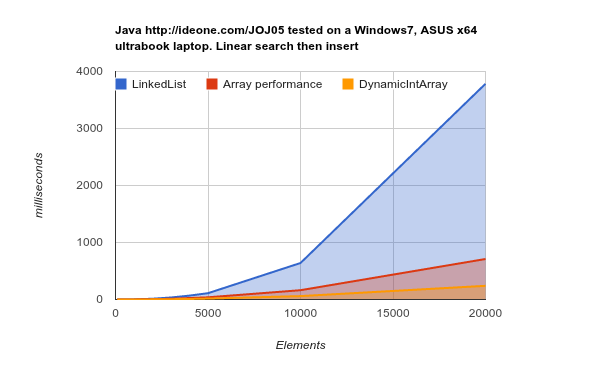
I got help from a friendly reader for a Java try. After some changes proposed by other readers (ref comments) I had a similar linear search, then insert example at http://ideone.com/JOJ05.
In Java the C++ std::list equivalent is called LinkedList. The C++ dynamic array std::vector is in Java called ArrayList.
There is one big difference between these libraries, both the Java LinkedList and ArrayList can only contain objects. This means that the boost of adjacent memory will be somewhat less for an ArrayList containing Integer objects. To access and compare values for the search there is one extra indirection, from reference to value.
To see what difference that made for ArrayList I threw in a DynamicIntArray to get a truly cache friendly structure to compare with. The DynamicIntArray use int, not Integer objects.

For Java the LinkedList showed immediately that it was performing worse than the ArrayList. For the test on ideone.com (http://ideone.com/JOJ05) the LinkedList was performing from a factor of 1.5 to a factor of 3 slower then the best array container.
On my x64 ultrabook the cache architecture is different and the cache friendly structures got a nice boost. The LinkedList was then a factor 1.5 to factor 15 slower then the DynamicIntArray for the same range of elements.
Integer object slow down for ArrayList
On ideone.com the extra indirection overhead of using Integer objects instead of int was roughly a 30% slow down for ArrayList in comparison to the faster DynamicIntArray. On my x64 laptop the ArrayList took roughly twice (200%) as long time to finish as the DynamicIntArray (still faster than at ideone.com)
Much more Java specific testing was presented at my blog but will not fit here. If you would like to read more about it (filtering, sorting, big-O discussion) you can read about it here.
Conclusion
This article is not to discriminate the linked-list for all intents and purposes. It does show however the shortcomings of the linked-list in the area of number crunching.
Traditionally, yes even today, books and online resources almost always completely disregard computer architecture and how this impacts with the concept of locality of reference. These resources calculate algorithm big-O efficiency and makes recommendations that are from just plain wrong as there are huge difference between RAM intense and cache friendly structures. In reality the cache architecture has an enormous impact.
Above I showed some silly usage of C++ std::vector. Instead of using the fast [] operator or some kind of tree structure the scenarious played out equal to not discredit the std::list unnecessarily, in fact some were made to favor the linked-list. It showed that for small, cheap to copy data, raw numbers, or POD an adjacent memory structure is to prefer to a disjoint memory structure. The perceived overhead for new allocations, copying, shuffling that goes with a dynamic array like the Vector is next-to-nothing compared to the very, very slow RAM fetching inolved whenever accessing elements in a linked-list.
When it comes to number crunching then the vector or other adjacent memory structure should be the default and not the linked-list. Of course every new situation needs to be analyzed and data structure and algorithm chosen appropriately. Apply the knowledge you got reading this wisely, only use the linked-list if it will give benefits not easily retrieved from an array-based structure.
Remember that the performance issues with linked-list is usually not the main performance issues for your software. But why using a clearly sub-optimal data structure when the dynamic vector can just as easily be used? Code readability is the same and using linked-list for number crunching is to me an obvious case of
premature pessimization.
When we are in the business of number crunching why not use your understanding of the linked-list disadvantages and stay away from the linked-list for the time being? At least until you are sure you need it. Your code will be better from it and performance will be the same or better, sometimes even much better.
Feedback
I recommend to check out the comments below, maybe leaving one yourself. There are lots of opinions and even some interesting exceptions to my advice and in general very smart comments by equal smart coders. Thanks to them this article got a makeover when I addressed their concerns.
Last, a little plea. Please, before I get flamed to pieces for this obstinate article, why not run some sample code on ideone.com or similar, prove me wrong and educate me. I live to learn =)
Oh, and yes. I know, thank you for pointing it out. There are other containers out there, but this time I focused on linked-list vs vector
References
- Keynote by Bjarne Stroustrup, GoingNative 2012
- cplusplus.com std::list reference
- cplusplus.com std::vector reference
- Wikipedia on sequence containers
- Wiki.Answers: Difference between [Linked-] List and Vector
- WikiBooks: Advantages / Disadvantages [List vs Vector]
- Wikipedia: Linked-List vs Dynamic Array
- Wikipedia: On optimization and Donald Knuth
- CodeProject: Pre-allocated Arrayed List, by Vinod Vijayan
- Blog response by George Aristy Performance comparison: Linked-List vs. Vector [Java]
- Future Chips: Should you ever use Linked-Lists?
- MSDN blogs: Unrolled linked lists
- KjellKod.Wordpress Initial blog version of this article: now mirrored
- KjellKod.Wordpress Java follow up after improvement suggestions from readers
History
- 05/03/2012 Re-published from blog-article http://kjellkod.wordpress.com/2012/02/25/why-you-should-never-ever-ever-use-linked-list-in-your-code-again/
- 06/03/2012 Title update & initial problem scenario clearified... face & fog-lift in process to clear some confusion and better prove the point.
- 19/04/2012 Long overdue makeover. Mea Culpa, Introduction, Disclaimer, Conclusions and general "fog lift". This should remove many earlier misunderstandings... Code examples were added and updated as well.
- 18-21/08/2012 "Devil's Advocate V" + Java section update and minor changes to layout and text. Java was updated due to improvement suggestions and "blog reply" from KjellKod.WordPress (Java Battle Royal)
