Quaternion Mathematics and 3D Library with C# and GDI+
Rotating 3D objects using Quaternion and Drawing 3D objects with GDI+ Graphics

Introduction
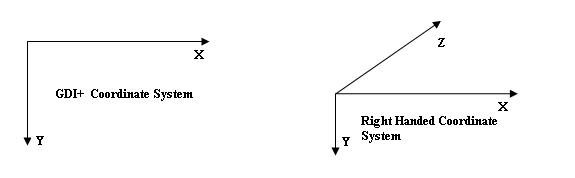
The 3D Library, written using C# and GDI+, allows you to draw pictures in a 3-dimensional space and rotate or/and move 3D objects. The 3D Library includes: Point3d.cs, Vector3d.cs, Shape3d.cs, Cuboid3d.cs, Quaternion.cs and Camera.cs. This library uses the right handed rectangular coordinate system and has the same X, Y coordinates as GDI+:
About the Program
To illustrate how this libray works, I wrote this program. When you run this program, a colored cube is loaded, and its center is shown with the camera's position in pixels. Their rotated degrees are set as zero. This program is quite intuitive. You can have pictures on each of the cube surfaces by clicking button Load Image. You can also reset this program by button Reset. Just a reminder: because rotation sequence is incommutable, it's possible that the cube is not in its initial state when all the rotated degrees are returned to zeros.
About the Code
Quaternion
In mathematics, quaternions are a non-commutative number system that extend the complex numbers. They provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Quaternions have 4 dimensions (each quaternion consists of 4 scalar numbers), one real dimension w and 3 imaginary dimensions xi + yj + zk that can describe an axis of rotation and an angle. Quaternions are often used in 3D engines to rotate points in space quickly.
Define the quaternion:
q = w + xi + yj + zk = w + (x, y, z) = cos(a/2) + usin(a/2)
where u is a unit vector and a is rotated angle around the u axis.
Let also v be an ordinary vector of the 3 dimensional space, considered as a quaternion with a real coordinate equal(w) to zero. Then the quaternion product:
qvq-1
yields the vector v rotated by an angle a around the u axis. The rotation is clockwise if our line of sight points in the direction pointed by u. This operation is known as conjugation by q. The quaternion multiplication is composition of rotations, for if p and q are quaternions representing rotations, then rotation (conjugation) by pq is:
pqv(pq)-1 = pqvp-1p-1 = p(qvq-1)p-1
Let's look at the construction of Quaternion.cs:
public struct Quaternion
{
public double X, Y, Z, W;
public Quaternion(double w, double x, double y, double z)
{
W = w; X = x; Y = y; Z = z;
}
public Quaternion(double w, Vector3d v)
{
W = w; X = v.X; Y = v.Y; Z = v.Z;
}
public void FromAxisAngle(Vector3d axis, double angleRadian)
{
double m = axis.Magnitude;
if (m > 0.0001)
{
double ca = Math.Cos(angleRadian / 2);
double sa = Math.Sin(angleRadian / 2);
X = axis.X / m * sa;
Y = axis.Y / m * sa;
Z = axis.Z / m * sa;
W = ca;
}
else
{
W = 1; X = 0; Y = 0; Z = 0;
}
}
... ...
multiplication of quaternion q1 with q2 is:
(w1 + x1i + y1j + z1k)*(w2 + x2i + y2j + z2k)
and
i*j = k, j*k = i, k*i = j; i*i = -1, j*j = -1, k*k = -1
So we can easily obtain this code based on the above information:
public static Quaternion operator *(Quaternion q1, Quaternion q2)
{
double nw = q1.W * q2.W - q1.X * q2.X - q1.Y * q2.Y - q1.Z * q2.Z;
double nx = q1.W * q2.X + q1.X * q2.W + q1.Y * q2.Z - q1.Z * q2.Y;
double ny = q1.W * q2.Y + q1.Y * q2.W + q1.Z * q2.X - q1.X * q2.Z;
double nz = q1.W * q2.Z + q1.Z * q2.W + q1.X * q2.Y - q1.Y * q2.X;
return new Quaternion(nw, nx, ny, nz);
}
The code for the rotation by quaternion follows:
public void Rotate(Point3d pt)
{
this.Normalise();
Quaternion q1 = this.Copy();
q1.Conjugate();
Quaternion qNode = new Quaternion(0, pt.X, pt.Y, pt.Z);
qNode = this * qNode * q1;
pt.X = qNode.X;
pt.Y = qNode.Y;
pt.Z = qNode.Z;
}
public void Rotate(Point3d[] nodes)
{
this.Normalise();
Quaternion q1 = this.Copy();
q1.Conjugate();
for (int i = 0; i < nodes.Length; i++)
{
Quaternion qNode = new Quaternion(0, nodes[i].X, nodes[i].Y, nodes[i].Z);
qNode = this * qNode * q1;
nodes[i].X = qNode.X;
nodes[i].Y = qNode.Y;
nodes[i].Z = qNode.Z;
}
}
Camera
Since the computer monitor is limited to displaying 2D images, we have to flatten the 3D objects on to the 2D plane using projection. Camera.cs is used to transform the 3D point to 2D point on the plane. Camera.cs has three properties:
public class Camera
{
Point3d loc = new Point3d(0, 0, 0);
double _d = 500.0;
Quaternion quan = new Quaternion(1, 0, 0, 0);
public Point3d Location
{
set { loc = value; }
get { return loc; }
}
public double FocalDistance
{
set { _d = value; }
get { return _d; }
}
public Quaternion Quaternion
{
set { quan = value; }
get { return quan; }
}
... ...
When the camera moves, its Location is changed:
public void MoveRight(double d)
{
loc.X += d;
}
public void MoveLeft(double d)
{
loc.X -= d;
}
public void MoveUp(double d)
{
loc.Y -= d;
}
public void MoveDown(double d)
{
loc.Y += d;
}
public void MoveIn(double d)
{
loc.Z += d;
}
public void MoveOut(double d)
{
loc.Z -= d;
}
And when camera turns, the Quaternion records the rotation of camera:
public void Roll(int degree) // rotate around Z axis
{
Quaternion q = new Quaternion();
q.FromAxisAngle(new Vector3d(0, 0, 1), degree * Math.PI / 180.0);
quan = q * quan;
}
public void Yaw(int degree) // rotate around Y axis
{
Quaternion q = new Quaternion();
q.FromAxisAngle(new Vector3d(0, 1, 0), degree * Math.PI / 180.0);
quan = q * quan;
}
public void Pitch(int degree) // rotate around X axis
{
Quaternion q = new Quaternion();
q.FromAxisAngle(new Vector3d(1, 0, 0), degree * Math.PI / 180.0);
quan = q * quan;
}
public void TurnUp(int degree)
{
Pitch(-degree);
}
public void TurnDown(int degree)
{
Pitch(degree);
}
public void TurnLeft(int degree)
{
Yaw(degree);
}
public void TurnRight(int degree)
{
Yaw(-degree);
}
To project the 3D point to 2D, the first step is to translate the origin to the camera's Location and use camera's Quaternion to rotate the 3D objects in relation to camera's rotation. The second step is projection:
public PointF[] GetProjection(Point3d[] pts)
{
PointF[] pt2ds = new PointF[pts.Length];
// transform to new coordinates system which origin is camera location
Point3d[] pts1 = Point3d.Copy(pts);
Point3d.Offset(pts1, -loc.X, -loc.Y, -loc.Z);
// rotate
quan.Rotate(pts1);
//project
for (int i = 0; i < pts.Length; i++)
{
if (pts1[i].Z > 0.1)
{
pt2ds[i] = new PointF((float)(loc.X + pts1[i].X * _d / pts1[i].Z),
(float)(loc.Y + pts1[i].Y * _d / pts1[i].Z));
}
else
{
pt2ds[i] = new PointF(float.MaxValue, float.MaxValue);
}
}
return pt2ds;
}
}
3D Object and Cube
Shape3d.cs is a primitive base class that records the key 3D points for drawing shape and provides the abilities to draw 3D shapes:
public class Shape3d
{
protected Point3d[] pts = new Point3d[8];
public Point3d[] Point3dArray
{
get { return pts; }
}
protected Point3d center = new Point3d(0, 0, 0);
public Point3d Center
{
set
{
double dx = value.X - center.X;
double dy = value.Y - center.Y;
double dz = value.Z - center.Z;
Point3d.Offset(pts, dx, dy, dz);
center = value;
}
get { return center; }
}
protected Color lineColor = Color.Black;
public Color LineColor
{
set { lineColor = value; }
get { return lineColor; }
}
public void RotateAt(Point3d pt, Quaternion q)
{
// transform origin to pt
Point3d[] copy = Point3d.Copy(pts);
Point3d.Offset(copy, - pt.X, - pt.Y, - pt.Z);
// rotate
q.Rotate(copy);
q.Rotate(center);
// transform to original origin
Point3d.Offset(copy, pt.X, pt.Y, pt.Z);
pts = copy;
}
public virtual void Draw(Graphics g,Camera cam)
{
}
}
Now it's possible to construct any 3D object. Here's a simple example, Cuboid derived from Shape3d.cs:
public Cuboid(double a, double b, double c)
{
center = new Point3d(a / 2, b / 2, c / 2);
pts[0] = new Point3d(0, 0, 0);
pts[1] = new Point3d(a, 0, 0);
pts[2] = new Point3d(a, b, 0);
pts[3] = new Point3d(0, b, 0);
pts[4] = new Point3d(0, 0, c);
pts[5] = new Point3d(a, 0, c);
pts[6] = new Point3d(a, b, c);
pts[7] = new Point3d(0, b, c);
}
To draw the 3D cube on screen, we have to pass its 3D points to Camera.cs and get the 2D points for drawing:
public override void Draw(Graphics g, Camera cam)
{
PointF[] pts2d = cam.GetProjection(pts);
... ...
You can also fill the cube face; however, you can only fill the fore face and not the back face. So we have to identify which is the fore face:
if (YLScsDrawing.Geometry.Vector.IsClockwise(face[i][0], face[i][1], face[i][2]))
// the face can be seen by camera
{
if (fillingFace) g.FillPolygon(new SolidBrush(faceColor[i]), face[i]);
... ...
To have some fun, I placed the pictures on the fore face by Free Image Transformation:
if (drawingImage && bmp[i] != null)
{
filters[i].FourCorners = face[i];
g.DrawImage(filters[i].Bitmap, filters[i].ImageLocation);
}
Thanks
Thanks a lot for reading and have fun trying out my 3D Library.
History
- 1st June, 2009: Initial post
