Particle swarm optimization for function optimization
4.86/5 (31 votes)
A particle swarm can be used to optimize functions. To do so, the particles explore the search space and try to find the minimum or maximum of a given function.
Introduction
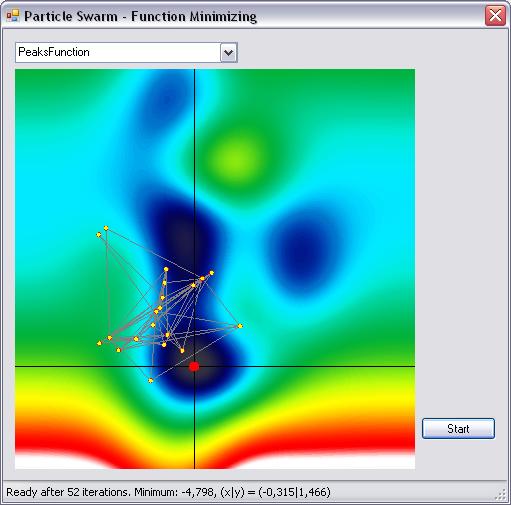
Particle swarm optimization (PSO) is a population based stochastic optimization technique developed by Dr. Eberhart and Dr. Kennedy in 1995, inspired by the social behavior of birds. The algorithm is very simple but powerful. Here, I'm going to show how PSO can be used to minimize functions. Thus, PSO can be used as a training method for artificial neural networks or to minimize/maximize other high dimensional functions. In the example shown, a function R² -> R is minimized. Videos of the exploration by "virtual birds" can be watched at YouTube:
Background
To understand the algorithm, it is best to imagine a swarm of birds that are searching for food in a defined area - there is only one piece of food in this area. Initially, the birds don't know where the food is, but they know at each time how far the food is. Which strategy will the birds follow? Well, each bird will follow the one that is nearest to the food.
PSO adapts this behaviour and searches for the best solution-vector in the search space. A single solution is called particle. Each particle has a fitness/cost value that is evaluated by the function to be minimized, and each particle has a velocity that directs the "flying" of the particles. The particles fly through the search space by following the optimum particles.
The algorithm is initialized with particles at random positions, and then it explores the search space to find better solutions. In every iteration, each particle adjusts its velocity to follow two best solutions. The first is the cognitive part, where the particle follows its own best solution found so far. This is the solution that produces the lowest cost (has the highest fitness). This value is called pBest (particle best). The other best value is the current best solution of the swarm, i.e., the best solution by any particle in the swarm. This value is called gBest (global best). Then, each particle adjusts its velocity and position with the following equations:
v' = v + c1.r1.(pBest - x) + c2.r2.(gBest - x)
x' = x + v'
v is the current velocity, v' the new velocity, x the current position, x' the new position, pBest and gBest as stated above, r1 and r2 are even distributed random numbers in the interval [0, 1], and c1 and c2 are acceleration coefficients. Where c1 is the factor that influences the cognitive behaviour, i.e., how much the particle will follow its own best solution, and c2 is the factor for social behaviour, i.e., how much the particle will follow the swarm's best solution.
The algorithm can be written as follows:
- Initialize each particle with a random velocity and random position.
- Calculate the cost for each particle. If the current cost is lower than the best value so far, remember this position (pBest).
- Choose the particle with the lowest cost of all particles. The position of this particle is gBest.
- Calculate, for each particle, the new velocity and position according to the above equations.
- Repeat steps 2-4 until maximum iteration or minimum error criteria is not attained.
It's quite a simple algorithm, but very powerful. This is the kind of algorithm that catches my fascination.
Implementation

Abstract implementation
The code does nothing more than what was stated in the above algorithm. At first, I'll show the abstract implementation of the particle swarm and the particles. For brevity, the properties are omitted, they can be seen in the above class diagram (or in the attached source). The concrete implementation for minimizing the function is shown afterwards.
Particle swarm
public abstract class ParticleSwarm
{
...
//---------------------------------------------------------------------
#region Methoden
/// <summary>
/// Sorts the particles according their cost.
/// </summary>
public void SortParticles()
{
Array.Sort(this.Particles);
}
//---------------------------------------------------------------------
/// <summary>
/// Does one iteration of the algorithm.
/// </summary>
public virtual void Iteration()
{
// Foreach particle calculate the cost and update the history:
var localParticles = this.Particles; // Range-Check-Elimination
for (int i = 0; i < localParticles.Length; i++)
{
localParticles[i].CalculateCost();
localParticles[i].UpdateHistory();
}
// Sort according to fitness:
this.SortParticles();
// Update history of the swarm:
if (this.Cost < this.BestCost)
{
this.BestCost = this.Cost;
this.BestPosition = this[0].BestPosition;
}
// Determine new velocity and position of the particles in
// the swarm:
for (int i = 0; i < localParticles.Length; i++)
if (_useGlobalOptimum)
localParticles[i].UpdateVelocityAndPosition(BestPosition);
else
localParticles[i].UpdateVelocityAndPosition(this[0].Position);
}
#endregion
...
}
Particle
public abstract class Particle : IComparable<particle>
{
...
/// <summary>
/// Calculates the cost for this particle.
/// </summary>
public abstract void CalculateCost();
//---------------------------------------------------------------------
/// <summary>
/// Updates the history for this particle.
/// </summary>
public void UpdateHistory()
{
if (this.Cost < _bestCost)
{
_bestCost = this.Cost;
this.BestPosition = this.GetArrayCopy();
}
}
//---------------------------------------------------------------------
/// <summary>
/// Updates the position (and velocity) of the particle.
/// </summary>
/// <param name=""bestPositionOfSwarm"" />
/// The current best position of the particle swarm.
///
public void UpdateVelocityAndPosition(double[] bestPositionOfSwarm)
{
if (this.BestPosition == null)
this.UpdateHistory();
// Determine maximum allowed velocity:
double xmax = Math.Max(
Math.Abs(this.Position.Min()),
Math.Abs(this.Position.Max()));
double vmax = this.Swarm.PercentMaximumVelocityOfSearchSpace * xmax;
// Range-Check-Elimination: Therefore get a reference to the arrays
// on the local stack -> improvement of speed:
double[] localVelocity = this.Velocity;
double[] localPosition = this.Position;
double[] localBestPosition = this.BestPosition;
for (int i = 0; i < localVelocity.Length; i++)
{
// Factors for calculating the velocity:
double c1 = this.Swarm.TendencyToOwnBest;
double r1 = _rnd.NextDouble();
double c2 = this.Swarm.TendencyToGlobalBest;
double r2 = _rnd.NextDouble();
double m = this.Swarm.Momentum;
// New velocity of the particle:
double newVelocity =
m * localVelocity[i] +
c1 * r1 * (localBestPosition[i] - localPosition[i]) +
c2 * r2 * (bestPositionOfSwarm[i] - localPosition[i]);
// Limit the velocity to the maximum value:
if (newVelocity > vmax)
newVelocity = vmax;
if (newVelocity < -vmax)
newVelocity = -vmax;
// Assign new velocity and calculate the new position:
localVelocity[i] = newVelocity;
localPosition[i] += localVelocity[i];
}
}
...
}
Concrete implementation for minimizing functions
Particle swarm for minimizing functions
public sealed class FunctionMinimizingParticleSwarm : ParticleSwarm
{
public FunctionMinimizingParticleSwarm(
FunctionBase function,
int swarmSize)
{
// Create the swarm:
this.InitSwarm(swarmSize, function);
// Sort according to the cost of each particle:
this.SortParticles();
}
//---------------------------------------------------------------------
public void InitSwarm(int swarmSize, FunctionBase function)
{
// Create the array of particles:
this.Particles = new FunctionMinimizingParticle[swarmSize];
for (int i = 0; i < swarmSize; i++)
{
// Init with random position in [-3,3]:
double x = _rnd.NextDouble() * 6 - 3;
double y = _rnd.NextDouble() * 6 - 3;
double[] particlePosition = { x, y };
// Random initial velocity [-3,3]:
double vx = _rnd.NextDouble() * 6 - 3;
double vy = _rnd.NextDouble() * 6 - 3;
double[] particleVelocity = { vx, vy };
this[i] = new FunctionMinimizingParticle(
function,
this,
particlePosition,
particleVelocity);
}
}
}
The concrete particle
public sealed class FunctionMinimizingParticle : Particle
{
private FunctionBase _function;
//---------------------------------------------------------------------
public FunctionMinimizingParticle(
FunctionBase function,
ParticleSwarm swarm,
double[] position,
double[] velocity)
{
_function = function;
this.Swarm = swarm;
this.Position = position;
this.Velocity = velocity;
this.CalculateCost();
}
//---------------------------------------------------------------------
public override void CalculateCost()
{
this.Cost = _function.Function(this.Position);
}
}
Well, that was the whole magic of particle swarm optimization.
How to use?
To use these classes, quite a few lines of code are needed.
...
private FunctionMinimizingParticleSwarm _swarm;
...
_swarm = new FunctionMinimizingParticleSwarm(_function, SWARM_SIZE);
...
double minimum = double.MaxValue;
double oldMinimum = double.MinValue;
int countSame = 0;
...
// Wait for 25 iteration without any improvement:
while (countSame < 25)
{
_swarm.Iteration();
minimum = _swarm.BestCost;
if (Math.Abs(oldMinimum - minimum) < 0.001)
{
countSame++;
oldMinimum = minimum;
_bestSolution = _swarm.BestPosition;
}
else
{
countSame = 0;
oldMinimum = minimum;
}
}
...
The full example for minimizing the function R² -> R is attached. It's basically the same code that was used to create the plot view video.
Points of interest
The "Particle swarm optimization" algorithm is quite similar to genetic algorithms and can be used for similar problems. I found out that PSO is quite good in training feedforward neural networks. The algorithm allows for parallelization which can boost the execution speed. A swarm size of 50 is sufficient in most cases, and therefore the algorithm uses less resources compared to a genetic algorithm (where the population can be 1000+).
Have a look at my blog for some additional information on other meta heuristic algorithms.
History
- 10 September 2009: Initial release.
